Алгоритмы на графах
Теория: Классы сложности алгоритмов и задач
В обычной жизни мы называем задачу сложной, если ее трудно решить. Но для программистов это работает не так: у них сложность задачи определяется сложностью алгоритма, который ее решает. В этом уроке мы подробнее познакомимся с термином «сложность» и узнаем, как классифицировать задачи по этому признаку.
Как работает сложность в теории алгоритмов
Чтобы компьютеры справлялись со сложными задачами, производители постоянно наращивают вычислительные мощности компьютерного железа. Например, современные процессоры уже могут выполнять миллион миллионов операций в секунду.
Такие эффективные процессоры справляются даже с непростыми задачами. Для примера вспомним алгоритм перемножения матриц размером в n. Сложность этого алгоритма высокая — O(n^3). Несмотря на это, процесс сработает мгновенно — за тысячную долю секунды, даже если мы нужно перемножить матрицы размером 1000 * 1000.
В базовом курсе по алгоритмам мы познакомились с несколькими алгоритмическими сложностями. Некоторые из них показаны в таблице:
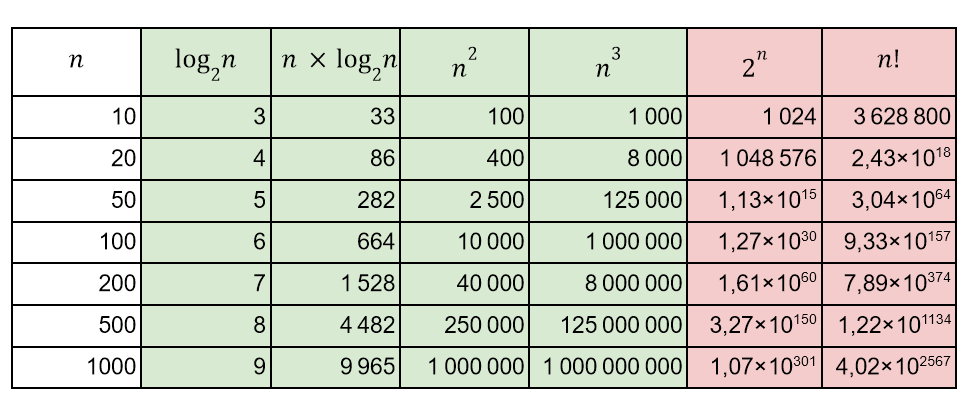
Алгоритмы из левой части таблицы выполняются быстро, поэтому они называются простыми*. В последних двух столбцах таблицы мы видим долгие алгоритмы — они сложные.
Возьмем для примера уже известную нам задачу о рюкзаке, которая решается перебором. Для n предметов она выполняется за время O(2^n).
Существуют ли более быстрые решения? В строгом смысле — нет:
- Есть быстрые алгоритмы, которые находят хорошее, но не обязательно оптимальное решение
- Есть метод ветвей и границ, который оптимизирует перебор и отбрасывают заведомо плохие варианты, но его эффективность не гарантирована. В худшем случае он сработает за время
O(2^n)
Функция 2^n — экспоненциальная, поэтому сложность алгоритма и сложность задачи о рюкзаке также считаются экспоненциальными.
Другими словами, с количеством предметов радикально меняется и скорость выполнения алгоритма. Чтобы собрать рюкзак из пятидесяти предметов, потребуется двадцать минут, а из ста предметов — сорок миллиардов лет.
В реальной жизни речь идет не об абстрактном рюкзаке. Например, это может быть грузовой контейнер, куда помещаются сотни ящиков. Очевидно, что невозможно подобрать оптимальный груз для такого контейнера за приемлемое время.
На практике, различия в сложности алгоритмов не так существенны — важнее, в какую половину таблицы они попали. Вернемся к нашей таблице:
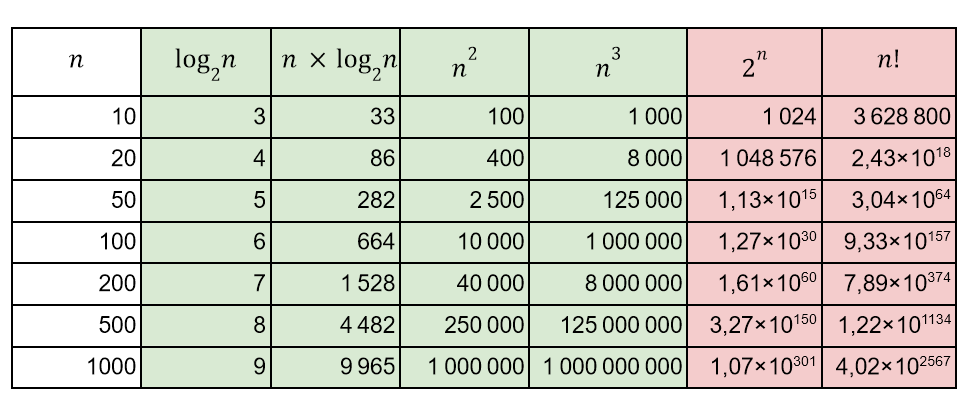
Большинство востребованных алгоритмов можно разбить на две большие группы или два больших класса:
- Если задача решается алгоритмами из зеленой зоны, то она относится к классу сложности P — это сокращение от polynomial (полиномиальные, они же степенные)
- Если задача решается алгоритмами из красной зоны, то она относится к классу сложности NP — это сокращение от nondeterministic polynomial (недетерминированные полиномиальные)
К классу P относятся задачи не только со степенными, но и с более быстрыми алгоритмами — логарифмическими, линейными и линейно-логарифмическими. Название класса не следует понимать буквально. Оно означает, что для решения задачи существует достаточно быстрый алгоритм — не хуже полиномиального.
Недетерминированные полиномиальные задачи
В наших уроках мы избегаем сложной математики. Это связано с тем, что программирование — инженерная деятельность. Чтобы писать программы, программист должен владеть определенными методами, но ему необязательно придумывать эти методы и доказывать их корректность.
В то же время, математики разрабатывают методы и алгоритмы, поэтому они обязаны предоставлять доказательства их правильности. Часто такие доказательства — это рассуждения о работе алгоритма на вычислительной машине.
Реальный компьютер — это сложное устройство. Поэтому и рассуждения о деталях его работы тоже оказываются слишком сложными. Чтобы их упростить, математики отбрасывают все несущественные детали. Например, они считают, что у компьютера всегда хватает оперативной памяти. Такие гипотетические упрощенные вычислительные машины называют абстрактными.
Самая известная абстракция — недетерминированная машина Тьюринга. С ее помощью доказано большинство утверждений об алгоритмах и вычислениях.
От обычного компьютера машина Тьюринга отличается только по одному параметру — у нее неограниченный запас процессоров и неограниченная оперативная память.
Из-за этого машина Тьюринга очень быстрая — большинство алгоритмов с экспоненциальной и факториальной сложностью она выполняет за полиномиальное время. К сожалению, в реальности такой машины не существует — математики придумали ее, чтобы рассуждать об алгоритмах.
Формальное определение гласит:
К классу NP относятся все задачи, которые можно решить за полиномиальное время на недетерменированной машине Тьюринга
Если не углубляться в теорию алгоритмов, это определение кажется странным. Судя по этому определению, мы должны писать программы для несуществующих компьютеров и доказывать, что вычисления в них выполняются достаточно быстро.
Однако у NP-задач есть и менее абстрактная формулировка.
Задачи разрешимости
Во многих задачах этого курса мы искали заранее неизвестный ответ. Решая эти задачи, мы получали путь в графе, набор предметов для рюкзака или список городов для коммивояжера.
Но есть и другие задачи, например: «Совпадают ли две строки символов или является массив отсортированным?». У подобных задач только два варианта решения — «да» или «нет». Такие задачи называют задачами разрешимости.
Обычно задачи разрешимости решаются проще, чем задачи с произвольным ответом. Проверка известного решения тоже относится к таким задачам, поэтому их иногда называют задачами верификации.
Представим, у нас есть карта с городами и расстояниями между ними. Нам говорят, что коммивояжер может объехать все города и суммарный путь не превысит 400 километров. Чтобы проверить это утверждение, нужно решить задачу коммивояжера, что требует факториального времени.
Теперь представим, что нам не только выдали карту, но и показали конкретный маршрут. Сложно ли решить такую задачу? Совсем нет. Мы всего лишь должны проверить несколько фактов:
- В маршрут входят все города
- Города появляются не более одного раза
- Сумма всех расстояний между городами не превышает
400
Самая алгоритмически сложная задача здесь — поиск дубликатов в списке городов. Даже если мы используем простейший алгоритм попарного сравнения, мы решим ее за время O(n^2).
Таким образом, мы приходим к еще одному определению:
К классу NP относятся задачи, решение которых можно проверить за полиномиальное время на детерминированной машине Тьюринга — то есть на обычном компьютере
Это определение не такое абстрактное, как предыдущее. По крайней мере, для проверки задач не требуется вымышленная машина — достаточно обычного компьютера.
В обоих определениях есть одна странность — задачи класса P входят в класс NP. Это сбивает с толку. Мы хотели различать задачи и ввели классы сложности, а теперь выясняется, что простые задачи относятся и к сложным.
На самом деле, противоречия нет.
Первая причина в том, что как речь идет о худшем случае, как в задачах класса P. Если задача решается за полиномиальное время, то и проверка решения займет полиномиальное время, даже в худшем случае. Но есть еще и вторая причина.
Основная проблема теории алгоритмов
Удивительный факт: мы не знаем, различаются ли классы P и NP на самом деле. Для задачи о рюкзаке или о коммивояжере известны только медленные переборные алгоритмы. Еще никто не доказал, что более быстрых алгоритмов не существует.
Такие доказательства возможны. Например, даже в самом быстром алгоритме сортировки количество сравнений не может быть меньше O(N * logN). Это значит, что в общем случае сортировка не может быть быстрее, чем O(N * logN)^2.
При этом программисты постоянно улучшают существующие алгоритмы. Например, для алгоритма сортировки сначала были известны только решения O(N^2), поэтому гипотетически у задачи о рюкзаке может найтись и полиномиальное решение. Если оно существует, для многих практических задач мы сможем гарантированно находить оптимальное решение. Это поможет эффективно заполнять грузовые контейнеры или составлять школьные расписания.
Впрочем, за последние 50 лет не появилось ни одного быстрого алгоритма для задач класса NP. Проблема равенства или не равенства классов P и NP важна настолько, что ее называют основной проблемой теории алгоритмов или одной из задач тысячелетия.
Дело даже не в том, что мы сможем быстро решать практические задачи. Оказывается, что существует класс задач, которые называют NP-полными. Если мы найдем быстрый алгоритм для любой из них, то сможем придумать быстрый алгоритм для любой NP-задачи. Разберемся, почему это так.
NP-полные задачи
Далеко не всегда нам приходиться решать задачи с нуля. Многие из них можно свести друг к другу и сэкономить время на поиск алгоритма. Ранее в курсе мы обсуждали задачу о монетах и минимальной сдаче. По сути, это частный случай задачи о рюкзаке, поэтому для ее решения можно взять готовый жадный алгоритм.
Кажется, что сводить другу к другу можно именно похожие задачи, но это не всегда так. Выше мы уже обсуждали недетерминированные машины Тьюринга и их важность для доказательств. В 1971 году американскому математику Стивену Куку удалось доказать, что все задачи из класса NP можно свести к задаче о выполнимости, которая в научных кругах называется SAT (от английского satisfiability — выполнимость).
Представим, что у нас есть логическая формула. На языке JavaScript это формула состоит из:
- Скобок
- Логических переменных со значением
trueиfalse - Логических операторов:
&&(И)||(ИЛИ)!(НЕ)
Примером такой формулы служит a && b || !c.
В задаче о выполнимости нужно узнать, при каких значениях a, b и c эта формула будет выполняться. Задача решается методом перебора. Для выражения из n переменных необходимо перебрать 2^n вариантов, то есть речь идет об экспоненциальном алгоритме.
Стивен Кук доказал, что мы можем свести к решению SAT любую программу для недетерминированной машины Тьюринга, которая работает за полиномиальное время. Это утверждение звучит немного абстрактно, но из него следует важный вывод. Если мы найдем быстрое решение для SAT, то найдем и решение для любой задачи из класса NP, включая задачу о рюкзаке и коммивояжере.
SAT стала первой, но не единственной NP-полной задачей. Если мы можем свести SAT к другой задаче из класса NP, она также становится NP-полной. Сейчас известны десятки NP-полных задач, включая задачу о рюкзаке и коммивояжере. Если нам удастся найти быстрый алгоритм для любой NP-полной задачи, мы автоматически получим быстрые алгоритмы для всех NP-задач.
Если мы выясним, что классы P и NP эквивалентны, это будет хорошим подарком человечеству. Но нас ждут и негативные последствия. Дело в том, что вся криптография с открытым ключом построена на предположении, что некоторые NP-задачи сложны.
Для примера возьмем алгоритм шифрования RAS. Чтобы расшифровать данные, нужно решить задачу о разбиение числа на простые множители. Она выполняется за экспоненциальное время — то есть на решение уйдет очень много времени, поэтому алгоритм и считается надежным способом шифрования. Но если мы найдем полиномиальный алгоритм, шифрование RAS перестанет работать: злоумышленники смогут без труда подделывать цифровые подписи и сертификаты безопасности.
А из-за теоремы Кука это обязательно случится, если мы обнаружим полиномиальный алгоритм для любой NP-полной задачи. Учитывая количество открытых NP-полных задач, можно предположить, что вероятность такого события достаточно высока.
Но на самом деле большая часть научного сообщества считает, что классы P и NP все-таки различаются, так что мы никогда не придумаем быстрого алгоритма составления расписаний. Может показаться, что это очень плохо, но все не так просто.
В следующем уроке мы обсудим эвристические алгоритмы, которые позволяют находить пусть не оптимальные, но достаточно хорошие решения.
Выводы
Повторим ключевые мысли этого урока:
- В теории алгоритмов быстрые алгоритмы называют простыми, а медленные — сложными
- Сложными называют задачи, для которых не существует быстрого решения
- Большинство задач относятся к одному из классов сложности — P или NP
- Задачи из класса P решаются за полиномиальное время в худшем случае
- Задачи из класса NP проверяются за полиномиальное время в худшем случае
- До сих пор неизвестно, эквивалентны ли классы P и NP
- Если они эквивалентны, мы сможем составлять оптимальные расписания и строить оптимальные маршруты, но лишимся асимметричных методов шифрования, на которых работает весь интернет
- Существует класс NP-полных задач, к которым сводится любая NP-задача
- Если мы найдем быстрый алгоритм решения любой NP-полной задачи, мы сможем быстро решать все NP-задачи — тогда гипотеза об эквивалентности P и NP будет доказана
- Научное сообщество в большинстве своем считает, что классы P и NP не эквивалентны

