В этом и других курсах вы могли сталкиваться с различными учебными проектами. Обычно они достаточно реалистичные, но одно различие все таки есть — все учебные проекты небольшие.
Реальные проекты намного больше учебных. Чтобы разработчики не путались в коде, обычно большие проекты состоят из отдельных пакетов. При этом появляются зависимости.
Например, если пакет А импортирует или использует пакет Б, мы говорим: «А зависит от Б». На схеме эту зависимость можно обозначить так:
Чтобы собрать проект, нам нужно загружать или компилировать пакеты в правильном порядке. Если А зависит от Б, то сначала надо загрузить пакет Б, и только потом перейти к пакету А.
Когда пакетов в проекте много, количество зависимостей тоже растет. Вместе они образуют сложный граф зависимостей:
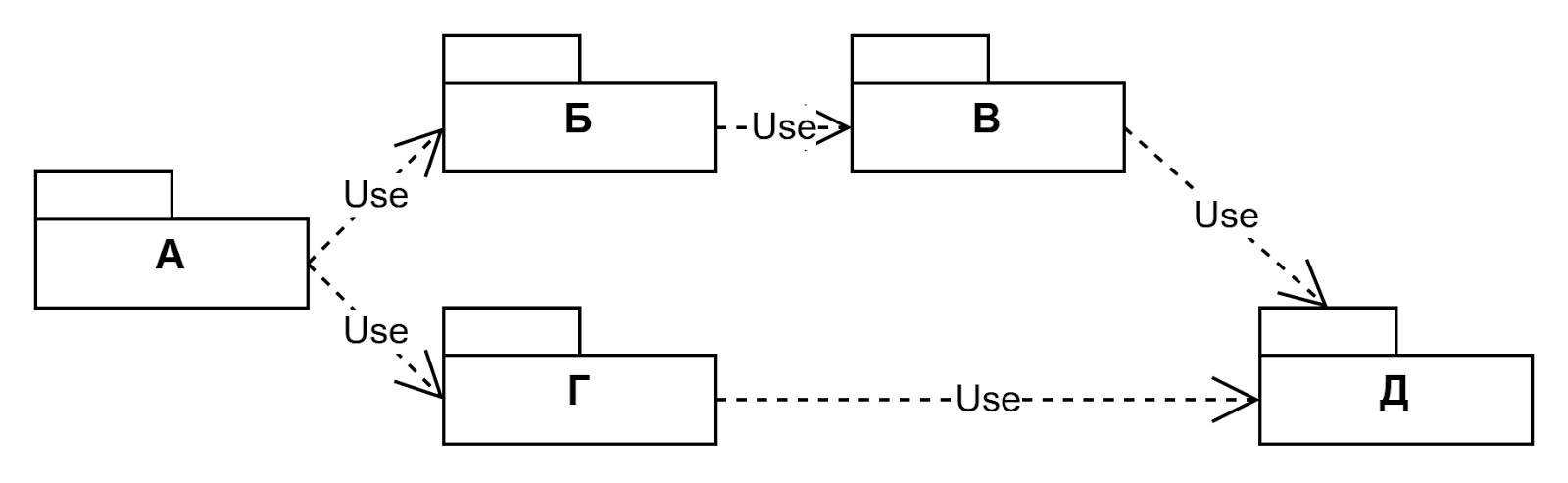
Пакеты из этого графа можно загружать или компилировать в правильном порядке. Судя по графу, возможно три варианта:
-
Д, Б, В, Г, А
-
Д, Г, В, Б, А
-
Д, В, Г, Б, А
У нас есть выбор, потому что ветки Г и Б + В не зависят друг от друга. В любом случае первым пакетом следует Д, потому что он ни от кого не зависит. Последним идет пакет А, потому что от него никто не зависит.
Подобная структура зависимостей часто встречается в программировании. Например, таким образом мы описываем связи между классами, которые задействованы в коде. Это называется внедрение зависимостей (Dependency Injection).
Но есть проблема — часто программисты не описывают граф целиком, а только указывают, от каких узлов зависит очередной узел.
Это приводит к тому, что в графе может появиться циклическая зависимость:
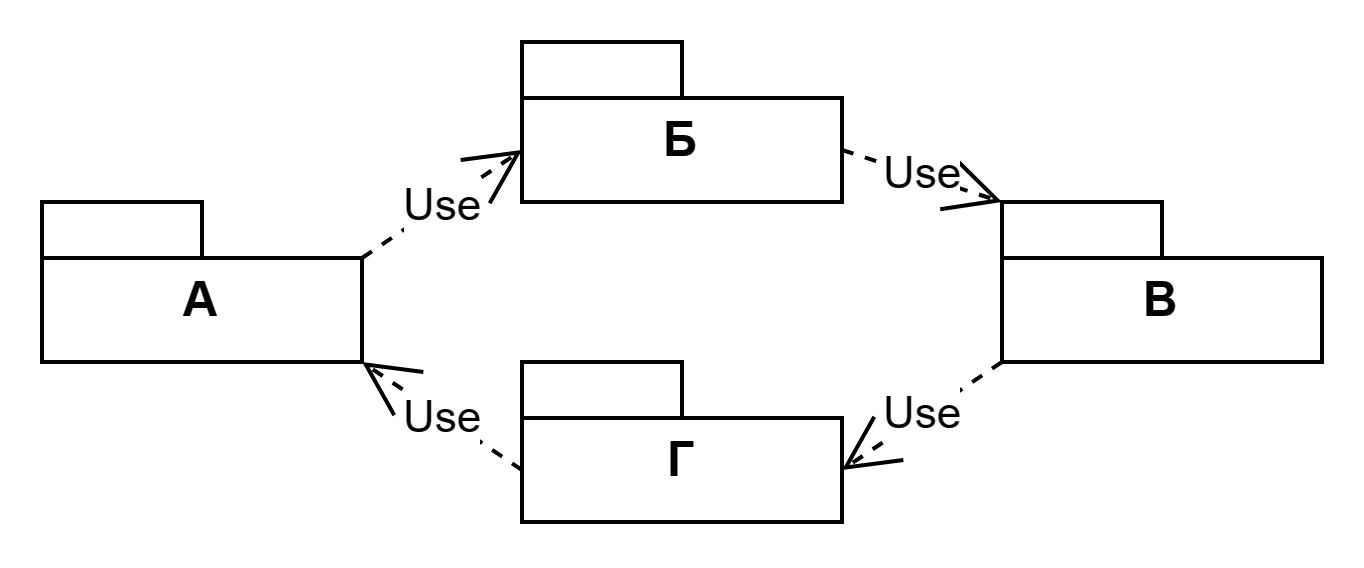
В циклическом графе невозможно определить правильный порядок компиляции пакетов или создания объектов. Справиться с этой сложностью помогают системы сборки и библиотеки внедрения зависимостей. Именно благодаря им программисты находят циклы в описанных графах.
В этом уроке мы научимся искать циклы в ориентированных графах. Задача для неориентированных графов на практике встречается гораздо реже, поэтому мы не станем обсуждать ее подробно. Она решается похожим образом, так что алгоритм можно без труда адаптировать.
Матрица смежности
В прошлых уроках мы познакомились с двумя способами представления графов:
-
Со списками смежности
-
С неявным представлением
Сегодня изучим матрицу смежности — еще одну структуру данных, которую часто применяют при работе с графами.
Все вершины графа мы храним в массиве, так что у каждой вершины появляется уникальный порядковый номер. В большинстве современных языков программирования нумерация элементов начинается с ноля. Поэтому у нас будут вершина , вершина , вершина и так далее:
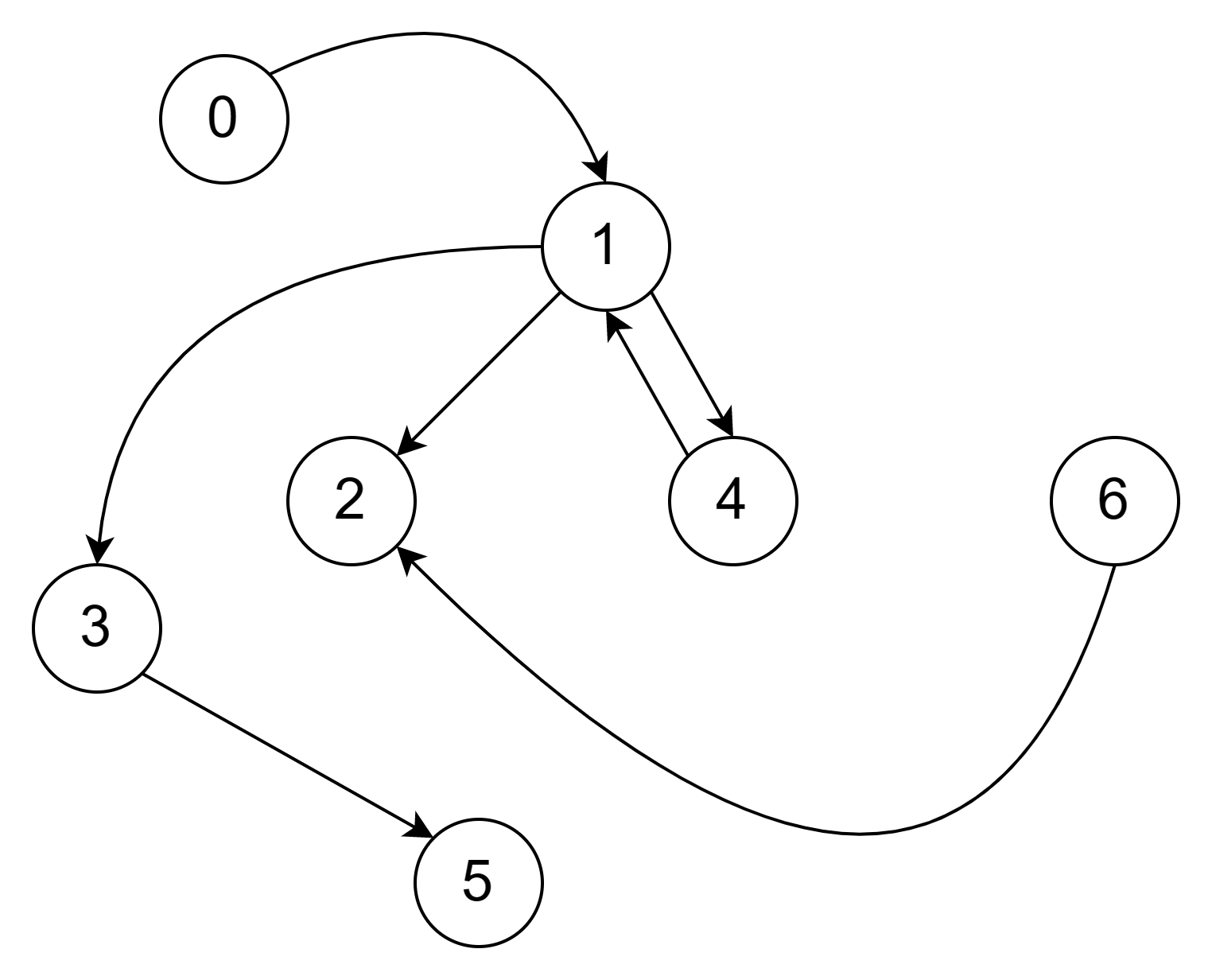
Важно, что номера вершин идут подряд без пропусков.
Вместе с массивом мы храним матрицу — двумерный массив. Ее ширина и высота равны количеству вершин. Есть речь идет об обычном невзвешенном графе, элементами массива будут:
-
Либо булевы значения — и
-
Либо числа и
Вернемся к рисунку выше. На нем мы видим, какие вершины связаны между собой. Эту информацию мы можем записать в матрицу смежности. Помните, что нумерация вершин начинается с 0, поэтому нумерация столбцов и строк сдвигается на единицу.
-
На графе вершина связана с вершиной — записываем в строку и столбец :
-
На графе вершина не связана с вершиной — записываем в строку и столбец :
Перебирая элементы строки, мы можем найти все связанные вершины.
Во взвешенном графе вместо булевых значений мы можем хранить числа:
-
Если вершины не связаны —
-
Если вершины связаны — число, обозначающее вес ребра
Матрица смежности подходит для хранения ориентированных графов. Для хранения неориентированных графов программисты используют небольшой трюк, делая матрицу симметричной. Для примера представим, что мы хотим связать вершины и . В этом случае мы записываем два раза:
-
В столбец и строку
-
В столбец и строку
Так мы получаем двустороннюю связь.
Поиск цикла
Обычно нам надо убедиться, что в графе нет циклов. Поэтому мы пытаемся найти хотя бы один любой цикл. Если нам это удается, то мы подсказываем пользователю, из каких вершин он состоит.
Оказывается, для поиска циклов не надо изобретать нового алгоритма — можно адаптировать обход графа в глубину. При обходе мы будем помечать посещенные вершины. В реальной программе каждой вершине будет приписан числовой код, но при объяснении алгоритма принято говорить о «перекрашивании» вершин.
Попробуем найти цикл в таком небольшом графе:
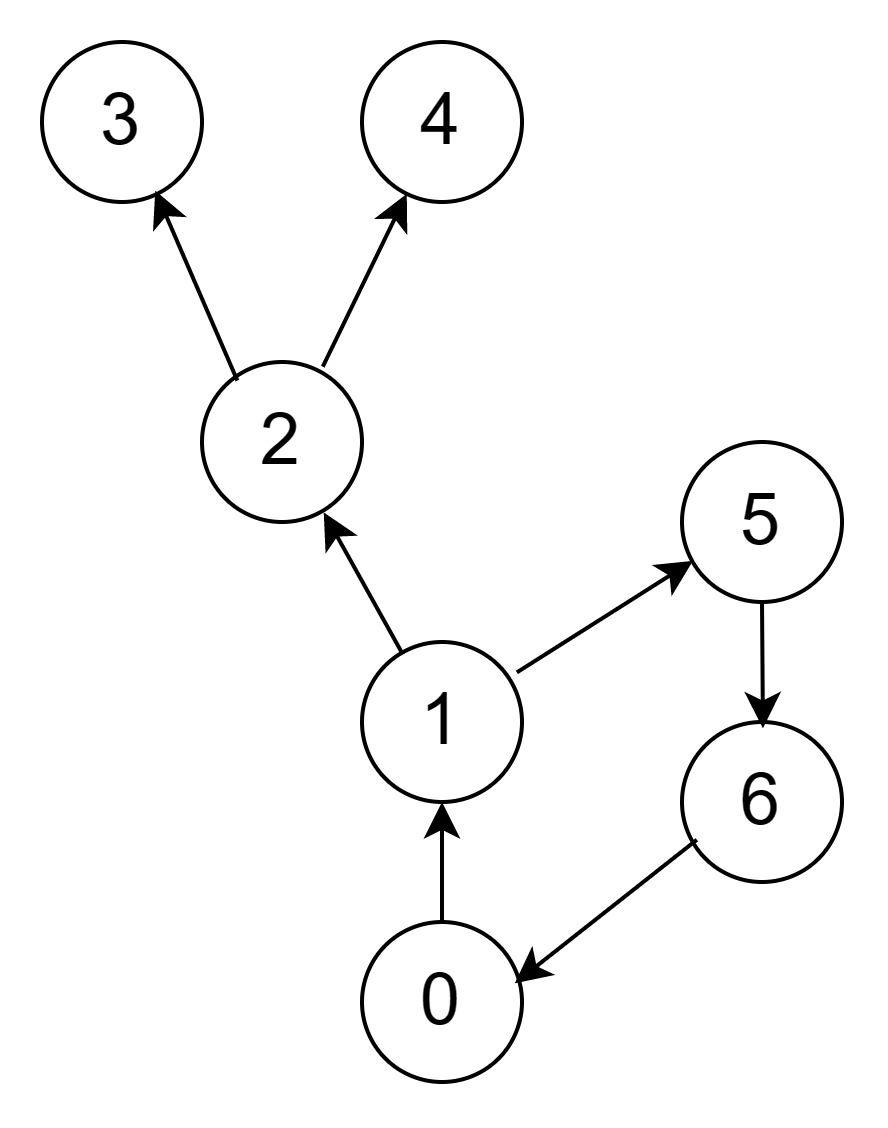
В начале все вершины в графе белые. Такому графу соответствует матрица смежности, изображенная ниже:
Начинать можно с любой вершины. Мы начнем с вершины , которой соответствует верхняя строка в матрице.
Перекрашиваем вершину в серый цвет. Это означает, что мы начали с ней работать:
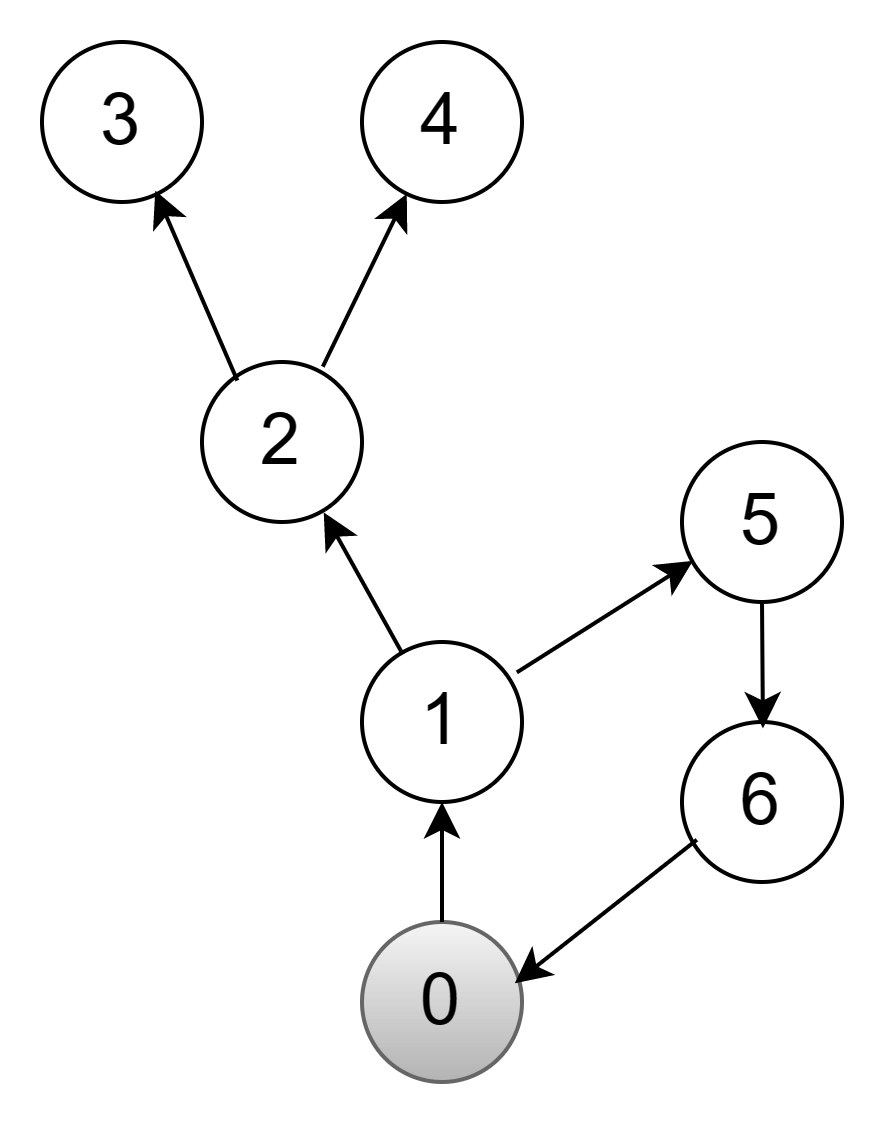
Ищем в первой строке связанные вершины. Они помечены значением .
Видим, что вершина связана со вторым элементом строки — вершиной . Начинаем работать с ней и также перекрашиваем ее в серый цвет:
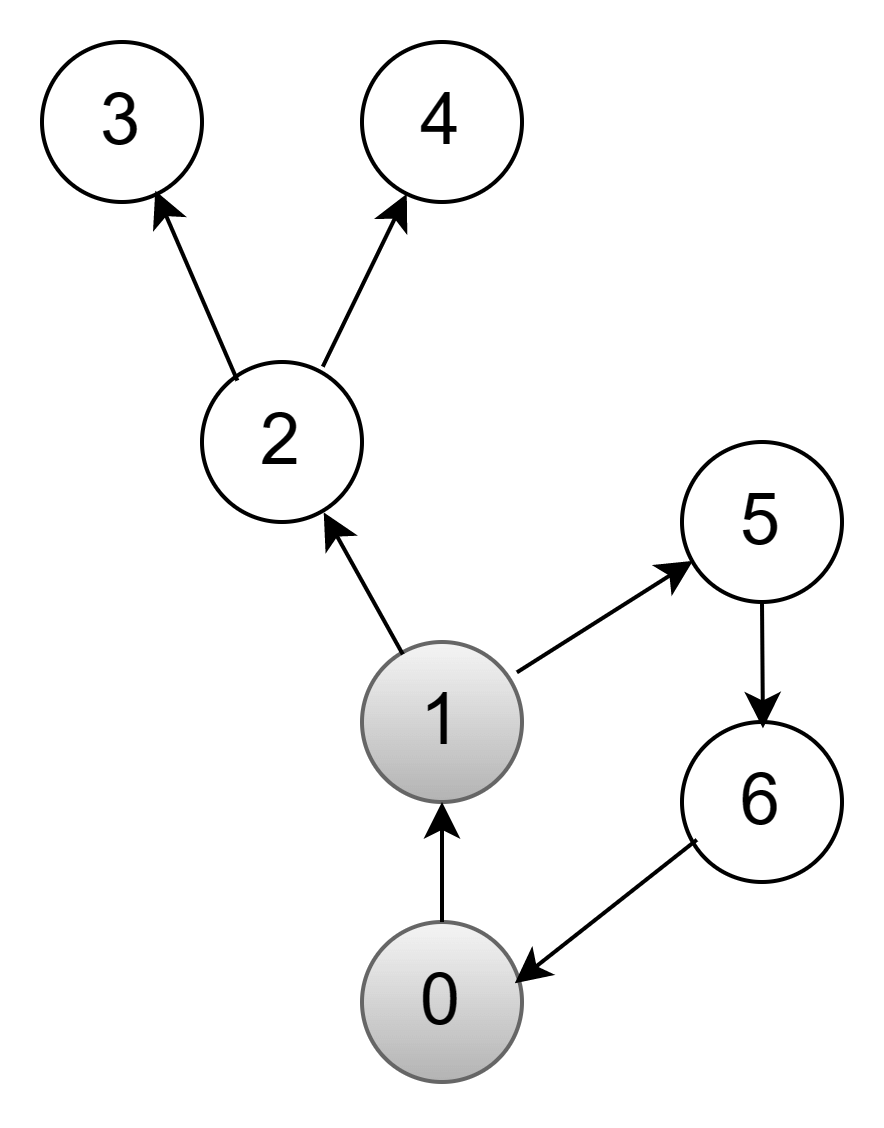
Чтобы обнаружить связанные вершины, рассмотрим вторую строку сверху. Она соответствует вершине . Похожим образом продолжаем перекрашивать вершины. Следующие на очереди — и :
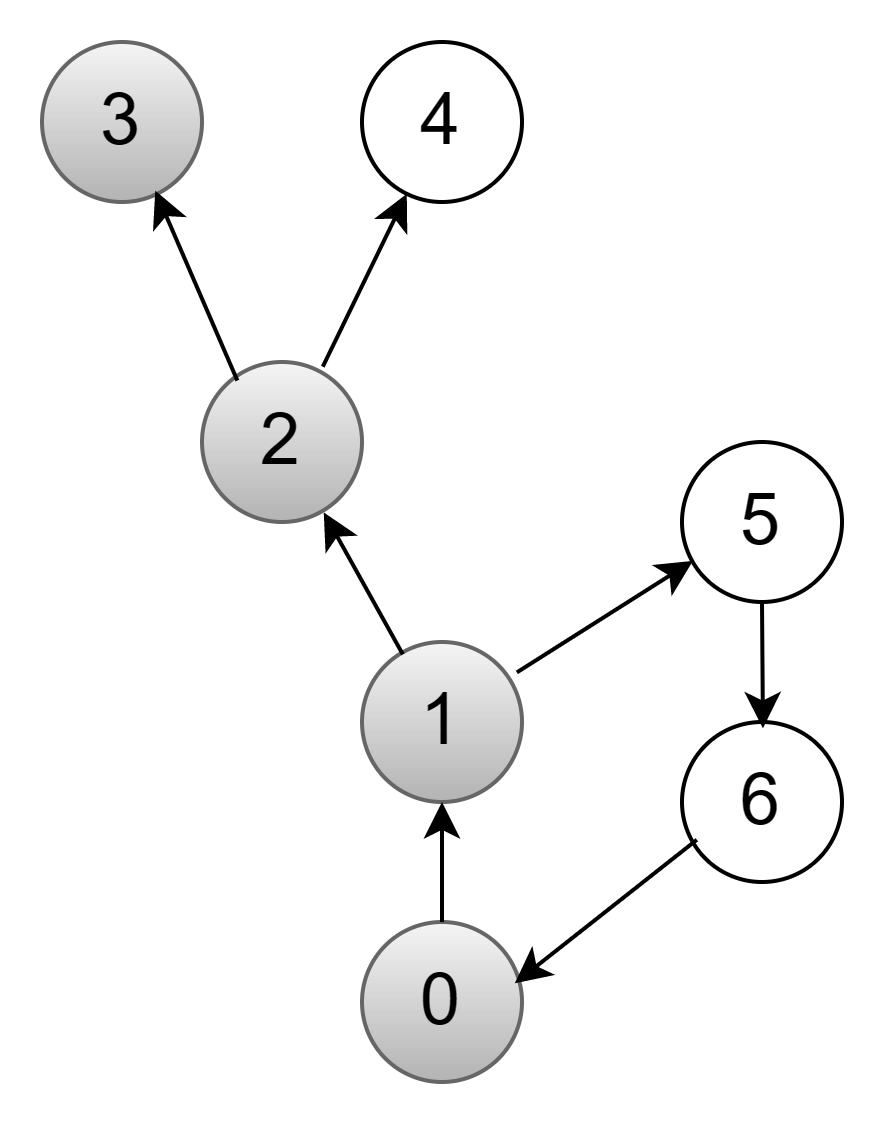
Из вершины двигаться некуда. Мы завершаем ее обработку, перекрашиваем в черный цвет и возвращаемся в вершину .
У второй вершины есть еще одна необработанная вершина — . Перекрашиваем ее в серый цвет:
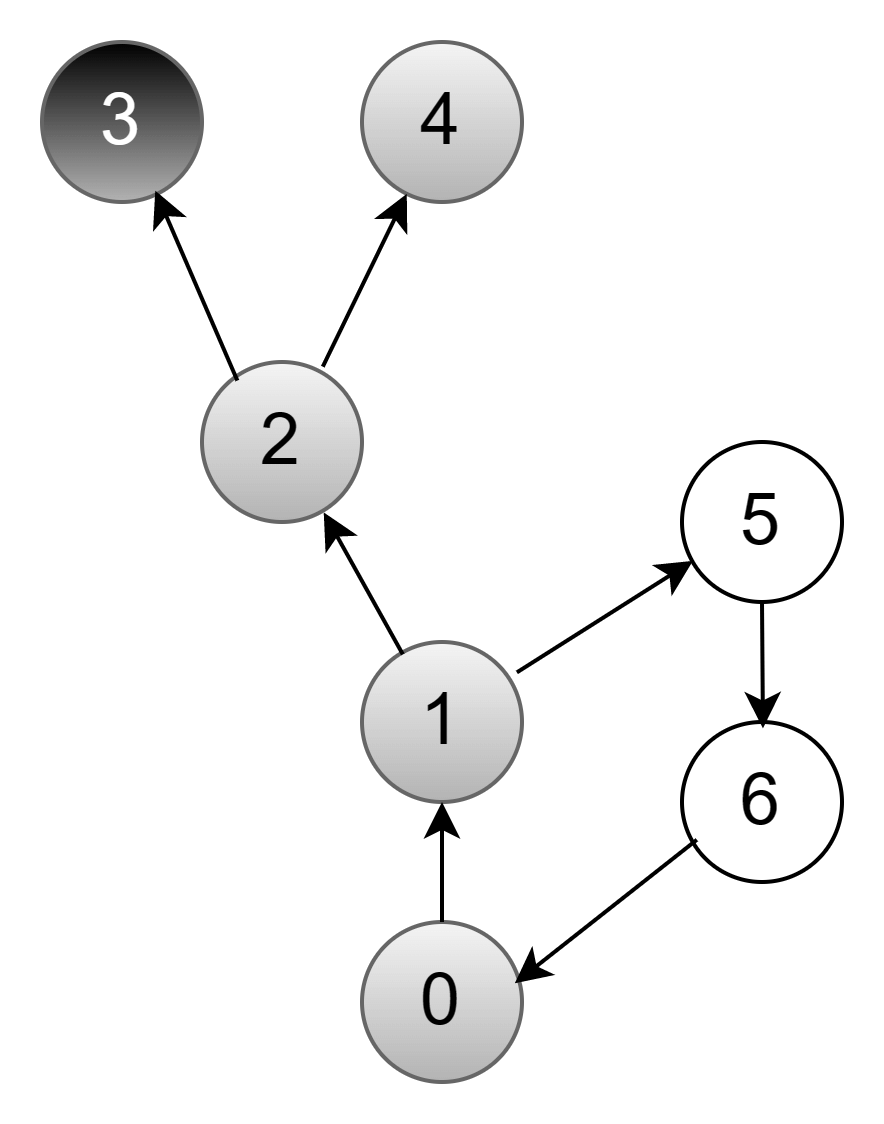
У вершины также нет связанный вершин. Завершаем ее обработку, перекрашиваем в черный цвет, снова возвращаемся в вершину 2.
Теперь и у вершины обработаны все соседи — значит, ее обработка также завершена. Перекрашиваем ее в черный цвет и возвращаемся в вершину :
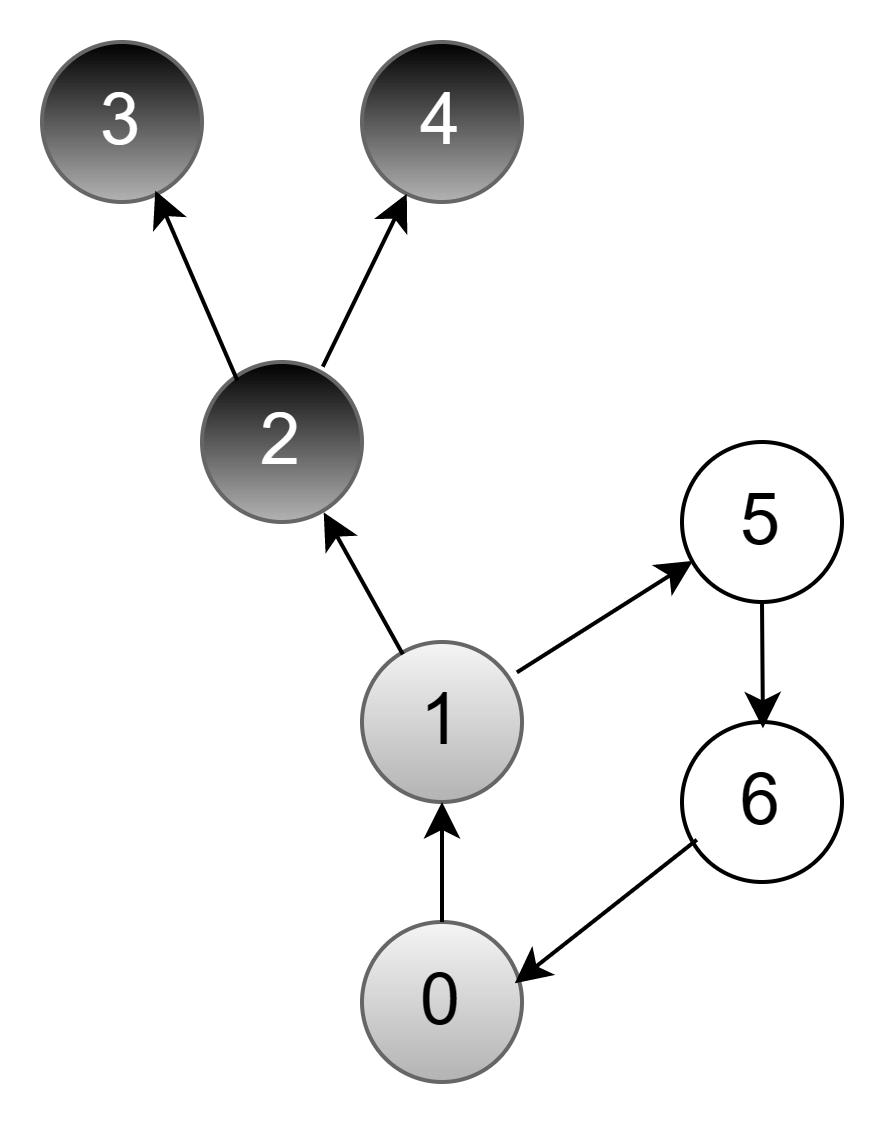
У вершины есть следующая необработанная вершина — это .
В свою очередь у вершины есть необработанная вершина :
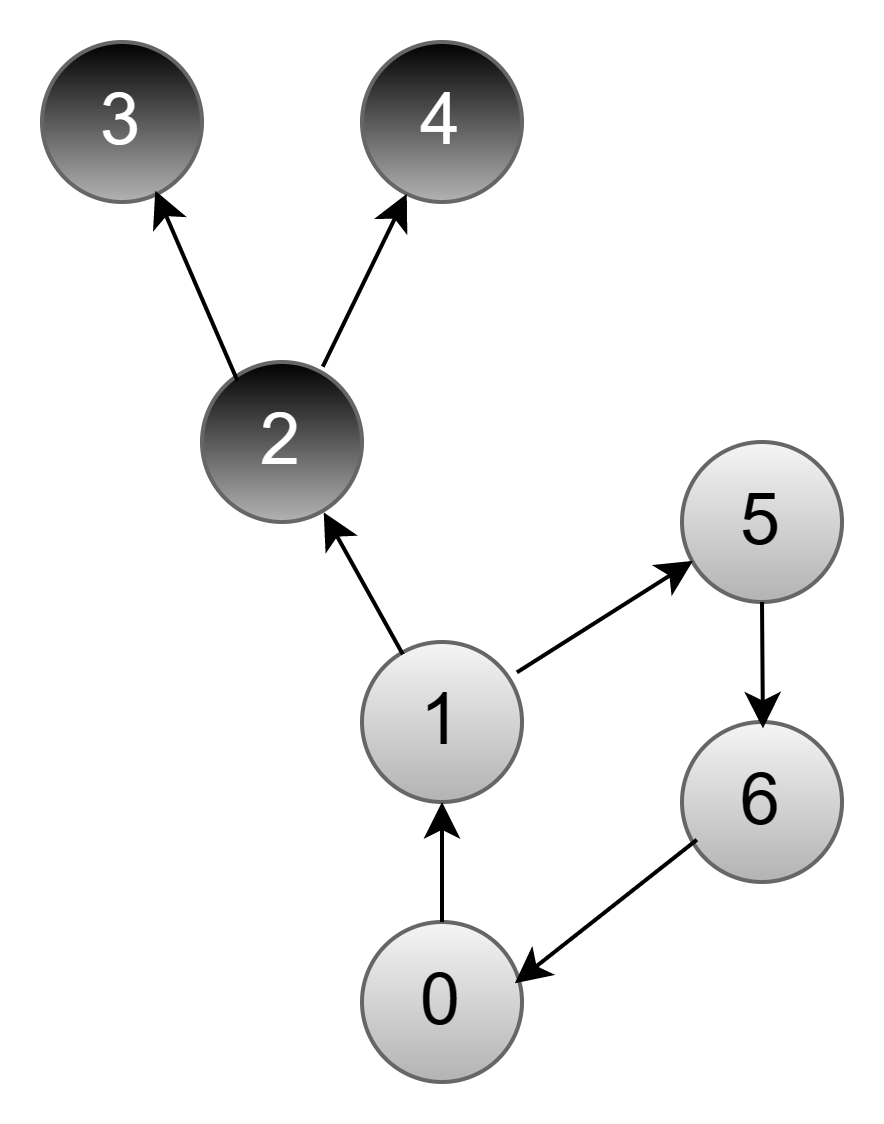
Вершина связана с вершиной , которая окрашена в серый цвет. Это значит, что мы обнаружили цикл.
Далее нужно разобраться, какие вершины входят в цикл. Для этого мы возвращаемся назад, пока не встретим вершину . Так мы выясним, что в нашем примере в цикл попадают вершины , , и .
Если мы встречаем черную вершину, это означает, что цикл в нашем графе есть, но он не опасен. Двигаясь по стрелкам, мы не попадаем в замкнутый круг:
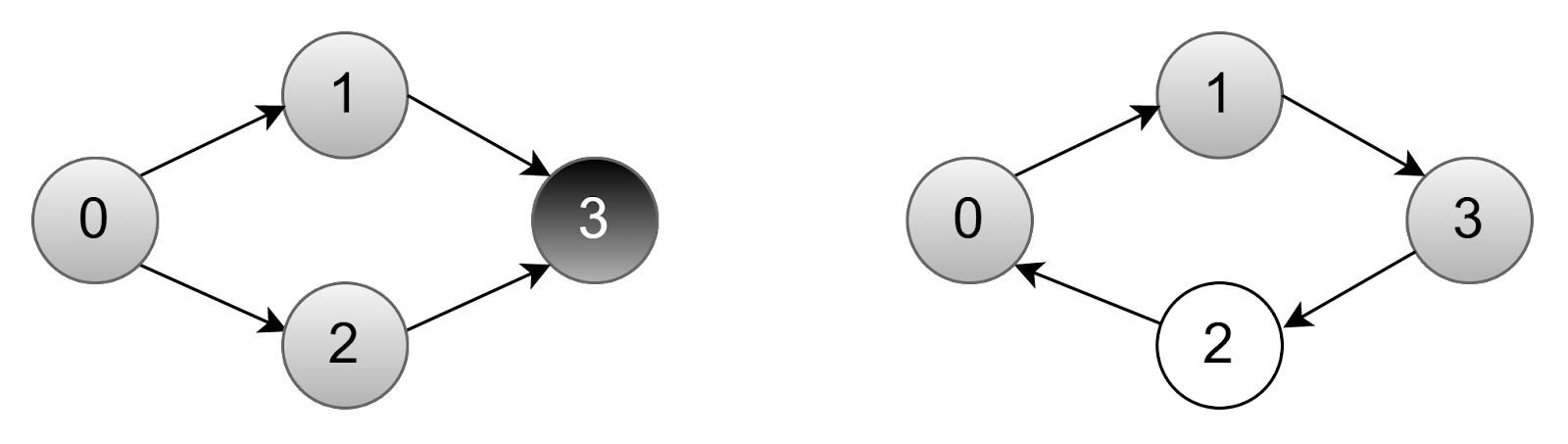
Двигаясь по стрелкам, ромб слева можно обойти без зацикливания, а ромб справа — нет. Другими словами, встречая черную вершину, мы должны ее пропускать. Черная вершина означает, что мы встретили уже обработанную область графа без циклов.
Реализация
Теперь посмотрим, как такой алгоритм реализуется в коде:
class Graph {
vertices;
size;
edges;
constructor(vertices) {
this.vertices = vertices;
this.size = vertices.length;
this.edges = Array.from({ length: this.size }, () => Array(this.size).fill(false));
}
addEdge(value1, value2) {
const row = this.vertices.indexOf(value1);
const column = this.vertices.indexOf(value2);
this.edges[row][column] = true;
}
findCycle() {
const WHITE = 0;
const GRAY = 1;
const BLACK = 2;
const colors = Array(this.size).fill(WHITE);
const visit = (i) => {
if (colors[i] === BLACK) {
return null;
} if (colors[i] === GRAY) {
return [];
}
colors[i] = GRAY;
for (let j = 0; j < this.size; j += 1) {
if (this.edges[i][j]) {
const result = visit(j);
if (Array.isArray(result)) {
return [...result, this.vertices[i]];
}
}
}
colors[i] = BLACK;
return null;
};
return visit(0);
}
}Как и в прошлых уроках, для работы с графом сделаем класс Graph. В конструкторе мы будем получать массив значений в вершинах графа. Размер массива сохраним в поле size для последующего использования. Также сразу создадим квадратную матрицу смежности, заполним ее значением false:
constructor(vertices) {
this.vertices = vertices;
this.size = vertices.length;
this.edges = Array.from({ length: this.size }, () => Array(this.size).fill(false));
}Далее мы создаем связь. По сути, это нахождение элемента в матрице и присвоение ему значения true:
addEdge(value1, value2) {
const row = this.vertices.indexOf(value1);
const column = this.vertices.indexOf(value2);
this.edges[row][column] = true;
}Для поиска циклов нам потребуются константы, чтобы обозначать белый, серый и черный цвет вершин, а также массив цветов всех вершин. В начале работы алгоритма все вершины белые:
const WHITE = 0;
const GRAY = 1;
const BLACK = 2;
const colors = Array(this.size).fill(WHITE);Функция возвращает массив вершин, образующих либо цикл, либо значение null при отсутствии циклов.
Основная работа делается во внутренней рекурсивной функции visit(). В качестве параметра она получает порядковый номер вершины. Так как нумерация начинается с нуля, первой вершине соответствует номер 0.
В массиве colors функция выясняет цвет вершины. Если вершина черная, функция сразу прекращает свою работу. Если вершина серая, функция также прекращает работу, но в качестве результата возвращает пустой массив:
if (colors[i] === BLACK) {
return null;
} if (colors[i] === GRAY) {
return [];
}В середине мы обрабатываем текущую вершину. Перекрашиваем ее в серый цвет, а после обработки всех связанных вершин — в черный:
colors[i] = GRAY;
for (let j = 0; j < this.size; j += 1) {
if (this.edges[i][j]) {
const result = visit(j);
if (Array.isArray(result)) {
return [...result, this.vertices[i]];
}
}
}
colors[i] = BLACK;
return null;Обработка связанных вершин заключается в поочередном рекурсивном вызове функции visit(). Если во время очередного вызова функция возвращает массив, это значит, что мы нашли цикл. Добавляем в массив текущую вершину и возвращаем новое значение.
Когда рекурсия развернется, в массиве окажутся все вершины из цикла. Именно этот массив и получит программист, вызвавший функцию.
Чтобы проверить наш код, создадим граф из примера выше и попытаемся найти в нем цикл:
const graph = new Graph(['0', '1', '2', '3', '4', '5', '6']);
graph.addEdge('0', '1');
graph.addEdge('1', '2');
graph.addEdge('1', '5');
graph.addEdge('2', '3');
graph.addEdge('2', '4');
graph.addEdge('5', '6');
graph.addEdge('6', '0');
const cycle = graph.findCycle(); // [ '6', '5', '1', '0' ];https://replit.com/@hexlet/algorithms-graphs-cycle-search
Выводы
В этом уроке мы обсудили поиск циклов и пришли к выводу, что этот алгоритм нам уже знаком. На самом деле, это адаптированный обход графа в глубину (Depth-first search).
Кроме того, в этом уроке вы узнали, что для хранения ориентированных графов можно использовать матрицу смежности. Так же можно хранить неориентированные графы, связывая каждую пару вершин в прямом и обратном направлении. Чтобы хранить взвешенные графы, в матрице смежности вместо булевых значений можно использовать числа.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
- Статья «Как учиться и справляться с негативными мыслями»
- Статья «Ловушки обучения»
- Статья «Сложные простые задачи по программированию»
- Вебинар «Как самостоятельно учиться»
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
