В программировании встречаются задачи, которые на первый взгляд не имеют отношения к графам, но решаются именно с помощью алгоритмов на графах. Одна из таких задач возникает на швейных фабриках, где роботы вырезают детали по выкройкам из больших кусков ткани. Для экономии ткани важно оставлять как можно меньше обрезков:
Для примера посмотрим, как выглядит неэкономный раскрой ткани. Здесь остается большой обрезок ткани:
Но если переставить детали местами, можно выкроить на одну красную деталь больше — и тогда обрезка не будет:
Чтобы решить такую задачу, можно использовать неявное представление графов. Действуя методом полного перебора, можно найти все варианты размещения деталей, чтобы площадь обрезков была как можно меньше.
Рассмотрим еще один пример похожей задачи. Она встречается при программировании банкоматов или вендинговых автоматов, где требуется выдать сумму наименьшим количеством банкнот и монет.
Представим, что нам нужно выдать 11 рублей. Эффективнее всего выдать две монеты: 10 рублей и 1 рубль. Но в автомате может не оказаться десятирублевых монет. Тогда простой алгоритм не найдет альтернативный вариант — одна монета в 5 рублей и три монеты по 2 рубля. Как и в случае с раскроем, все возможные решения можно найти только методом перебора.
Перечисленные задачи не похожи друг на друга, но их принято относить к одному классу, потому что решаются они одинаково. Название всему классу дала задача о рюкзаке. Одна из ее формулировок звучит так:
Попав в пещеру к разбойникам, Али-баба решил забрать как можно больше ценностей. У него есть рюкзак, рассчитанный на 20 килограмм. Нужно выбрать самые ценные предметы так, чтобы они уместились в рюкзак
В чем сложность задачи? Отобрать самое ценное не так уж и сложно, но есть и второе ограничение — вес предмета. Без перебора мы можем выбрать самый дорогой предмет в комнате — двадцатикилограммовый сундук. Но если проверить все варианты перебором, может оказаться, что два десятикилограммовых кувшина в сумме стоят больше. Тогда нужно унести два кувшина, а не один сундук.
В целом, в задачах о рюкзаке речь идет о множестве предметов, из которых мы должны выбрать оптимальное подмножество с учетом ограничений. В задаче о раскрое мы минимизировали площадь обрезков, а при выдаче сдачи — количество монет. В задаче о рюкзаке мы максимизируем стоимость предметов. Другими словами, во всех «задачах о рюкзаке» речь идет о множестве, наборе ограничений и оптимальном подмножестве.
Метод перебора
Перебор — это простейший способ решения задач на графе. В случае задач о рюкзаке граф обычно представлен неявно.
При этом алгоритм работает рекурсивно. Это значит, что мы начинаем с пустого рюкзака и на каждом шаге рекурсии пытаемся положить в него один из оставшихся предметов. Если максимальный вес не превышен, то мы помещаем предмет в рюкзак и опускаемся на следующий уровень рекурсии.
Рекурсия завершается, когда вес рюкзака превышен. В этот момент мы фиксируем текущее состояние рюкзака — одно из возможных решений. При этом нам не надо хранить все найденные решения, достаточно хранить самое дорогое.
Второй повод для завершения рекурсии — закончились предметы, то есть в рюкзак поместились все предметы. К сожалению, в реальной жизни так почти не бывает.
Взглянем на реализацию такого алгоритма:
const backpack = (worths, maxWeight) => {
const seen = new Set();
const result = { names: [], sumPrice: 0.0, sumWeight: 0 };
const bruteforce = (sumPrice, sumWeight) => {
let isLeaf = true;
for (const worth of worths) {
if (seen.has(worth)) {
continue;
}
if (worth.weight + sumWeight > maxWeight) {
continue;
}
seen.add(worth);
bruteforce(sumPrice + worth.price, sumWeight + worth.weight);
seen.delete(worth);
isLeaf = false;
}
if (isLeaf && sumPrice >= result.sumPrice) {
result.sumPrice = sumPrice;
result.sumWeight = sumWeight;
result.names = Array.from(seen.values())
.map((worth) => worth.name);
}
};
bruteforce(0.0, 0.0);
return result;
};Разберем этот код подробнее. Сначала мы видим функцию backpack(), внутри которой мы реализуем bruteforce() — рекурсивную функцию перебора.
В коде мы обращаемся к двум внешним переменным:
-
worths— массив ценностей -
seen— множество просмотренных ценностей
В качестве параметров мы передаем:
-
sumPrice— общая цена просмотренных ценностей -
subWeight(общий вес)
Можно было бы перебирать ценности в множестве seen, но это слишком накладно для каждого шага рекурсии. Поэтому мы перебираем ценности в цикле for. Если предмет уже просмотрен, мы сразу переходим к следующему предмету:
if (seen.has(worth)) {
continue;
}Если возникает перевес, мы также переходим к следующему предмету:
if (worth.weight + sumWeight > maxWeight) {
continue;
}Мы выполняем рекурсивные вызовы, пока мы не заполнили весь рюкзак и не достигли вершины-листа в нашем графе. Как и в дереве, листом в графе называется вершина, из которой больше некуда идти:
seen.add(worth);
bruteforce(sumPrice + worth.price, sumWeight + worth.weight);
seen.delete(worth);
isLeaf = false;Представим, что мы больше не можем положить в рюкзак ни одного предмета. Это значит, что мы достигли вершины-листа. Флаг isLeaf остается равным true:
if (isLeaf && sumPrice >= result.sumPrice) {
result.sumPrice = sumPrice;
result.sumWeight = sumWeight;
result.names = Array.from(seen.values())
.map((worth) => worth.name);
}Если мы достигли листа и нашли новый лучший результат, сохраняем его в полях переменной result.
Вот что у нас получается в результате:
const worths =
[
{ name: 'Корона', weight: 1.5, price: 150000 },
{ name: 'Кувшинчик', weight: 4, price: 60000 },
{ name: 'Кувшин', weight: 8, price: 80000 },
{ name: 'Шкатулка', weight: 2, price: 40000 },
{ name: 'Сундучок', weight: 8, price: 90000 },
{ name: 'Сундук', weight: 12, price: 120000 },
{ name: 'Диадема', weight: 1.2, price: 70000 },
{ name: 'Горшок с монетами', weight: 3, price: 40000 },
{ name: 'Сабля', weight: 8, price: 90000 },
{ name: 'Скипетр', weight: 6, price: 30000 },
];
const decision = backpack(worths, 20); // {
// names: [
// 'Сабля',
// 'Горшок с монетами',
// 'Диадема',
// 'Шкатулка',
// 'Кувшинчик',
// 'Корона'
// ],
// sumPrice: 450000,
// sumWeight: 19.7
// }https://replit.com/@hexlet/algorithms-graphs-backpack
Оценка сложности
Попробуем оценить алгоритмическую сложность метода перебора. Как и следует из названия, он перебирает все возможные решения, добираясь до них через все промежуточные вершины графа.
Представим, что у нас есть предметы 1, 2, 3, 4. Так будет выглядеть граф, который обходит метод перебора:
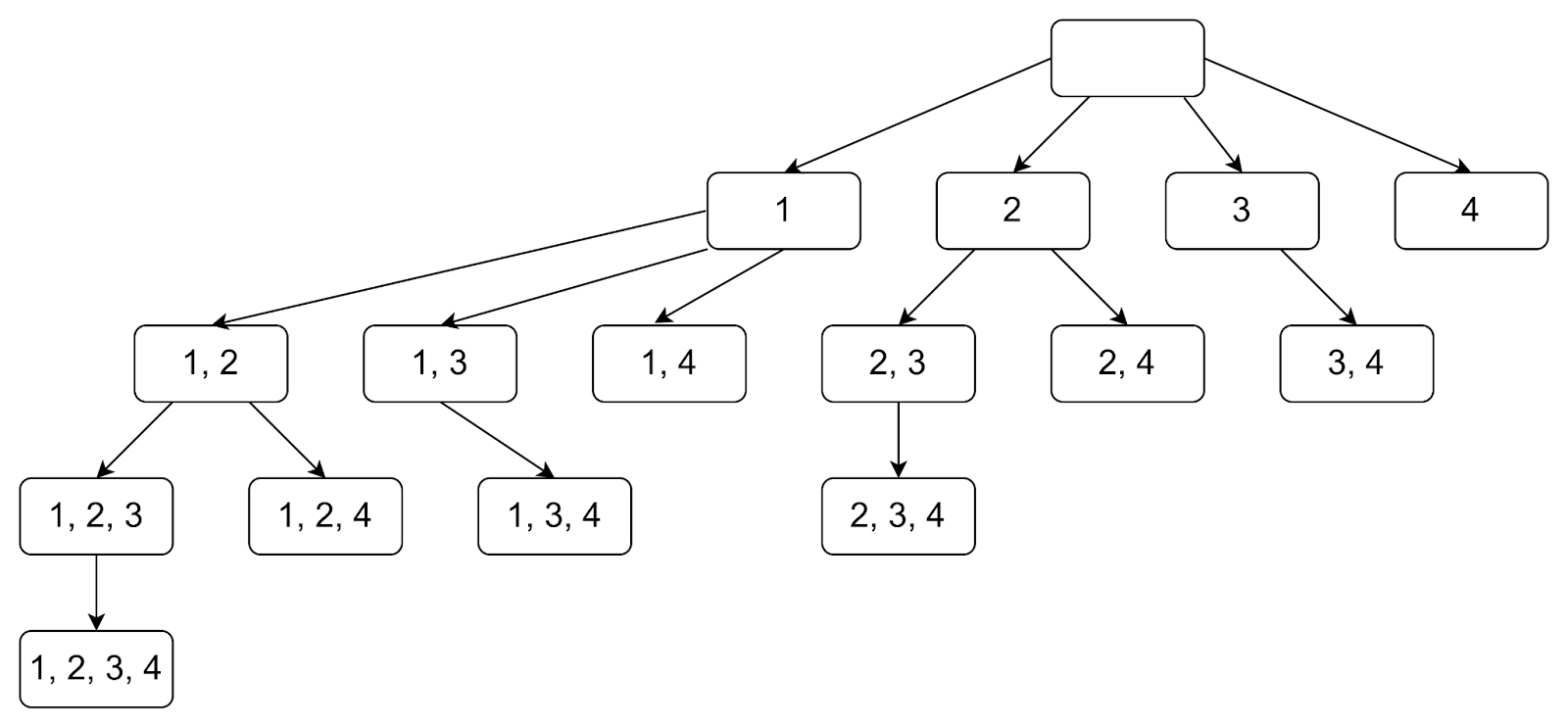
В этом графе есть 16 вершин, в том числе пустая. Рассмотрим, к какому количеству решений ведет разное количество предметов:
-
Ноль предметов дает 1 решение, то есть Али-Баба уходит с пустым рюкзаком. Так произойдет, если в пещере не найдется предмет весом менее 20 килограмм
-
Один предмет дает 2 решения — пустой рюкзак и рюкзак с этим самым предметом
-
Два предмета дают 4 решения — пустой рюкзак, рюкзак с первым предметом, рюкзак со вторым и с двумя предметами сразу. Отметим, что
-
Три предмета дают 8 решений
-
Четыре предмета дают 16 решений
Как мы видим, каждый новый предмет удваивает количество вершин. Поэтому метод перебора обладает экспоненциальной сложностью .
Это довольно медленный алгоритм. Для десяти предметов он сработает почти мгновенно, а для тридцати — займет уже несколько часов. Для шестидесяти предметов задачу решить уже невозможно — не хватит мощности всех компьютеров на Земле.
Жадный алгоритм
Как отказаться от перебора предметов на каждом шаге рекурсии? Один из подходов заключается в том, чтобы всякий раз выбирать самый ценный предмет. Работающие по этому принципу алгоритмы называются жадными.
Чтобы жадный алгоритм выбирал самые ценные предметы, нужно сравнивать не абсолютную, а удельную стоимость — то есть стоимость одного килограмма. Как и метод перебора, жадный алгоритм рекурсивно двигается по неявному графу, но на каждом шаге он выбирает одну ветвь — с наибольшей удельной стоимостью.
Без предварительной сортировки поиск максимума обладает линейной сложностью. Другими словами, в худшем случае нам придется перебрать все предметы в пещере. Итого, временная сложность жадного алгоритма равна или .
К сожалению, жадный алгоритм не всегда находит оптимальное решение. Для примера представим, что нам нужно выбрать из двух вариантов:
-
2 короны, каждая весит по 1 килограмму и стоит по 80 тысяч долларов
-
1 сундук, который весит 20 килограмм и стоит 500 тысяч долларов
Удельная стоимость корон выше, но сундук выгоднее, поэтому стоит забрать именно его. Жадный алгоритм не учтет такой вариант.
Для некоторых задач жадный алгоритм дает самое быстрое и эффективное решение. Например, в большинстве стран вендинговые автоматы выдают сдачу наименьшим числом монет именно за счет жадного алгоритма.
В таких автоматах применяется сложная математика, которая выходит за пределы данного курса. Если вам интересно изучить эту тему подробнее, можете почитать статью Canonical Coin Systems for Change-Making Problems.
Выводы
В этом уроке мы познакомились с жадными алгоритмами. Повторим ключевые мысли из урока:
-
Бывают задачи, которые похожи друг на друга по сути, несмотря на внешние различия. Такие задачи относят к одному классу. Например, существует класс «задачи о рюкзаке», по которому можно посчитать сдачу в автомате минимальным количеством монет
-
Во всех «задачах о рюкзаке» речь идет о множестве, наборе ограничений и оптимальном подмножестве. Их можно решить двумя способами — с помощью перебора или жадных алгоритмов
-
При переборе алгоритм работает рекурсивно — мы начинаем с пустого рюкзака и на каждом шаге рекурсии пытаемся положить в него один из оставшихся предметов. Если максимальный вес не превышен, то мы помещаем предмет в рюкзак и опускаемся на следующий уровень рекурсии. Рекурсия завершается, когда вес рюкзака превышен или закончились предметы
-
Перебор — это медленный алгоритм. Для десяти предметов он сработает почти мгновенно, а для тридцати — займет уже несколько часов. Для шестидесяти предметов задачу решить уже невозможно — не хватит мощности всех компьютеров на Земле
-
Жадный алгоритм выбирает самые ценные предметы, сравнивая удельную стоимость — то есть стоимость одного килограмма. Как и метод перебора, жадный алгоритм рекурсивно двигается по неявному графу, но на каждом шаге он выбирает ветвь с наибольшей удельной стоимостью
-
Без предварительной сортировки жадный алгоритм обладает линейной сложностью. Для некоторых задач жадный алгоритм дает самое быстрое и эффективное решение. Например, в большинстве стран вендинговые автоматы выдают сдачу наименьшим числом монет именно за счет жадного алгоритма
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
- Статья «Как учиться и справляться с негативными мыслями»
- Статья «Ловушки обучения»
- Статья «Сложные простые задачи по программированию»
- Вебинар «Как самостоятельно учиться»
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
