Наверняка вы пользовались сайтами для поиска авиабилетов. Вы вводили дату полета и выбирали два города — вылета и прилета. Если бы речь шла только о прямых рейсах, алгоритм поиска был бы простым.
Но есть города, не связанные напрямую — добраться из одного в другой можно только с пересадкой. Простой алгоритм такие маршруты не найдет, поэтому нам нужно что-то более мощное.
В этом уроке мы познакомимся с инструментом, который помогает решать такие задачи. Мы обсудим представление графов в памяти компьютера с помощью списка смежности и поиска в глубину. Они помогут нам строить маршруты и решать другие похожие задачи.
Список смежности
Любой граф состоит из вершин и ребер. В задаче поиска авиабилетов вершины — это города. Если два города связаны авиасообщением, их соединяет ребро:
У каждой вершины есть значение — это название города. Из каждой вершины выходит несколько ребер, которые удобно хранить в массиве:
class Vertex {
constructor(value) {
this.value = value;
this.adjacentVertices = [];
}
addLink(vertex) {
if (!this.isLinked(vertex)) {
this.adjacentVertices.push(vertex);
vertex.adjacentVertices.push(this);
}
}
isLinked(vertex) {
return this.adjacentVertices.includes(vertex);
}
}Класс Vertex хранит одну вершину и массив ссылок на соседние вершины. При создании экземпляра Vertex мы сохраняем значение вершины в поле value и создаем пустой массив смежных вершин adjacentVertices.
В переводе с английского adjacent vertices — смежные вершины. Обычно множественное число образуется с помощью суффикса -s или -es. Вершина (vertex) — это то редкое слово, для которого это правило не работает. По-английски вершины — это vertices, а не vertexes.
В классе есть метод addLink(), который устанавливает связь с другой вершиной:
if (!this.isLinked(vertex)) {
this.adjacentVertices.push(vertex);
vertex.adjacentVertices.push(this);
}Программист может по ошибке вызывать метод addLink() несколько раз для одного и того же города. Чтобы не дублировать вершины в списке смежности, мы убеждаемся, что город не был добавлен ранее — в этом смысл оператора if.
Метод isLinked() проверяет, связаны вершины или нет.
Не бывает так, что самолеты летают только в одну сторону. Добавляя город Б в список смежности города А, мы должны одновременно добавить А в список смежности Б.
Именно так в списках смежности можно хранить неориентированные графы. По сути, мы храним ориентированный граф, вершины которого связаны ребрами, направленными навстречу друг другу, как это показано на рисунке:
В списке смежности мы храним вершину, а не ребро, поэтому внутри if мы добавляем вершины в списки смежности друг друга:
this.adjacentVertices.push(vertex);
vertex.adjacentVertices.push(this);Написанный нами код уже можно использовать, чтобы хранить информацию об авиасообщениями между городами:
const city1 = new Vertex('Новосибирск');
const city2 = new Vertex('Омск');
city1.addLink(city2);
console.log(city2.isLinked(city1)); // <= trueПостроение графа
Нам предстоит работать не с отдельными вершинами, а с графом. Полезно инкапсулировать в одном классе вершины и методы для работы с вершинами:
class Graph {
vertices = [];
getVertex(value) {
return this.vertices.find(x => x.value === value);
}
addVertex(value) {
if (this.getVertex(value) === undefined) {
this.vertices.push(new Vertex(value));
}
}
addEdge(value1, value2) {
const vertex1 = this.getVertex(value1);
const vertex2 = this.getVertex(value2);
if (vertex1 !== undefined && vertex2 !== undefined) {
vertex1.addLink(vertex2);
}
}
}Метод addVertex() добавляет в граф новую вершину с заданным значением (value) и пустым списком смежности. Перед добавлением метод проверяет, что в графе нет вершины с таким же значением — так мы можем отличать вершины друг от друга. Метод addEdge() добавляет ребро между вершинами.
Пользуясь методами addVertex и addEdge, мы можем построить граф:
const graph = new Graph();
graph.addVertex('Москва');
graph.addVertex('Санкт Петербург');
graph.addVertex('Калининград');
graph.addVertex('Омск');
graph.addVertex('Новосибирск');
graph.addVertex('Якутск');
graph.addEdge('Санкт Петербург', 'Калининград');
graph.addEdge('Калининград', 'Москва');
graph.addEdge('Калининград', 'Якутск');
graph.addEdge('Москва', 'Якутск');
graph.addEdge('Москва', 'Омск');
graph.addEdge('Москва', 'Новосибирск');
graph.addEdge('Омск', 'Новосибирск');
const races = graph.getVertex('Новосибирск').adjacentVertices;
console.log(races[0].value); // => 'Москва'Метод getVertex() возвращает вершину с заданным значением (value). С помощью него мы убеждаемся, что граф построен корректно.
Обход графа в глубину
В реальных системах поиска авиабилетов учитываются разные атрибуты — даты, время прилета и отлета, класс обслуживания, наличие багажа и другие.
Чтобы не усложнять учебный материал, мы решим более простую задачу — построим маршрут. Например, наша программа сможет ответить на вопрос: «Как добраться из Новосибирска в Калининград?». При этом мы будем учитывать не только прямые варианты перелета, но и маршруты с одной, двумя и даже тремя пересадками.
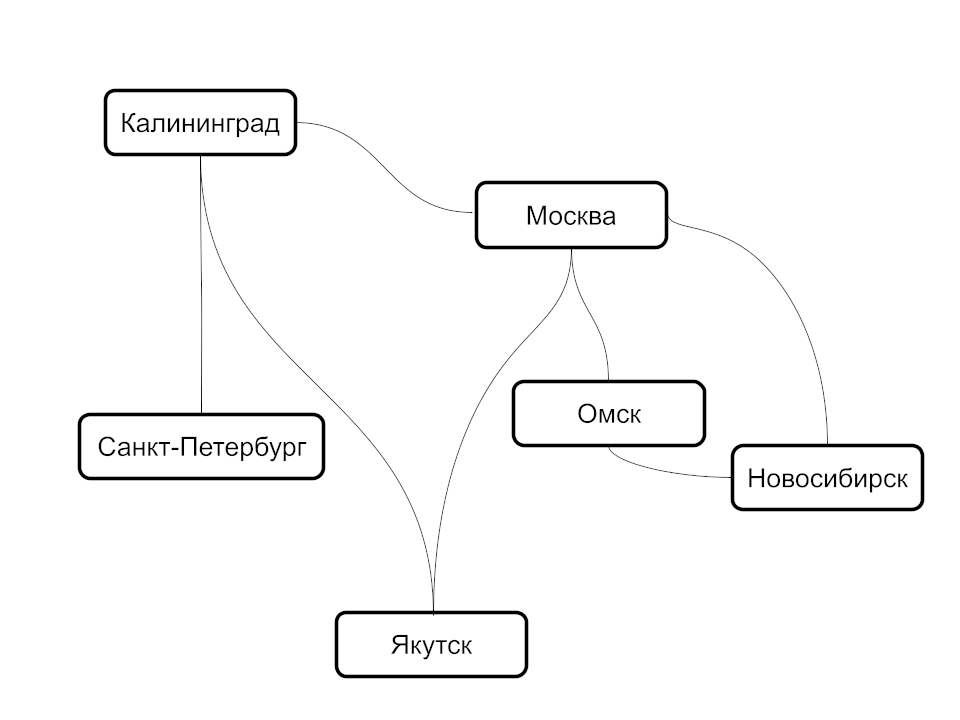
Перед реализацией порассуждаем, как должен работать наш алгоритм. Возьмем для примера перелет из Новосибирска в Калининград:
-
Начинаем обход в глубину с вершины, из которой мы строим маршрут — из Новосибирска
-
Выясняем, что из Новосибирска можно улететь в Омск и Москву
-
Выбираем первое ребро (Омск) и снова смотрим список смежных вершин
-
Выясняем, что из Омска можно улететь в Москву и Новосибирск
-
Следующей точкой выбираем Москву и смотрим список смежных вершин
-
Алгоритм повторяется до тех пор, пока мы не достигнем конечной точки — Калининграда
Просмотренные вершины и есть наш маршрут — Новосибирск, Омск, Москва, Калининград. А теперь усложним задачу и поищем все варианты маршрута:
-
Возвращаемся к предыдущему городу в списке — к Москве
-
Рассматриваем следующую вершину в списке смежности — Якутск
-
Продолжая обход, мы обнаружим новый маршрут — Новосибирск, Омск, Москва, Якутск, Калининград
-
Заканчивая обход списков смежности, мы постоянно возвращаемся к предыдущей вершине. Другими словами, перебрав все рейсы из Москвы, мы откатываемся к Омску, а затем — к Новосибирску
Можно заметить, что простая реализация поиска войдет в бесконечный цикл. Города связаны взаимным авиасообщением. Если мы можем улететь из Новосибирска в Омск, значит, мы можем улететь и обратно. Омск и Новосибирск находятся в списках смежности друг у друга.
Перебирая вершины без дополнительных проверок, мы обнаружим бесконечный цикл: Новосибирск, Омск, Новосибирск, Омск, Новосибирск, Омск…
Чтобы алгоритм не зациклился, нужно по мере обхода графа сохранять вершины, которые мы посетили и отбрасывать их при переборе.
Действия на каждом шаге алгоритма повторяются, поэтому код можно оформить в виде рекурсивной функции:
#recursiveDepthFirstSearch(current, end, visited, routes) {
visited.push(current);
if (current === end) {
const route = visited.join('-');
routes.push(route);
} else {
const neighbours = this.getVertex(current).adjacentVertices;
for (let i = 0; i < neighbours.length; i += 1) {
const next = neighbours[i].value;
if (!visited.includes(next)) {
this.#recursiveDepthFirstSearch(next, end, visited, routes);
}
}
}
visited.pop(current);
}Здесь мы видим рекурсивный метод #recursiveDepthFirstSearch. В его названии есть #, которая обозначает, что он приватный — может быть вызван только из других методов класса Graph.
Метод принимает четыре параметра:
-
current -
end -
visited -
routes
Начнем с первых двух. Параметр current содержит значение текущей вершины, а end — значение конечной вершины. Если текущая вершина совпадает с конечной, мы нашли очередной маршрут:
const route = visited.join('-');
routes.push(route);Сливаем названия городов, разделив их дефисом. Маршрут будет представлять собой строку вида 'Новосибирск-Москва-Калининград'.
Еще есть переменные visited и routes — это третий и четвертый параметры метода. В visited складываются все посещенные вершины — в нашем случае это названия городов. Объединив эти названия, мы получаем маршрут.
Массив visited тоже заполняется внутри метода. В первой строке мы помещаем в него текущую вершину current, а в последней — удаляем ее. Вершину надо удалять, когда мы откатываемся назад по маршруту, потому что в другой ветке мы снова можем попасть в тот же город, но уже другим путем.
Параметр routes не только входной, но и выходной. Это массив, в который складываются найденные маршруты. Когда метод #recursiveDepthFirstSearch обойдет весь граф, в массиве окажутся все способы добраться из начальной точки в конечную.
Внутри цикла мы перебираем все соседние вершины. Если какая-то из них есть в массиве visited, мы ее пропускаем. В противном случае мы делаем вершину текущей и рекурсивно вызываем метод #recursiveDepthFirstSearch:
const neighbours = this.getVertex(current).adjacentVertices;
for (let i = 0; i < neighbours.length; i += 1) {
const next = neighbours[i].value;
if (!visited.includes(next)) {
this.#recursiveDepthFirstSearch(next, end, visited, routes);
}
}Мы сделали метод приватным, потому что у него есть служебные параметры visited и routes. Для программистов, которые будут пользоваться поиском, сделаем простой метод без лишних параметров:
dfs(start, end) {
const visited = [];
const routes = [];
this.#recursiveDepthFirstSearch(start, end, visited, routes);
return routes;
}Выше мы использовали метод dfs() — это deep first search или «поиск в глубину». Вызвав метод dfs() для графа, который мы построили в предыдущем разделе, получим список возможных маршрутов:
console.log(graph.dfs('Новосибирск', 'Калининград'));
// => [
// 'Новосибирск-Москва-Калининград',
// 'Новосибирск-Москва-Якутск-Калининград',
// 'Новосибирск-Омск-Москва-Калининград',
// 'Новосибирск-Омск-Москва-Якутск-Калининград'
// ]https://replit.com/@hexlet/algorithms-graphs-dfs-graph
Итеративная реализация
Любой рекурсивный алгоритм можно преобразовать в итеративный. В некоторых случаях реализация оказывается простой, но при обходе графа нам придется складывать вершины в стек.
В JavaScript в качестве стека можно использовать обычный массив, у которого есть методы push() и pop():
iterativeDfs(startValue, endValue) {
const start = this.getVertex(startValue);
const routes = [];
const vertices = [{ current: start, visited: [] }];
while (vertices.length > 0) {
const top = vertices.pop();
const { current } = top;
const visited = [...top.visited, current.value];
if (current.value === endValue) {
const route = visited.join('-');
routes.push(route);
} else {
for (let i = 0; i < current.adjacentVertices.length; i += 1) {
const next = current.adjacentVertices[i];
if (!visited.includes(next.value)) {
vertices.push({ current: next, visited });
}
}
}
}
return routes;
}https://replit.com/@hexlet/algorithms-graphs-dfs-graph
В массив (стек) vertices мы складываем вершины для обхода. Перед циклом while мы помещаем туда начальную вершину, из которой строим маршрут.
В цикле снимаем с вершины стека очередную вершину и проверяем, не является ли она конечной. Достигнув конечного города, добавляем в массив routes очередной обнаруженный маршрут и переходим к следующей вершине на стеке.
Если очередная вершина промежуточная, убеждаемся, что она не встречается в массиве посещенных вершин visited. В стеке могут одновременно находиться десятки вершин — строящиеся маршруты. У каждой из них свой набор посещенных вершин. Чтобы они не путались, мы храним массив visited вместе с вершиной в стеке.
В целом, реализация получается не намного сложнее рекурсивной версии.
Выводы
Повторим ключевые мысли этого урока:
-
Для представления графов в памяти компьютеров используют списки смежности
-
Граф хранится как список вершин (массив)
-
Вершины содержат значение и массив — список смежности, в котором перечислены ссылки на связанные вершины
-
Для представления неориентированного графа вершины заносятся в списки смежности друг друга. Это ориентированный граф, у которого каждая пара вершин связана парой встречных ребер
-
Поиск в глубину (Deep First Search, DFS) — алгоритм обхода графа, который движется от начальной вершины как можно дальше сначала по первому ребру, потом по второму, и так далее
-
Поиск в глубину можно использовать для перебора вершин, чтобы найти вершину с заданным значением. Также можно построить маршрут от вершины до вершины, или построить все возможные маршруты
-
Простейшая реализация поиска в глубину — рекурсивная. Мы можем сделать ее итеративной, но тогда придется явно использовать стек
-
Если в графе есть циклы, нам во время обхода нужно хранить список посещенных вершин
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
