- Решаем задачу «в лоб»
- Реализуем первый алгоритм
- Ускоряем алгоритм
- Изучаем алгоритм Левенштейна
- Реализуем алгоритм Левенштейна
- Выводы
Люди часто ошибаются при вводе текста. Именно поэтому компьютеры научились понимать слова с опечатками:
Google понимает, что вместо слова ТОКОЕ имеется в виду слово ТАКОЕ. Но как он это делает? Вряд ли можно составить словарь всех опечаток. Один из способов найти подходящее слово заключается в расчете редакционного расстояния.
Редакционное расстояние — это минимальное количество букв, которые нужно вставить, удалить или заменить, чтобы получить из одного слова другое.
Рассмотрим пару примеров. Чтобы превратить:
-
СТОЛ в СТОП, надо заменить букву Л на П
-
СТОЛ в СТОЛЫ — добавить букву Ы
-
СТОЛ в СТО — удалить букву Л
В каждом из этих случаев редакционное расстояние равно единице.
Чтобы превратить СТОЛ в ТОНА, потребуется три преобразования:
-
СТОЛ → ТОЛ
-
ТОЛ → ТОН
-
ТОН → ТОНА
Следовательно, редакционное расстояние между словами СТОЛ и ТОНА равно трем.
Если мы не обнаружили слово в словаре, мы можем поискать слова, которые находятся от него на небольшом редакционном расстоянии. Слова ТОКОЕ в словаре нет, но есть слово ТАКОЕ. Редакционное расстояние между словами равно единице, поэтому ТАКОЕ — хороший кандидат на замену.
Но как вычислять редакционное расстояние?
Решаем задачу «в лоб»
В решении этой задачи нам помогут графы. Для начала попробуем сформулировать алгоритм расчета редакционного расстояния, но это не так просто сделать.
Когда мы сталкиваемся с опечаткой, мы определяем, что именно пошло не так:
-
Вместо правильной буквы стоит неправильная
-
Нужная буква пропущена
-
В слове появилась лишняя буква
Представим, что мы встретили слово ТОКОЕ и поняли, что здесь есть опечатка — нужно поставить А вместо О. Алгоритм мог бы по буквам сравнить слова ТОКОЕ и ТАКОЕ и обнаружить расхождение во второй букве. Но вдруг речь идет не о замене, а о лишней букве? Чтобы принять решение, надо заглянуть на одну букву вперед. Если речь идет о двух или трех буквах, заглядывать придется еще дальше.
Кажется, такой код будет состоять из бесчисленных операторов if, вложенных друг в друга. Это не самый простой способ.
Решение через графы заключается в том, что мы допускаем все возможные варианты и выбираем среди них вариант с наименьшим расстоянием. Предположим, мы хотим узнать редакционное расстояние для пары слов ВХОД → ВДОХ.
Первая буква — В — совпадает в обоих случаях. При этом мы не можем исключить и вариантов с лишней или пропущенной буквой. Чтобы убедиться в этом, изучим такие примеры
-
Пара ВВЕСТИ → ВЕСТИ. Чтобы превратить первое слово во второе, нужно убрать первую букву В — то есть она лишняя
-
Пара ВЕСТИ → ВВЕСТИ. Чтобы превратить первое слово во второе, придется вставить букву В — она недостающая
Обратите внимание на интересную симметрию. Вставка буквы в начало первого слова — по сути то же самое, что и удаление первой буквы из второго слова.
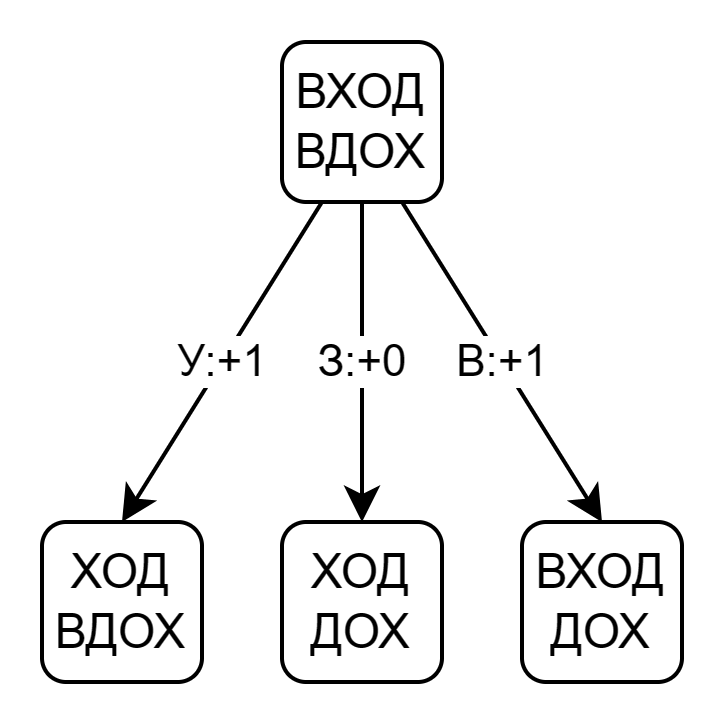
Начинаем сравнивать слова слева направо. На рисунке показана вершина графа решения:
Рассмотрим граф подробнее:
-
Левый дочерний узел соответствует удалению (У). Удаление увеличивает редакционное расстояние на единицу. Если мы уберем первую букву слово ВХОД превратится в ХОД, а слово ВДОХ не изменится
-
Средний узел — это замена (З). Нам не нужно менять В на В, поэтому редакционное расстояние не увеличивается. После сравнения отбрасываем первые буквы в обоих словах, так что у нас остаются ХОД и ДОХ
-
Правый дочерний узел — это вставка (В). Вставка буквы в первое слово — то же самое, что удаление буквы из второго слова. В итоге получаем пару ВХОД и ДОХ, при этом редакционное расстояние увеличивается на единицу
В общем, мы не просто вычисляем редакционного расстояния между словами ВХОД и ВДОХ. Мы сводим этот процесс к вычислению расстояний для трех более коротких слов:
-
ХОД и ВДОХ
-
ХОД и ДОХ
-
ВХОД и ДОХ
Выше мы свели эту сложную задачу к простой — значит, в этом случае будет удобно использовать рекурсию.
В курсе по алгоритмам мы знакомились с рекурсивными алгоритмами. Рекурсия завершится, когда в обоих словах не останется букв. Тогда эти пустые слова совпадут друг с другом, поэтому редакционное расстояние между ними будет равняться нулю.
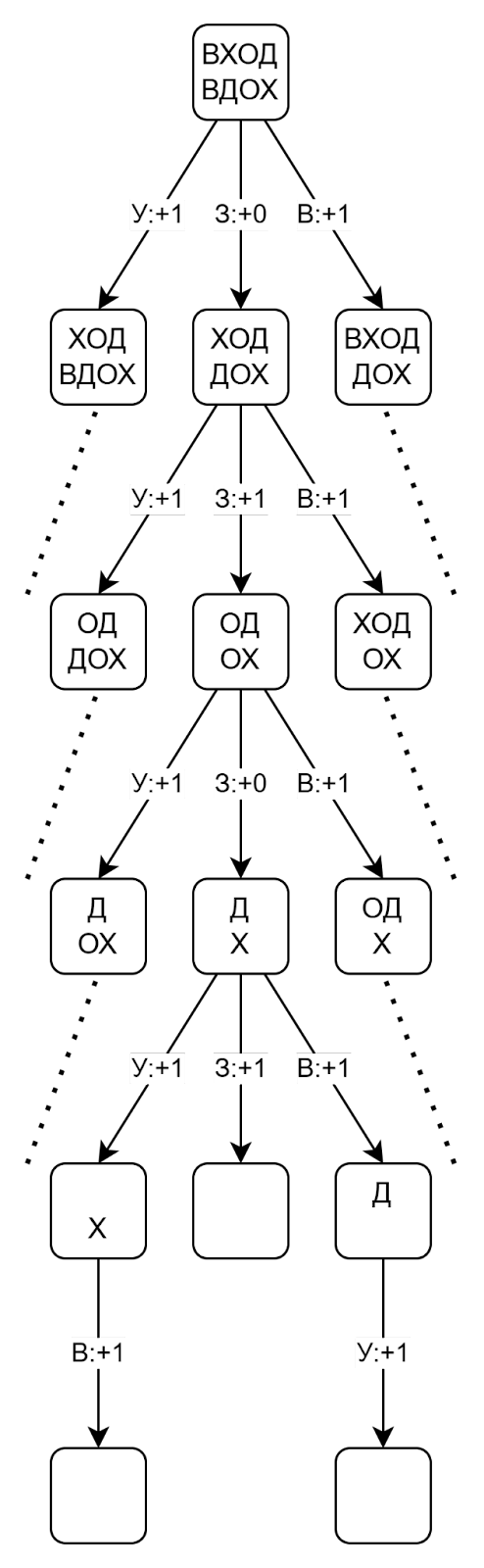
На рисунке показана часть графа, которая соответствует решению задачи:
Если буквы остались только в первом слове, то мы сравниваем это слово с пустой строкой. Нам доступны только операции удаления:
-
ХОД → ОД
-
ОД → Д
-
Д → пустая строка
Аналогично, если буквы остались только во втором слове, нам доступны только операции вставки:
-
Пустая строка → Д
-
Д → ОД
-
ОД → ХОД
Замена возможна, только если буквы для сравнения остались в обоих словах.
Граф решения может включать самые экзотические варианты преобразований. Например:
-
ВХОД → ХОД (удаление)
-
ХОД → ОД (удаление)
-
ОД → Д (удаление)
-
Д → Х (замена)
-
Х → ОХ (вставка)
-
ОХ → ДОХ (вставка)
-
ДОХ → ВДОХ (вставка)
Это тоже решение задачи. Но редакционное расстояние определяется как минимальное количество операций. Поэтому на каждом шаге мы вычисляем три дочерних расстояния и мы выбираем наименьшее из них.
Наименьшее редакционное расстояние между словами ВХОД → ВДОХ равно двум. Оно соответствует двум заменам:
-
ВХОД → ВДОД
-
ВДОД → ВДОХ
Реализуем первый алгоритм
Реализация алгоритма не очень сложная. От описанного алгоритма она отличается небольшой оптимизацией.
Дело в том, что удаление буквы из начала слова — ресурсоемкая операция. Вместо удаления мы заводим переменные index1 и index2, которые указывают на очередную букву в первом и во втором слове. Другими словами, они хранят порядковый номер буквы, начиная с нуля.
Вместо реального удаления буквы мы просто увеличиваем index1 или index2 на единицу:
const distance = (word1, word2) => {
const recursive = (index1, index2) => {
if (index1 === word1.length && index2 === word2.length) {
return 0;
}
const subDistances = [];
// Комментарии с вопросом — это конструкции с `if`
// Алгоритм проверяет, можно ли сделать замену, вставку или удаление
// Если можно, то код выполняется
// Замена?
if (index1 < word1.length && index2 < word2.length) {
if (word1.charAt(index1) === word2.charAt(index2)) {
subDistances.push(recursive(index1 + 1, index2 + 1));
} else {
subDistances.push(1 + recursive(index1 + 1, index2 + 1));
}
}
// Удаление?
if (index1 < word1.length) {
subDistances.push(1 + recursive(index1 + 1, index2));
}
// Вставка?
if (index2 < word2.length) {
subDistances.push(1 + recursive(index1, index2 + 1));
}
return Math.min(...subDistances);
};
return recursive(0, 0);
};https://replit.com/@hexlet/algorithms-graphs-levenshtein-distance
Внутри функции distance() мы создаем рекурсивную функцию recursive(). В самом начале этой функции мы проверяем, есть ли у нас буквы для сравнения хотя бы в одном слове.
Если букв нет, мы дошли до конечного узла, в нем сравниваются два пустых слова. Значит, результат равен нулю:
if (index1 == word1.length && index2 == word2.length) {
return 0;
}Иногда у нас будет три дочерних расстояния, а иногда — только одно. Чтобы обрабатывать эти варианты универсальным способом, создадим массив дочерних расстояний:
let subDistances = [];
// Замена?
if (index1 < word1.length && index2 < word2.length) {
if (word1.charAt(index1) == word2.charAt(index2)) {
subDistances.push(recursive(index1 + 1, index2 + 1));
} else {
subDistances.push(1 + recursive(index1 + 1, index2 + 1));
}
}Если буквы в словах совпадают, замена не нужна — ее стоимость равна нулю. Если буквы различаются, добавляем единицу. В случае замены мы избавляемся от обеих букв в начале слова. Поэтому при рекурсивном вызове увеличиваем на единицу обе переменные — index1 и index2:
// Удаление?
if (index1 < word1.length) {
subDistances.push(1 + recursive(index1 + 1, index2));
}
// Вставка?
if (index2 < word2.length) {
subDistances.push(1 + recursive(index1, index2 + 1));
}Удаление и вставка очень похожи друг на друга. Вставка буквы в первое слово — то же самое, что и удаление буквы из второго слова:
return Math.min(...subDistances);Завершаем рекурсивную функцию возвратом минимального расстояния.
Функция distance() вызывает ее с параметрами 0 и 0, которые соответствуют первым буквам:
return recursive(0, 0);Проверим работу функции:
distance('вход', 'вдох'); // 2
distance('ввход', 'выдох'); // 3
distance('муха', 'слон'); // 4Алгоритм кажется хорошим, пока мы не оценили его сложность. На каждом шаге мы строим три дочерних узла, перемещаясь при этом на одну букву. Количество узлов в таком графе равно , где и — длины первого и второго слова. Это верхняя граница. Реальное количество узлов будет меньше, но экспоненциальный рост количества узлов налицо.
Для вычисления редакционного расстояния между словами ВХОД и ВДОХ придется построить 520 узлов, что довольно много. Нет ли способа ускорить этот алгоритм?
Ускоряем алгоритм
Посмотрим на граф решения и обнаружим одни и те же узлы в разных его местах:
На рисунке цветом выделены повторяющиеся подграфы. Редакционные расстояния в этих подграфах совпадают, поэтому мы можем вычислить их только один раз и сохранить на будущее.
Этот подход похож на кеширование. При кэшировании программа запоминает результат чтения с диска, скачивания по сети или других длительных операций.
Здесь мы запоминаем результат длительных вычислений. Кеширование вычислений программисты называют мемоизацией. Этот термин произошел от слова memory, которое переводится как «память».
Посмотрим, как это выглядит в коде:
const fastDistance = (word1, word2) => {
const map = new Map();
const recursive = (index1, index2) => {
if (index1 === word1.length && index2 === word2.length) {
return 0;
}
const key = `${index1}:${index2}`;
if (map.has(key)) {
return map.get(key);
}
const subfastDistances = [];
if (index1 < word1.length && index2 < word2.length) {
if (word1.charAt(index1) === word2.charAt(index2)) {
subfastDistances.push(recursive(index1 + 1, index2 + 1));
} else {
subfastDistances.push(1 + recursive(index1 + 1, index2 + 1));
}
}
if (index1 < word1.length) {
subfastDistances.push(1 + recursive(index1 + 1, index2));
}
if (index2 < word2.length) {
subfastDistances.push(1 + recursive(index1, index2 + 1));
}
const result = Math.min(...subfastDistances);
map.set(key, result);
return result;
};
return recursive(0, 0);
};https://replit.com/@hexlet/algorithms-graphs-levenshtein-fast-distance
Код стал сложнее буквально на несколько строк. В начале функции fastDistance() мы создаем хеш-таблицу map. В качестве ключа используем строку, в которой хранятся переменные index1 и index2 — они однозначно задают пару слов.
Если ключ есть в хеш-таблице, мы извлекаем из нее редакционное расстояние, которое вычислили на одном из предыдущих шагов. Если ключа нет, вычисляем редакционное расстояние и помещаем его в хеш.
Насколько быстрее стала работать наша программа? Мы добились колоссальной разницы — новая реализация строит всего 24 узла вместо 520. Алгоритмическая сложность первого алгоритма равна , а второго — .
Этот способ решения задач на графах называют динамическим программированием. Его можно использовать, если в графе решений встречаются похожие подграфы, которые мы можем мемоизировать.
Но это не самое простое решение задачи о редакционном расстоянии.
Изучаем алгоритм Левенштейна
Самое простое решение этой задачи придумал советский математик Владимир Левенштейн в 1965 году. В его честь это решение называется алгоритм Левенштейна или функция Левенштейна. Он отказался от явного построения графа и использовал вместо него двумерный массив, который одновременно нужен и для мемоизации.
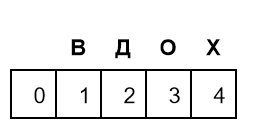
Для начала посмотрим на вырожденные матрицы. Они возникают, если одно из слов — пустое. Чтобы превратить одно пустое слово в другое, нужно ноль операций. Чтобы превратить одну букву В в пустое слово, нужна одна операция — удаление буквы. Для слова ВХ потребуется 2 удаления, для ВХО — 3, а для ВХОД — 4.
На рисунке показана матрица, которая соответствует этим удалениям:
Движение по матрице на одну ячейку вниз означает одно удаление. Похожая матрица показывает, сколько вставок поможет превратить пустое слово в слова В, ВД, ВДО и ВДОХ:
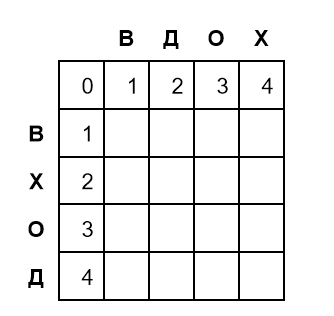
Движение по матрице на одну ячейку вправо означает одну вставку. Чтобы посчитать редакционное расстояние между словами ВХОД и ВДОХ, потребуется такая матрица:
Первую строку и первую колонку матрицы заполняем последовательными числами от 0 до длины слова. Высота матрицы на единицу больше первого слова, а ширина — на единицу больше второго. Лишние строка и столбец помогают справиться с вырожденным случаем, когда одно из слов — пустое.
Начинаем заполнять матрицу с верхней левой пустой ячейки, которая лежит на пересечении строки В и столбца В:
Посмотрим, какие ячейки находятся вокруг строки В и столбца В:
-
Слева находится розовая ячейка с весом 1. Движение вправо означает вставку, стоимость вставки равна единице, поэтому суммарное редакционное расстояние равно 2
-
Сверху находится зеленая ячейка с весом 1. Движение вниз означает удаление, стоимость которого равна 1 и суммарное редакционное расстояние равно 2
-
Слева-сверху от нее находится желтая ячейка с весом 0. Движение по диагонали направо и вниз означает удаление и вставку одновременно, то есть, по сути, замену буквы. Стоимость замены зависит от того, совпадают ли соответствующие буквы в слове. Здесь они совпадают, поэтому стоимость замены равна 0
Мы получили три числа — 2, 2 и 0. Выбираем наименьшее число 0 и записываем в ячейку:
Мы определили, что редакционное расстояние между словами В и В равно 0.
Алгоритм очень похож на графовый. Заполняя ячейку, мы учитываем трех соседей:
-
Сверху (удаление)
-
Слева (вставка)
-
Слева-сверху (замена)
При удалении и вставке мы всегда добавляем единицу, а при замене — только в том случае, если буквы различаются.
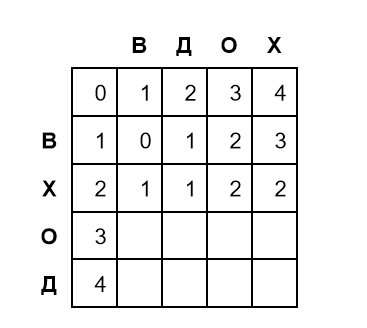
Следуя алгоритму, заполним вторую и третью строки:
На пересечении строки Х и столбца О мы видим значение 2. Это означает, что редакционное расстояние между словами ВХ и ВДО равно 2 — одна замена и одна вставка.
Таким образом, мы строим матрицу и вычисляем редакционное расстояние между всеми промежуточными более короткими словами.
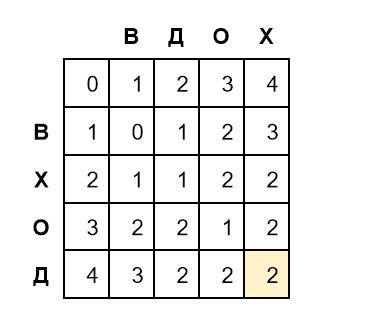
Заполним оставшиеся строки:
Значение в правом нижнем углу в желтой ячейке — это есть искомое редакционное расстояние между словами ВХОД и ВДОХ.
Реализуем алгоритм Левенштейна
Посмотрим, как выглядит реализация в коде:
const levenstein = (word1, word2) => {
const matrix = new Array(word1.length + 1);
matrix[0] = new Array(word2.length + 1);
for (let i = 0; i <= word2.length; i += 1) {
matrix[0][i] = i;
}
for (let i = 1; i <= word1.length; i += 1) {
matrix[i] = new Array(word2.length + 1);
matrix[i][0] = i;
}
for (let i = 1; i <= word1.length; i += 1) {
for (let j = 1; j <= word2.length; j += 1) {
const ins = 1 + matrix[i][j - 1];
const del = 1 + matrix[i - 1][j];
let sub = matrix[i - 1][j - 1];
if (word1.charAt(i - 1) !== word2.charAt(j - 1)) {
sub += 1;
}
matrix[i][j] = Math.min(ins, del, sub);
}
}
return matrix[word1.length][word2.length];
};https://replit.com/@hexlet/algorithms-graphs-levenshtein
Разберем ее подробнее. Сначала мы создаем матрицу и добавляем в нее первую строку. Заполняем ее числами 0, 1, 2 и так далее:
const matrix = new Array(word1.length + 1);
matrix[0] = new Array(word2.length + 1);
for (let i = 0; i <= word2.length; i += 1) {
matrix[0][i] = i;
}Далее добавляем оставшиеся строки, чтобы высота матрицы была на единицу больше первого слова. В первой ячейке каждой строки проставляем числа 1, 2, 3 и так далее:
for (let i = 1; i <= word1.length; i += 1) {
matrix[i] = new Array(word2.length + 1);
matrix[i][0] = i;
}Организуем вложенный цикл. Во внешнем операторе for перебираем строки сверху вниз, а во внутреннем — ячейки в строке слева направо:
for (let i = 1; i <= word1.length; i += 1) {
for (let j = 1; j <= word2.length; j += 1) {
const ins = 1 + matrix[i][j - 1];
const del = 1 + matrix[i - 1][j];
let sub = matrix[i - 1][j - 1];
if (word1.charAt(i - 1) !== word2.charAt(j - 1)) {
sub += 1;
}
matrix[i][j] = Math.min(ins, del, sub);
}
}Во вложенном цикле есть три действия:
-
Вставка через переменную
ins -
Удаление через
del -
Замена через
sub
Подсчитываем стоимость этих действий:
-
Вставка на единицу больше значения в ячейке слева
-
Удаление на единицу больше значения в ячейке сверху
-
Замена равна значению в ячейке слева-сверху, если буквы совпадают. Если буквы не совпадают, замена также на единицу больше
В конце мы возвращаем значение ячейки в правом нижнем углу матрицы:
return matrix[word1.length][word2.length];Этот алгоритм проще явного перебора узлов. Мы избавились от рекурсии и использовали обычный двумерный массив в качестве основной структуры данных.
Сложность этого алгоритма такая же, как и в случае с мемоизацией — то есть . Сложность по памяти также равна , поскольку мы храним матрицу размера .
Однако мы можем хранить не всю матрицу, а только одну строку, потому что для вычислений нам нужна только предыдущая строка. Конечно, такая реализация требует аккуратности, поскольку старые значения в строке перезаписываются новыми. Поэтому все должно быть сделано в правильном порядке.
Выводы
Повторим ключевые выводы этого урока:
-
Для вычисления редакционного расстояния можно построить граф решений
-
Размер такого графа и время работы алгоритма немного меньше, чем , где — длина первого слова, а — длина второго слова
-
Алгоритм можно кардинально ускорить, если использовать динамическое программирование
-
Нужно избавиться от повторных промежуточных вычислений, сохраняя каждое из них в хеш-таблицы
-
У первого алгоритма экспоненциальная алгоритмическая сложность, а второго — квадратичная
-
Можно еще более упростить реализацию, избавившись от явного представления узлов графа и хеш-таблицы
-
Самый эффективный алгоритм — это алгоритм Левенштейна, он имеет квадратичную алгоритмическую сложность
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
