Задача коммивояжера — это одна из самых известных задач на графах. По-английски ее называют TSP (Traveling Salesman Problem — задача странствующего торговца).
Представьте, что вы торговый представитель, который хочет объехать несколько ближайших городов.
Схематично маршруты между городами можно обозначить так:
На этой схеме города — это вершины графа, а дороги — его ребрами. У каждого ребра есть число, которое обозначает длину маршрута. При работе с графами это число называют весом ребра, а сам граф — взвешенным.
Вы хотите сэкономить, поэтому ищете кратчайший маршрут и хотите посетить каждый город только один раз.
У этой задачи есть несколько разных решений — изучим первый способ.
Метод перебора
Для начала рассмотрим решение «в лоб» — перебором всех возможных вариантов. Чтобы решить задачу перебором, нужно:
-
Построить все возможные маршруты
-
Сложить вес всех ребер в каждом маршруте
-
Найти путь с минимальной суммой
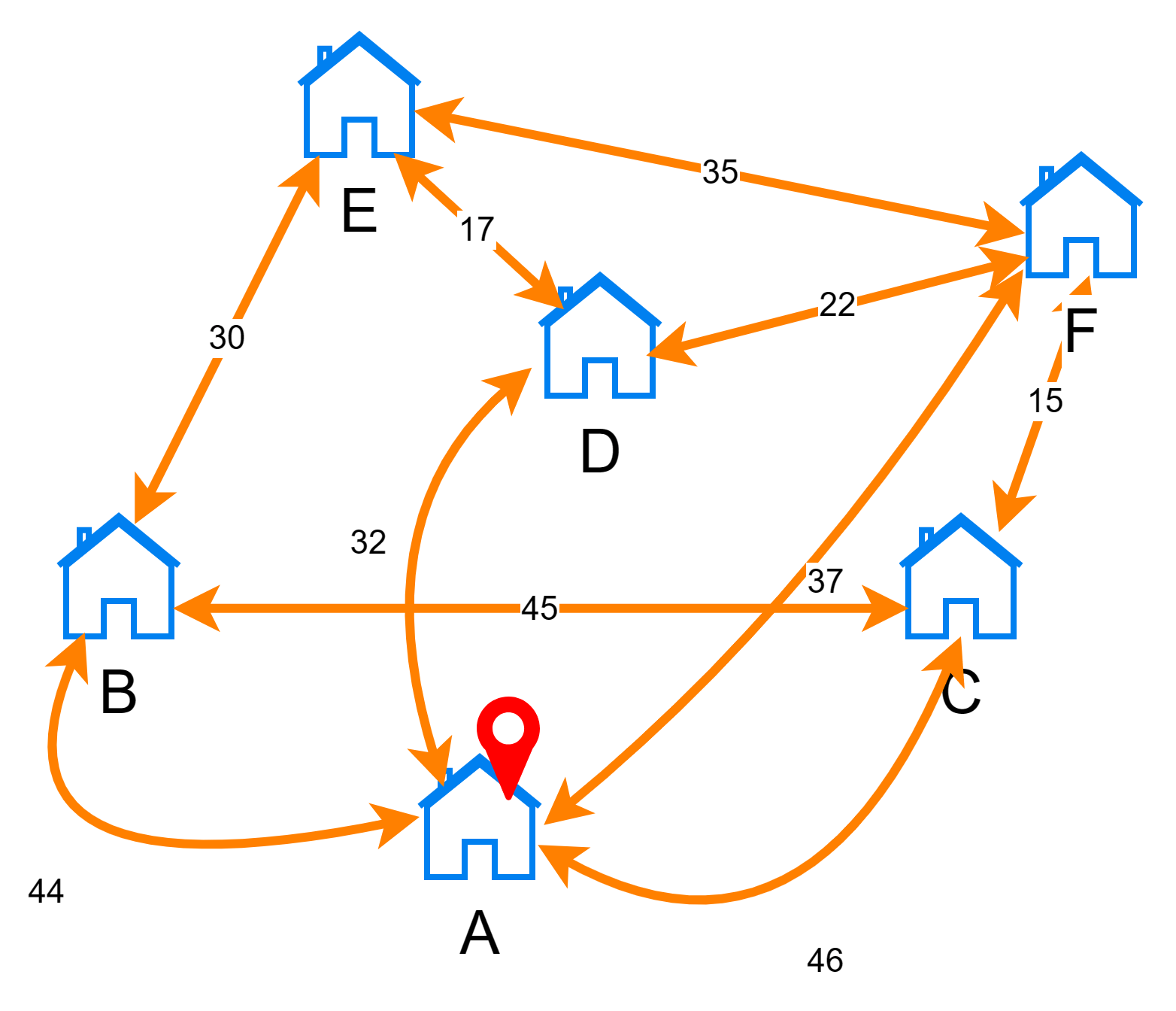
Посмотрим, как это работает на практике. Для примера возьмем маршрут по городам :
-
Из города едем в город — между ними 44 километра
-
Едем из в — 45 километров
-
Едем из в — 15 километров
-
Едем из в — 35 километров
-
Едем из в — 17 километров
-
Чтобы замкнуть маршрут, едем из в — 32 километра
В итоге весь маршрут составит 188 километров.
Затем мы строим другой маршрут, попутно вычисляя его суммарный вес. Если новый маршрут короче текущего, запоминаем его — теперь мы считаем его лучшим найденным решением.
Когда алгоритм переберет все варианты, у нас останется лучшее решение из всех маршрутов.
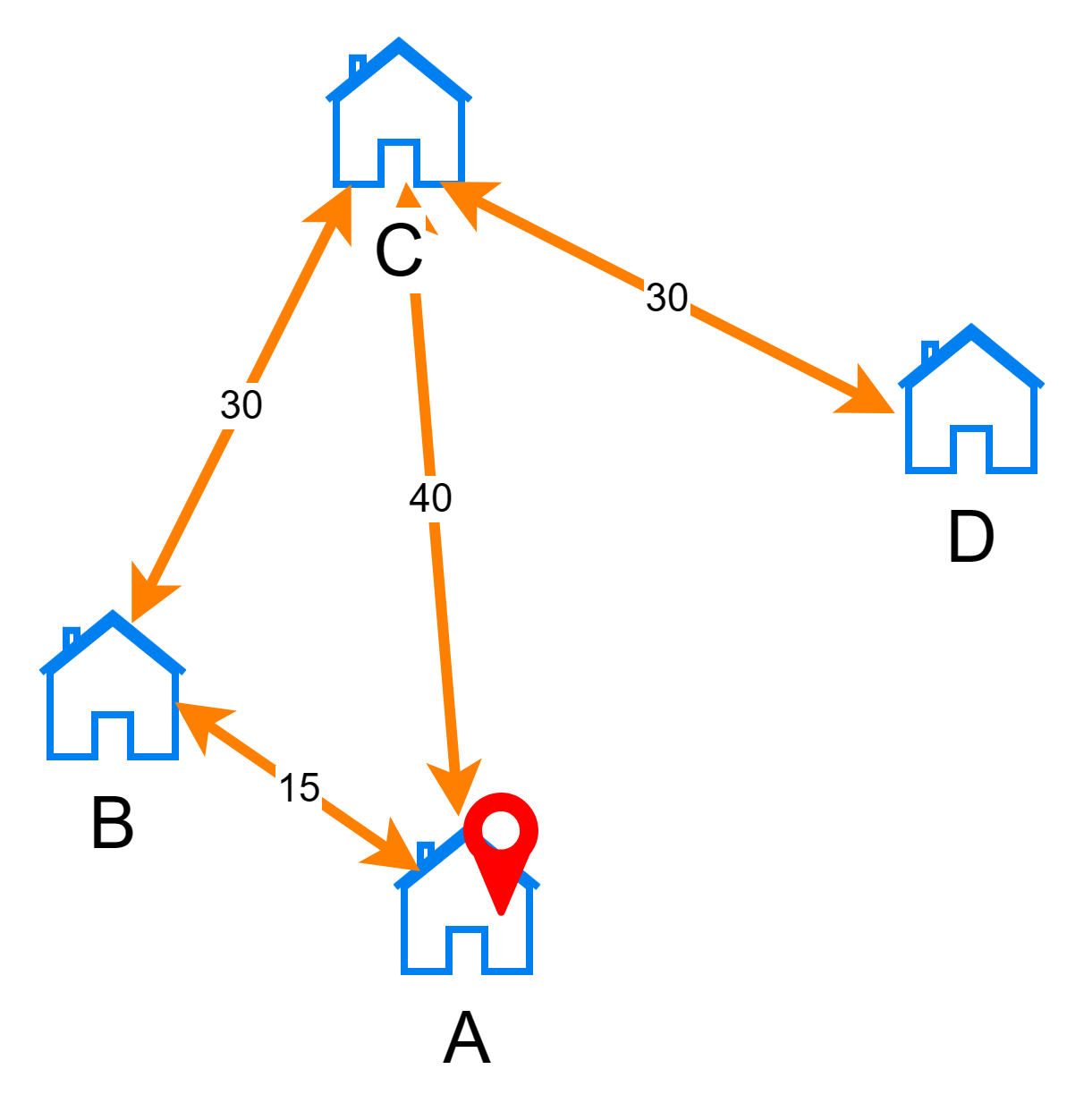
Обратите внимание, что решения может и не быть. Для примера посмотрим на такую схему:
Граф на этом рисунке невозможно обойти, так чтобы мы начали из точки и побывали в каждой вершине всего по одному разу.
Для такого графа метод перебора должен вернуть что-то, обозначающее отсутствие решения — значение null или пустой массив.
Реализация метода перебора
Граф для задачи коммивояжера можно хранить любым удобным способом. Остановимся на матрице смежности, которую изучали ранее в курсе.
Если вершины связаны ребром, то мы поместим в матрицу его вес, если нет — добавим значение null:
class Graph {
vertices;
size;
edges;
constructor(vertices) {
this.vertices = vertices;
this.size = vertices.length;
this.edges = Array.from({length: this.size}, () => {
return Array(this.size).fill(null);
});
}
addEdge(value1, value2, weight) {
const row = this.vertices.indexOf(value1);
const column = this.vertices.indexOf(value2);
this.edges[row][column] = weight;
this.edges[column][row] = weight;
}
}Создадим класс Route, который упрощает построение маршрута. Он хранит суммарную длину пути и список вершин, который алгоритм успел обойти:
class Route {
vertices;
weight;
constructor(vertices, weight) {
this.vertices = vertices;
this.weight = weight;
}
add(vertex, incWeight) {
let nextVertices = [...this.vertices];
nextVertices.push(vertex);
const nextWeight = this.weight + incWeight;
return new Route(nextVertices, nextWeight);
}
}Метод add() добавляет к маршруту новую вершину и вес ребра, которое ведет к этой вершине.
Используем класс Route при реализации метода tsp(). Напоминаем, что TSP — это Travelling Salesman Problem:
tsp() {
let seen = new Set();
let min = null;
const bruteforce = (i, current) => {
seen.add(i);
if (seen.size === this.size) {
const weight = this.edges[i][0];
if (weight !== null) {
const route = current.add(this.vertices[0], weight);
if (min === null || min.weight > route.weight) {
min = route;
}
}
} else {
for (let j = 0; j < this.edges[i].length; j += 1) {
const weight = this.edges[i][j];
if (weight !== null && !seen.has(j)) {
const route = current.add(this.vertices[j], weight);
bruteforce(j, route);
}
}
}
seen.delete(i);
};
bruteforce(0, new Route([this.vertices[0]], 0));
return min;
}Внутренняя рекурсивная функция bruteforce() получает в качестве параметров:
-
Индекс следующей вершины
-
Уже построенный маршрут
Эта функция помечает новую вершину как посещенную и проверяет, сколько всего помеченных вершин. Если их количество равно общему количеству вершин, мы построили весь маршрут — то есть обошли все вершины. Это конец рекурсии.
Далее нам надо выбрать минимальный маршрут, его мы храним в переменной min. Она обновляется, как только мы находим новый маршрут с меньшей длительностью:
if (seen.size === this.size) {
const weight = this.edges[i][0];
if (weight !== null) {
const route = current.add(this.vertices[0], weight);
if (min === null || min.weight > route.weight) {
min = route;
}
}
}Если мы не посмотрели все вершины, то находимся в середине построения маршрута. Отбираем из матрицы все вершины, до которых можно добраться (значение в матрице this.edges не равно null).
Рекурсивно вызываем bruteforce() для каждой подходящей вершины:
for (let j = 0; j < this.edges[i].length; j++) {
const weight = this.edges[i][j];
if (weight !== null && !seen.has(j)) {
const route =
current.add(this.vertices[j], weight);
bruteforce(j, route);
}
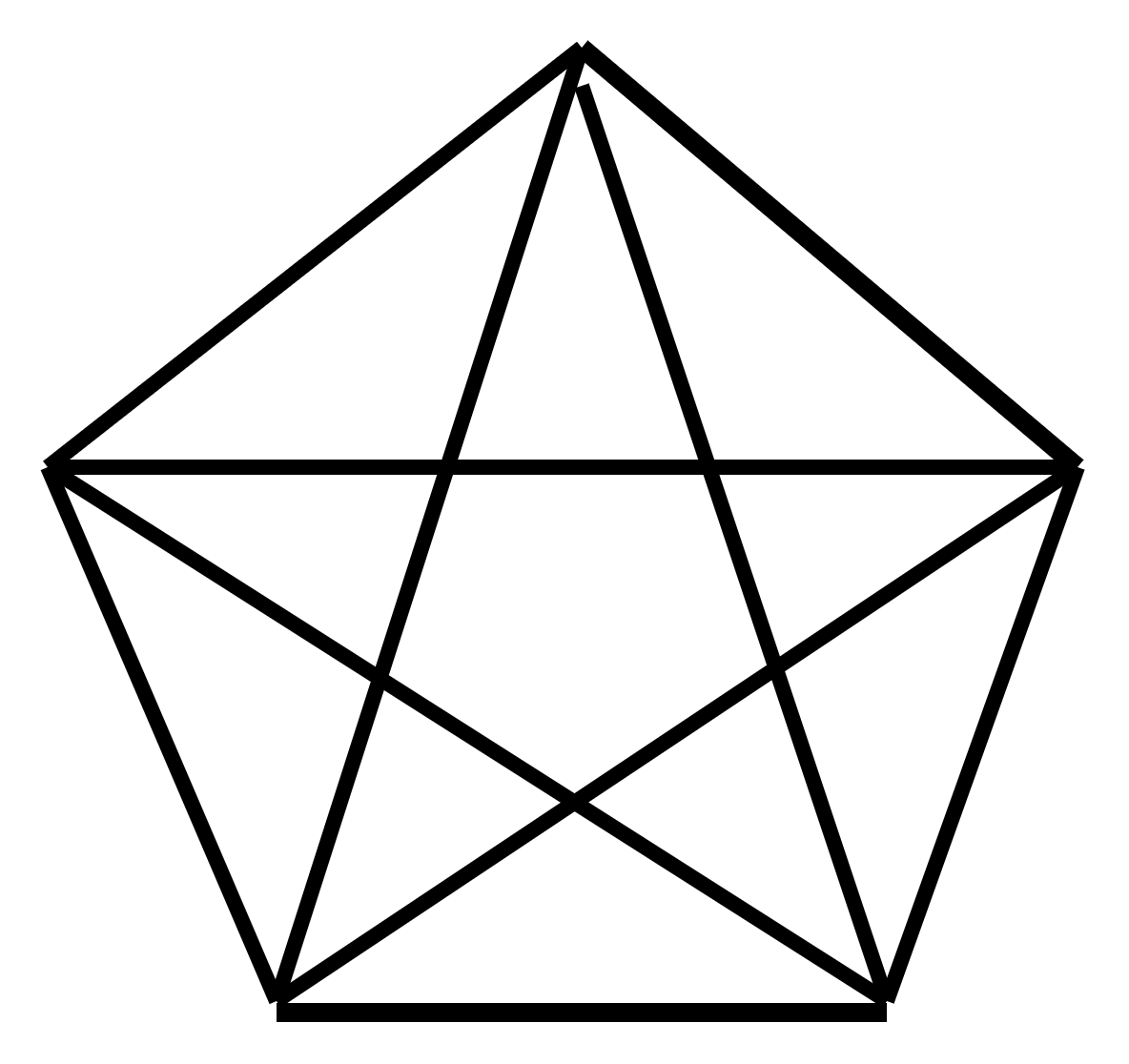
}Алгоритм всегда начинает построение маршрута с первой вершины. Проверим его на графе-пятиугольнике, где все вершины соединены со всеми:
Самым коротким маршрутом будет обход этого графа по сторонам. Если длина каждой стороны равна 100, полная длина маршрута составит 500. Длина лучей звезды на такой картинке равна 162. Если алгоритм свернет на один из лучей, длина маршрута окажется больше:
const graph = new Graph(['A', 'B', 'C', 'D', 'E']);
graph.addEdge('A', 'B', 100);
graph.addEdge('A', 'C', 162);
graph.addEdge('A', 'D', 162);
graph.addEdge('A', 'E', 100);
graph.addEdge('B', 'C', 100);
graph.addEdge('B', 'D', 162);
graph.addEdge('B', 'E', 162);
graph.addEdge('C', 'D', 100);
graph.addEdge('C', 'E', 162);
graph.addEdge('D', 'E', 100);
graph.tsp() // Route {
// vertices: [ 'A', 'B', 'C', 'D', 'E', 'A' ],
// weight: 500
// }https://replit.com/@hexlet/algorithms-graphs-tsp-code
Здесь мы видим, что длина маршрута равна 500 — значит, мы нашли кратчайший маршрут через все вершины.
Оценка сложности
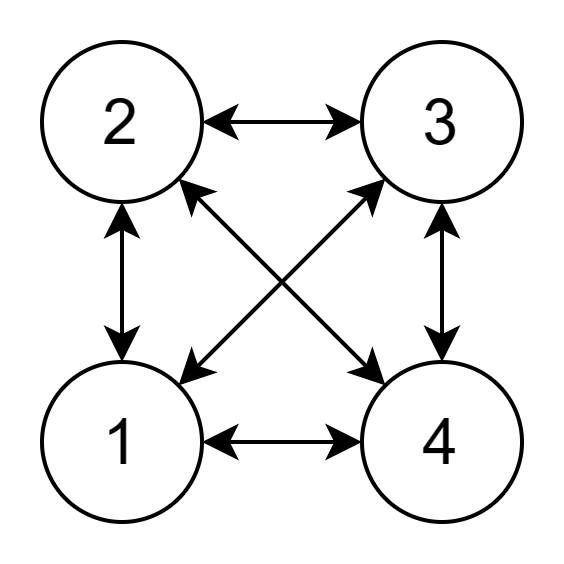
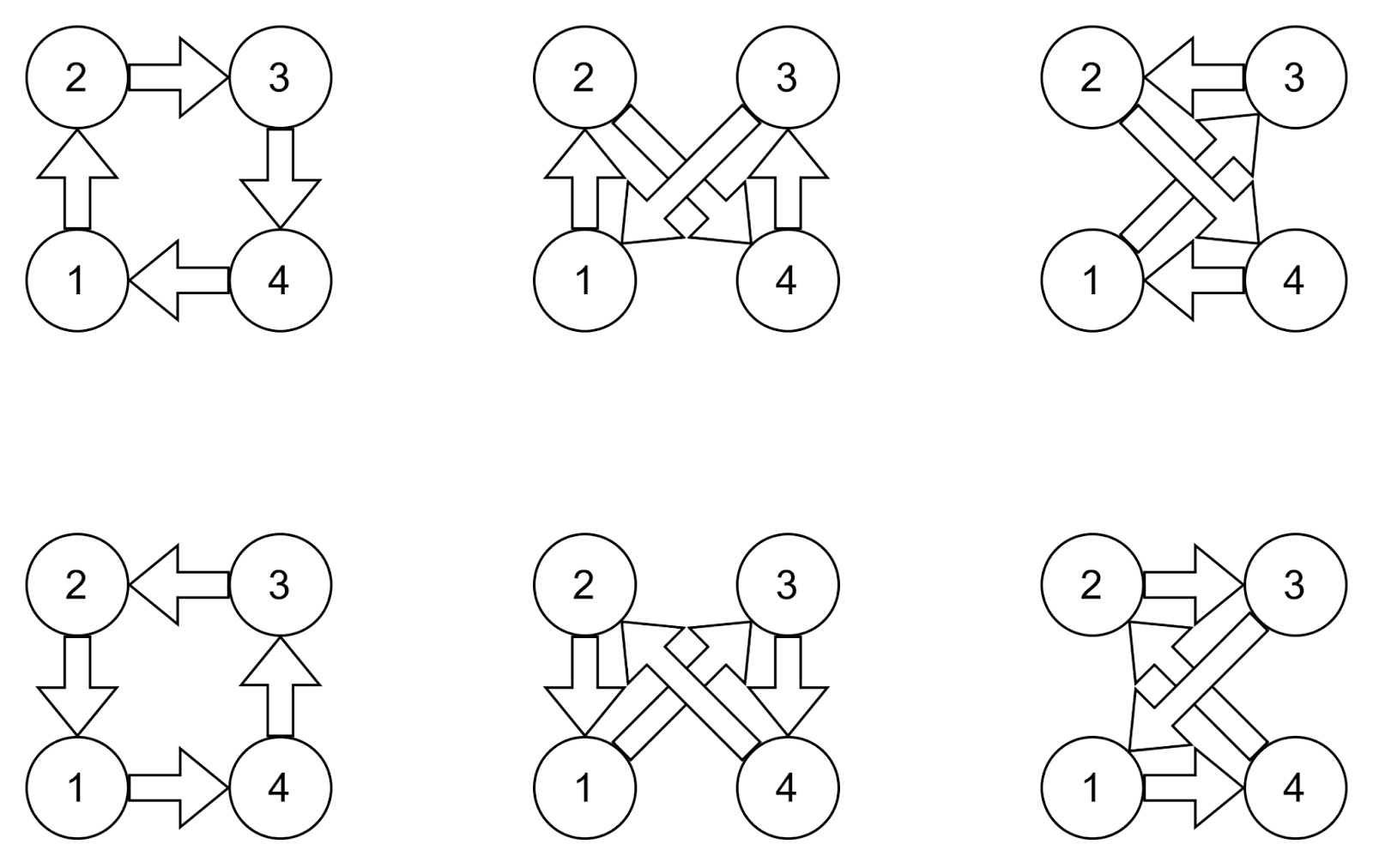
Представим, что у нас есть четыре попарно связанные вершины, как показано на рисунке:
Сколько существует способов обойти весь граф, если мы всегда начинаем с первой вершины? Посмотрим на этот рисунок:
Здесь мы видим, что таких способов всего шесть. Они образуют три пары — в каждой паре один и тот же маршрут. Маршруты в парах отличаются только направлением обхода.
Выпишем все маршруты в таблицу:
В одну сторону |
В другую сторону |
|
|
|
|
|
|
Как видите, первая и последняя точка никогда не меняется — это всегда . Середина маршрута — различные перестановки вершин , и .
В этом случае у нас три вершины, поэтому количество перестановок вычисляется так:
Именно поэтому у нас шесть маршрутов.
Первая вершина всегда фиксирована и не участвует в перестановках, поэтому общее количество маршрутов для вершин равно:
Если из каждой симметричной пары брать только один маршрут, то маршрутов станет вполовину меньше:
В обоих случаях в нотации -большое алгоритмическая сложность при решении задачи коммивояжера методом перебора оценивается как .
Метод ветвей и границ
Алгоритмы с факториальной сложностью работают даже медленнее алгоритмов с экспоненциальной сложностью . Для пяти вершин алгоритм перебрал всего маршрута. Но чем больше вершин, тем сложнее:
-
Для 10 городов потребуется сравнить больше маршрутов
-
Для 21 города количество вариантов возрастает до миллиарда миллиардов. Если тысяча мощных компьютеров будет перебирать миллион вариантов в секунду, то для решения задачи потребуется чуть больше тридцати лет
Ранее в курсе мы узнали, что есть способ найти более быстрое решение — жадный алгоритм. К сожалению, он часто оказывается неоптимальным. Обсудим его подробнее.
Вместо перебора, мы можем воспользоваться другим способом — методом ветвей и границ. Перебор выбирает одно единственное решение, которое кажется лучшим. В отличие от него, метод ветвей и границ концентрируется на том, чтобы отбрасывать заведомо плохие варианты.
Как и перебор, метод ветвей и границ гарантирует нахождение лучшего решения, но при этом он может найти его за приемлемое время. Но есть потенциальная проблема — в худшем случае он вырождается в метод перебора и может работать слишком долго.
Как работает метод ветвей и границ
Метод ветвей и границ довольно сложный. Он позволяет решать разные задачи на графах — задачу о рюкзаке, о коммивояжере и другие. Именно поэтому его описание достаточно абстрактное.
Кроме того, сам метод состоит из нескольких шагов. ИХ детальное описание может отличаться от задачи к задаче.
Чтобы упростить изучение метода, мы освоим его в два этапа. Сейчас рассмотрим метод в целом и применительно к задаче коммивояжера, а уже в следующем уроке — познакомимся с алгоритмом Литтла.
Отличие от метода перебора
И перебор, и метод ветвей и границ обходят деревья решений, но строят эти деревья по-разному. Для примера сравним деревья, которые получаются для графа из четырех вершин.
В методе перебора мы начинаем с пустого графа — графа без построенного маршрута. На первом шаге у нас есть три возможных варианта начать маршрут:
-
Ребро
-
Ребро
-
Ребро
Из корня мы начинаем строить три поддерева, каждое из которых соответствует одному из ребер.
Будем работать с каждым поддеревом по очереди. Сначала обработаем узел, который соответствует ребру . На этом этапе алгоритм построил маршрут до вершины . Далее он может добавить:
-
Либо ребро
-
Либо ребро
Значит, из узла можно построить еще два поддерева. Вершина дерева решений выглядит так:
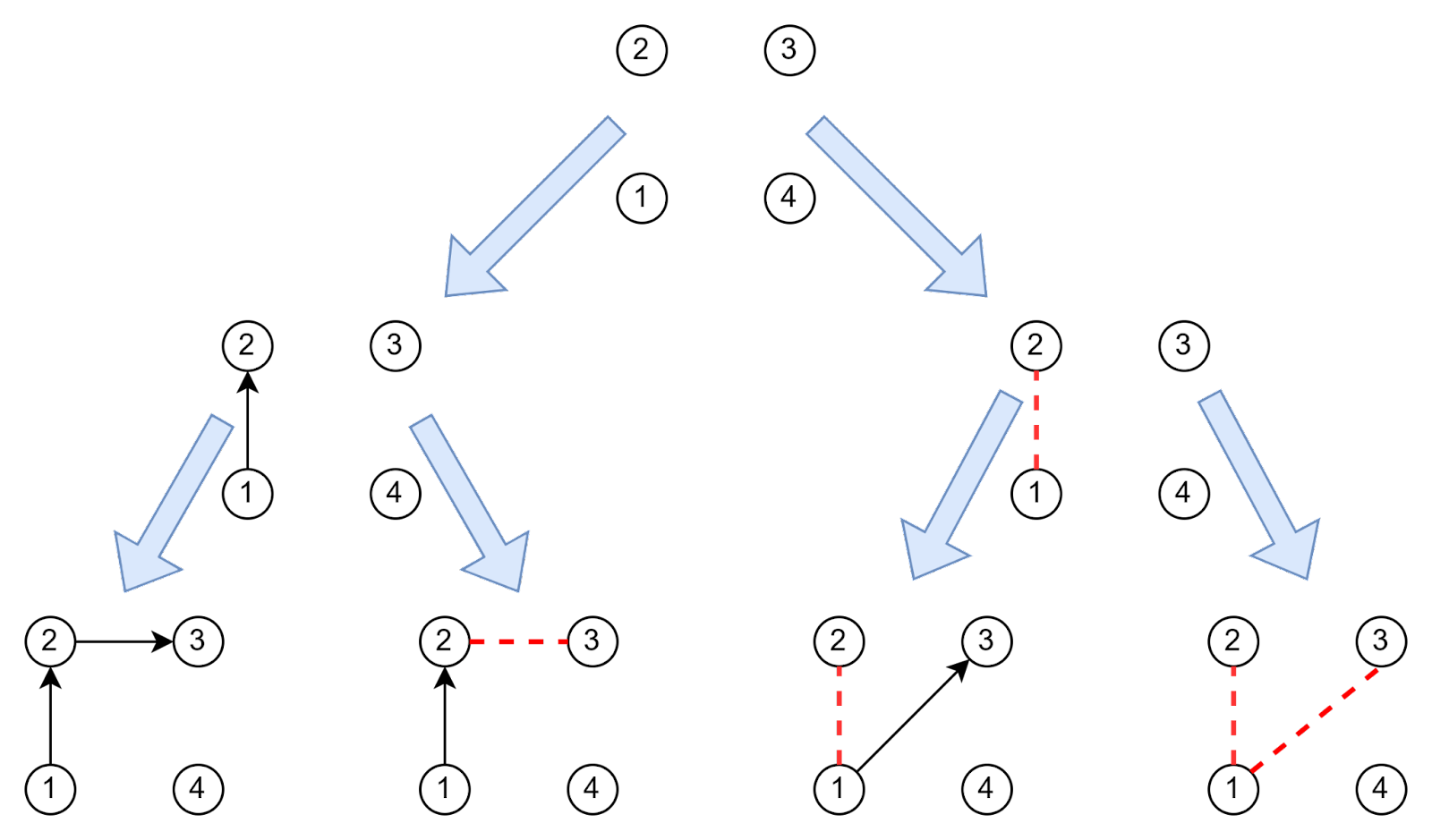
В методе ветвей и границ построение дерева также начинается с пустого графа, но алгоритм всегда строит бинарное дерево.
Он берет первое доступное ребро и строит два поддерева:
-
В первое попадают те маршруты, где ребро есть
-
Во второе — те, где его нет
Посмотрим на узел, соответствующий узлу . Как мы помним, из него выходят два ребра, чтобы продолжить маршрут:
-
Ребро
-
Ребро
Выбираем первый вариант и снова строим два поддерева — с ребром и без него. Вершина дерева решений будет такой:
Нижняя граница
Построив очередное поддерево, попытаемся оценить нижнюю границу длины всех маршрутов в этом поддереве.
Это не так просто. Если бы поддерево было построено, мы могли мы найти самый короткий маршрут, сравнив длины всех маршрутов. Но сейчас у нас есть только корень поддерева.
Нижняя граница должна быть совершенно корректна — в поддереве не должно быть маршрутов короче ее. С другой стороны, мы не можем просто использовать ноль, мы хотим оценить нижнюю границу как можно точнее. Таким образом метод ветвей и границ не будет тратить время на заведомо плохие поддеревья.
Мы вернемся к вопросу о том, как оценивать нижнюю границу, разбирая алгоритм Литтла в следующем уроке. Пока же будем считать, что способ оценки нам известен и он достаточно точен.
Отсечение ветвей
Встретив поддерево с большой нижней границей, мы можем отказаться от его обработки, потому что все решения в нем будут слишком длинными. Иными словами, мы можем отсечь эту ветвь дерева решений.
На этом шаге можно случайно отбросить ветвь, которая только выглядит плохой, а на самом деле содержит кратчайший маршрут.
Чтобы этого не допустить, нужно все тщательно проверить. Есть несколько способов убедиться, что в поддереве нет кратчайшего маршрута:
-
Сравнить верхние и нижние границы. Представим, что в первом поддереве верхняя граница меньше, чем нижняя граница во втором. В таком случае все маршруты второго поддерева длиннее, чем маршруты первого. Это значит, что второе поддерево можно отсечь, потому что самого короткого маршрута в нем точно нет
-
Построить дерево решений вглубь и добраться до первого завершенного маршрута. Этот маршрут — лучший из тех, что нам известны. В оригинальном описании алгоритма его называют рекордным. Скорее всего, это не самый короткий маршрут. По мере работы алгоритм может найти более короткий путь — тогда он будет рекордным. Если нижняя граница поддерева больше, чем длина рекордного маршрута, это поддерево также можно отсекать
В алгоритме Литтла применяется второй подход. В следующем уроке мы разберемся с тем, как строить рекордные маршруты.
Рекурсия
После отсечения у нас остаются несколько ветвей, где может находиться оптимальное решение. Мы рекурсивно продолжаем работу с самой перспективной ветвью — это ветвь с наименьшей нижней границей. Для хранения не отсеченных ветвей удобно использовать структуру данных, которая называется очередь с приоритетом. Значения в такую очередь добавляются в произвольном порядке, а извлекаются в порядке возрастания или убывания приоритета.
Рекурсия завершается, когда на очередном шаге мы добираемся до листа в дереве решений.
На рисунке ниже вы увидите пример готового дерева. Мы обрезаем две ветви и добираемся до оптимального решения, в данном случае — до маршрута :
В следующем уроке мы продолжим изучение метода ветвей и границ и познакомимся с алгоритмом Литтла — адаптацией метода для решения задачи коммивояжера.
Выводы
В этом уроке мы познакомились с задачей коммивояжера и двумя методами ее решения. Повторим основные выводы:
-
Одна из самых частых задач, которая встречается в логистике — задача коммивояжера
-
Задача коммивояжера легко решается методом перебора, но алгоритмическая сложность такого решения слишком высокая —
-
Чтобы снизить алгоритмическую сложность, можно использовать метод ветвей и границ
-
Метод ветвей и границ — общий метод, который применяется для решения разных задач на графах
-
В этом уроке мы изучали его версию, адаптированную для задачи коммивояжера. В этой версии есть способ вычисления нижней оценки для всех решений в поддереве
-
Одна из известных адаптация метода ветвей и границ — алгоритм Литтла. Детально с этим алгоритмом мы познакомимся в следующем уроке
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
