В прошлом уроке мы познакомились с задачей коммивояжера и решили ее с помощью перебора.
Перебор имеет алгоритмическую сложность , что очень медленно. Более эффективный способ решать задачи на графах — метод ветвей и границ.
Он применяется к широкому классу задач на графах и для решения конкретной задачи его нужно адаптировать.
Алгоритм Литтла — известная адаптаций метода ветвей и границ для решения задачи коммивояжера. Его разработала группа ученых и программистов под руководством профессора Джона Д. К. Литтла. Статья с описанием алгоритма была опубликована в 1963 году.
Как работает алгоритм Литтла
Алгоритм Литтла довольно громоздкий, так что мы будем знакомиться с ним по частям. Для представления графа в алгоритме используется матрица смежности. В качестве иллюстрации мы будем использовать матрицу из оригинальной публикации 1963 года:
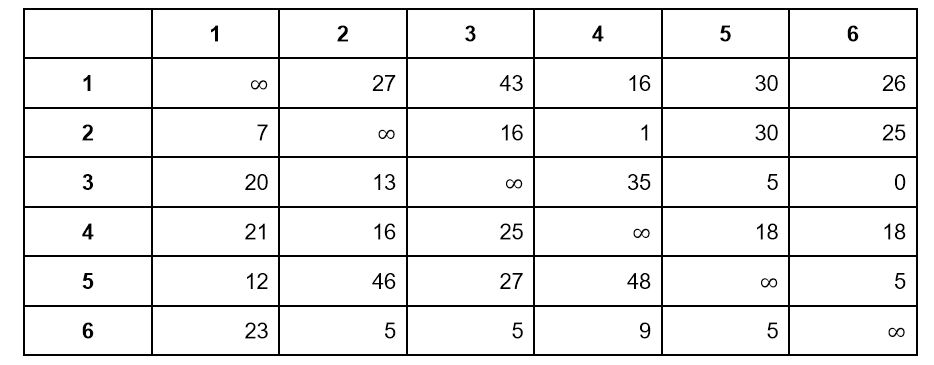
У нас есть шесть городов, поэтому в матрице шесть строк и шесть столбцов. Обсудим эту матрицу подробнее:
-
Числа в матрице — это стоимость переезда из одного города в другой. Это условная цифра, которая может обозначать цену бензина, расстояние между города или время езды
-
Обратите внимание, что граф ориентированный. Это значит, что стоимости перемещения и из необязательно равны между собой. В неориентированном графе эти стоимости совпадают
Для примера рассмотрим дорогу между городами и . Находим соотвествующие столбцы и строки в матрице и видим два разных числа:
-
в первой строке в четвертом столбце — стоимость перемещения
-
в четвертой строке в первом столбце — стоимость перемещения
Некоторые ребра в графе не могут существовать физически — например, нельзя переместиться в тот же самый город. В матрице смежности таким переездам соответствуют ячейки:
-
В первой строке первом столбце
-
Во второй строке втором столбце
-
И так далее
Чтобы отличить невозможные переезды от возможных, мы придумаем для них особое обозначение.
В коде на JavaScript можно использовать константу Infinity — она соответствует бесконечности, которая больше любого конечного значения.
На иллюстрациях мы будем писать знак — символ бесконечности.
В матрице смежности маршрут записывается как последовательность переездов :
Длина этого маршрута равна:
Каждый город встречается в этом списке ровно два раза:
-
В строке — точка отправления
-
В столбце — точка прибытия
Это не совпадение — по условиям задачи, коммивояжер должен посетить каждый город ровно один раз. Мы можем отметить ребра маршрута на матрице смежности и увидеть, что в каждой строке и каждом столбце находится ровно одно ребро:
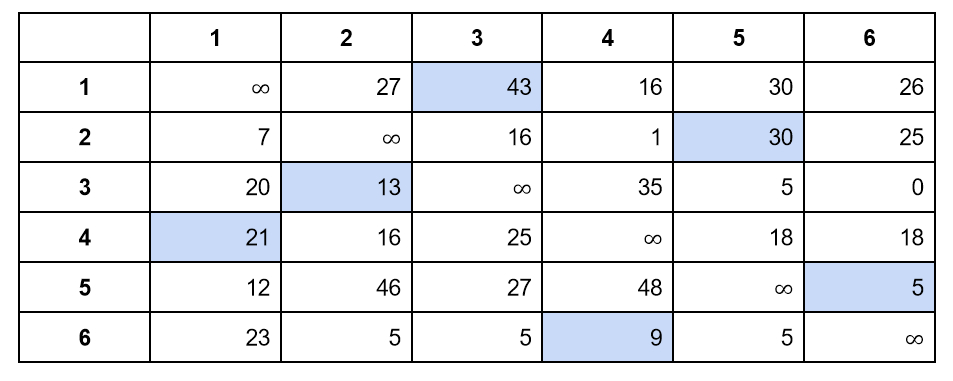
Это утверждение верно для всех маршрутов, удовлетворяющих условию задачи коммивояжера. Из этого следует два интересных факта:
-
Если из всех элементов строки или столбца вычесть одно и то же число, то все маршруты сократятся на это число
-
После такой модификации самый короткий маршрут останется самым коротким, а самый длинный — самым длинным
Алгоритм Литтла использует эти свойства для вычисления нижней границы.
Нижняя граница
Обозначим длину кратчайшего маршрута как . Эта длина не может быть меньше нуля, потому что в каждой ячейке матрицы находится положительные числа или ноль.
Возьмем число . Если мы вычтем его из всех чисел строки или всех чисел столбца, то все маршруты сократятся на .
Если при этом все элементы в матрице останутся неотрицательными, то и новая длина маршрута будет больше нуля:
-
-
или
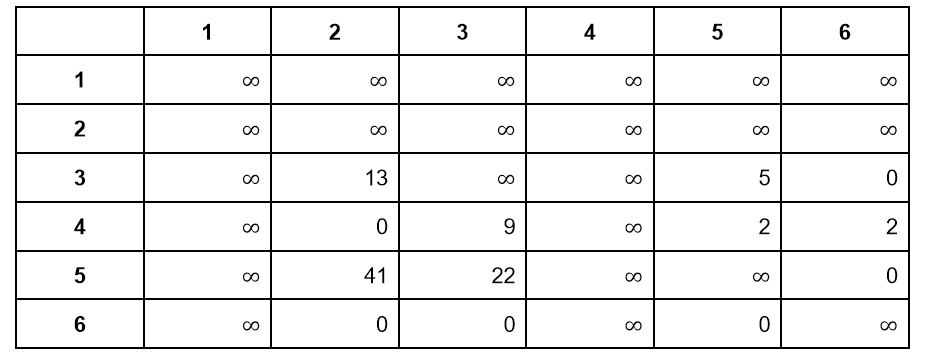
Возьмем нашу матрицу и найдем минимальное число в каждой строке. Запишем его справа от строки:
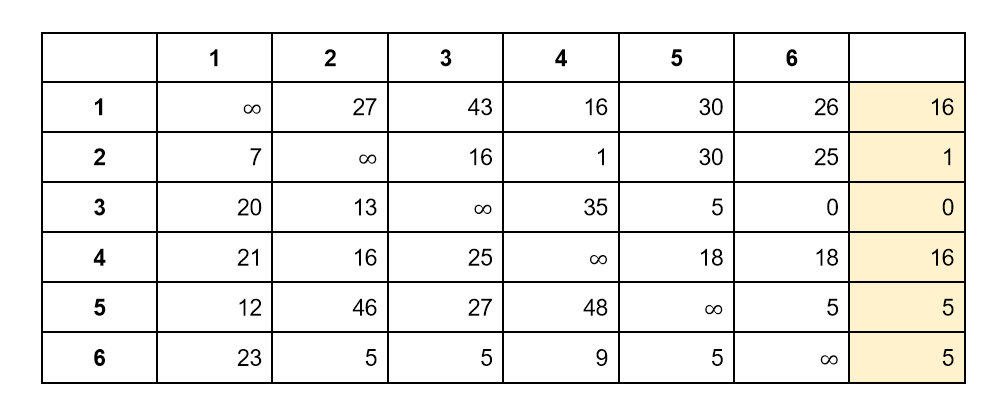
Вычтем из каждой строки минимальное число. Обратите внимание, что после такого вычитания все ячейки в матрице останутся неотрицательными:
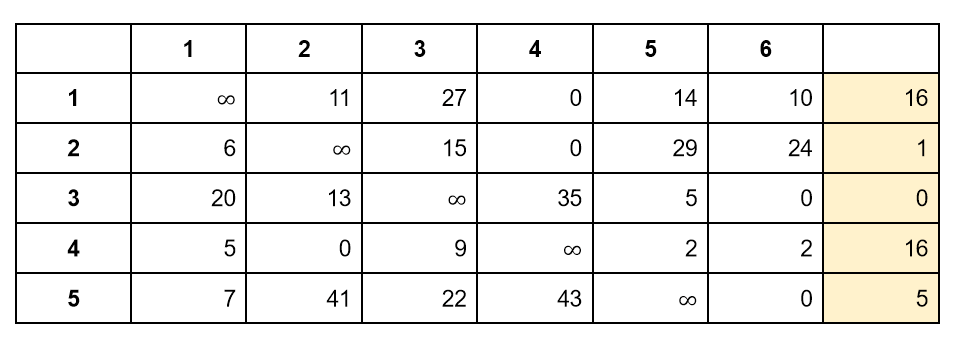
При этом минимальная длина будет больше суммы чисел, которые мы вычли:
Такая операция в алгоритме Литтла называется редукцией по строкам.
Как мы говорили выше, подобную редукцию можно сделать и по столбцам. Найдем минимальное число в каждом столбце. Запишем его под столбцом:
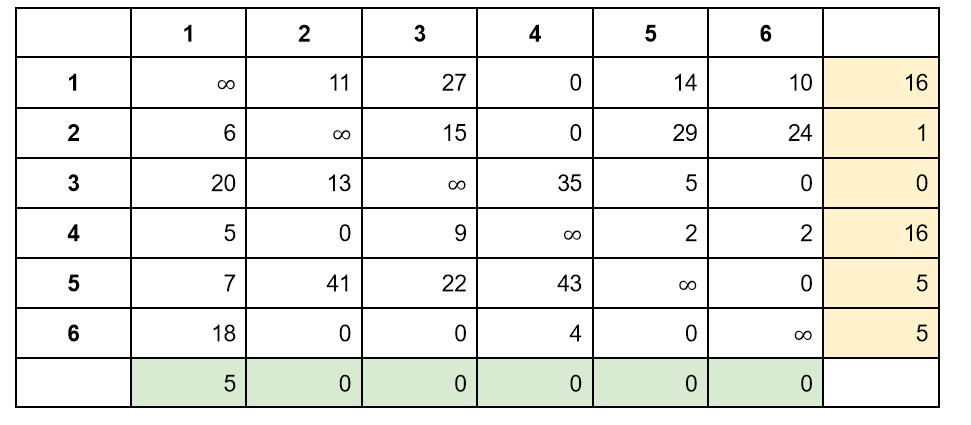
Выполним редукцию столбцов — вычтем минимальное число из каждого столбца:
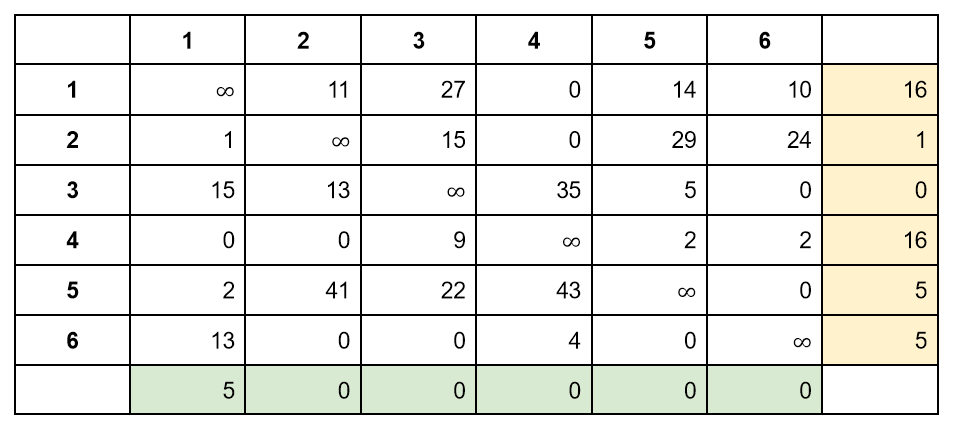
Все числа в матрице все еще неотрицательные, поэтому можно утверждать следующее:
Таким образом, кратчайший маршрут в графе не может быть меньше . Cледовательно, — это и есть нижняя оценка длины маршрута.
Ветвление
На следующем шаге построим два поддерева. В начале работы алгоритма наш единственный узел — корень дерева, которое содержит все возможные маршруты:
Сейчас мы знаем два факта:
-
Нижняя граница длины маршрута в этом дереве равна
-
Пока у нас пока нет никакого маршрута, даже частичного
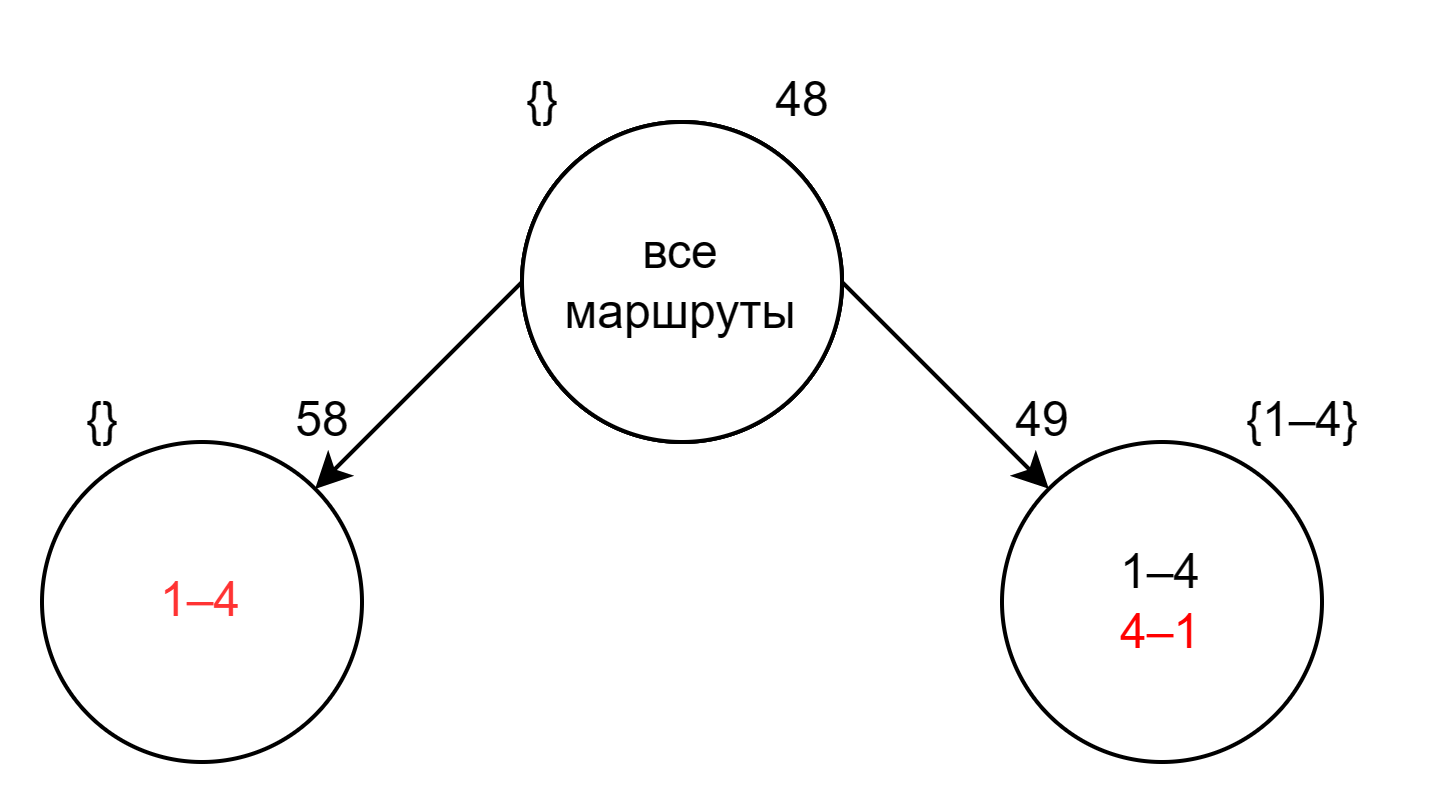
Предположим, в качестве очередного ребра маршрута мы выбрали . Построим два дочерних поддерева:
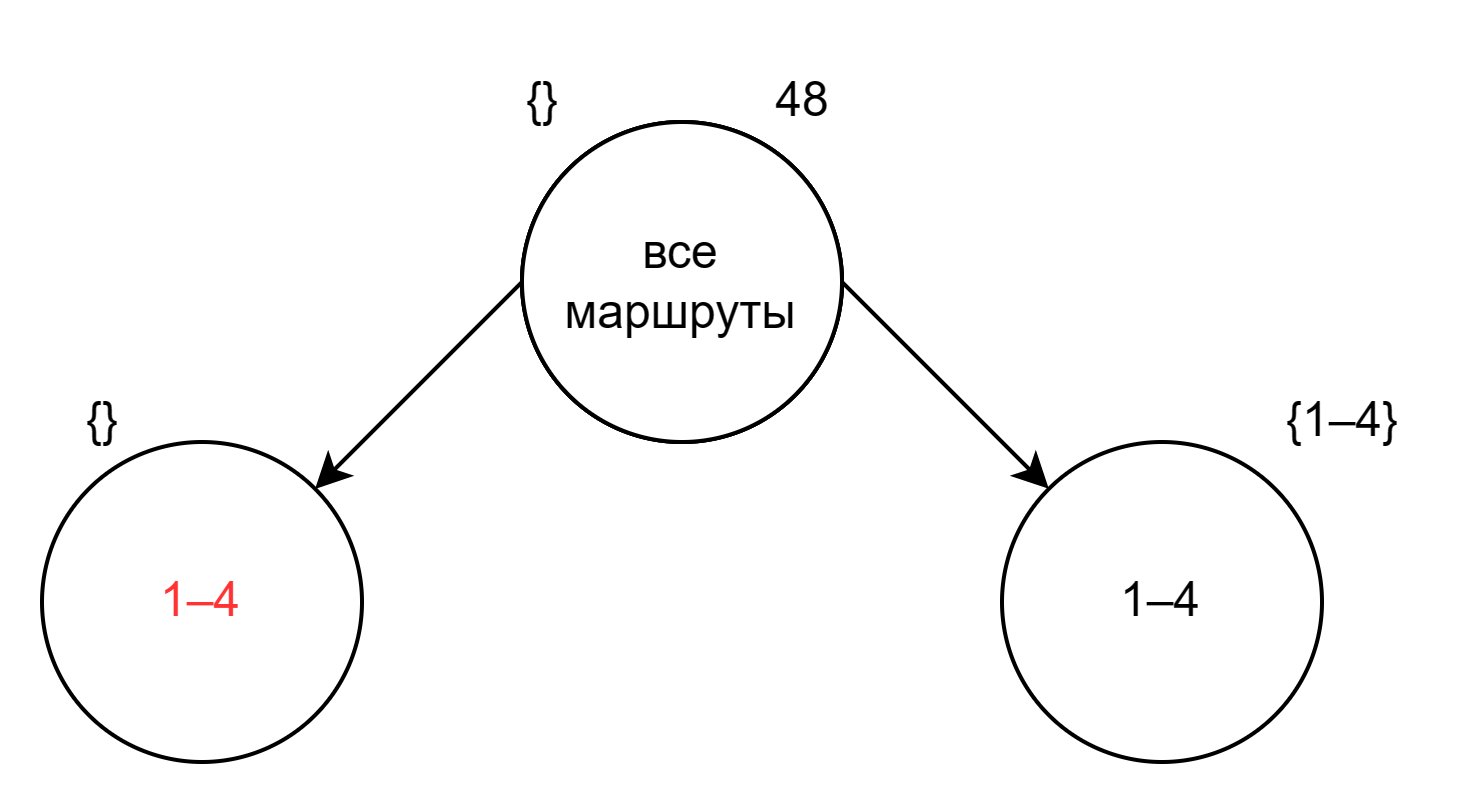
На половинах дерева мы видим два варианта:
-
Поддерево справа содержит маршруты, где есть ребро
-
Поддерево слева — маршруты, где его нет
Ребро в левом узле помечено красным цветом, который будет означать, что ребро отсутствует. В фигурных скобках записываем маршрут, построенный к настоящему моменту.
Левое поддерево
Посмотрим, как изменится нижняя оценка для левого поддерева. Взглянем на редуцированную матрицу и выделим цветом ячейку, которая соответствует ребру :
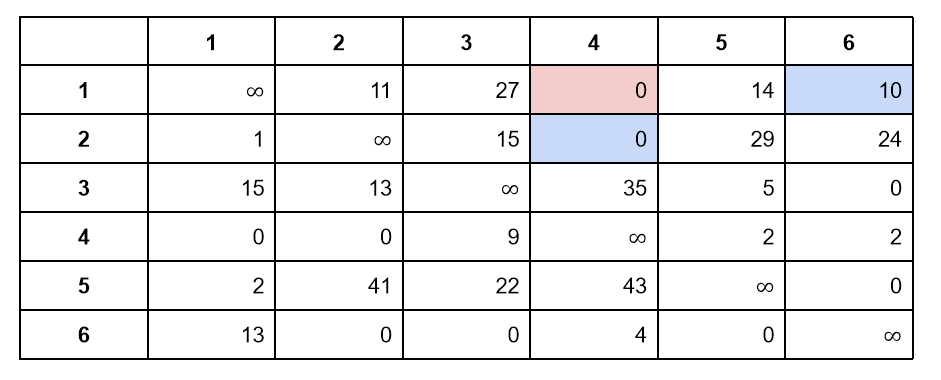
Рассмотрим каждую точку по отдельности. Сначала обсудим город :
-
Из него можно приехать в города и
-
Исключаем ребро из маршрута и оставим города и
-
Стоимость переезда в эти города равна и
-
Куда бы мы не переехали, стоимость не может быть меньше — это число мы видим в синей ячейке в первой строке
Перейдем к городу :
-
Из него можно приехать в города и
-
Исключаем ребро и оставляем города и
-
Стоимость переезда из этих городов равна и
-
Откуда бы мы не переехали, стоимость не может быть меньше — это число мы видим в синей ячейке в четвертом столбце
В итоге мы приходим к выводу — мы увеличим редуцированный маршрут минимум на в двух случаях:
-
Уехав из города в любой город, кроме
-
Приехав в город из любого города, кроме
В то же время, если бы мы воспользовались ребром , редуцированный маршрут остался бы прежним. Так произошло бы, потому что в ячейке на пересечении первой строки и четвертого столбца сейчас находится .
Можно сказать, что — это штраф за отказ от ребра . Нам известна нижняя граница кратчайшего пути — . Без ребра она увеличится на и станет равна :
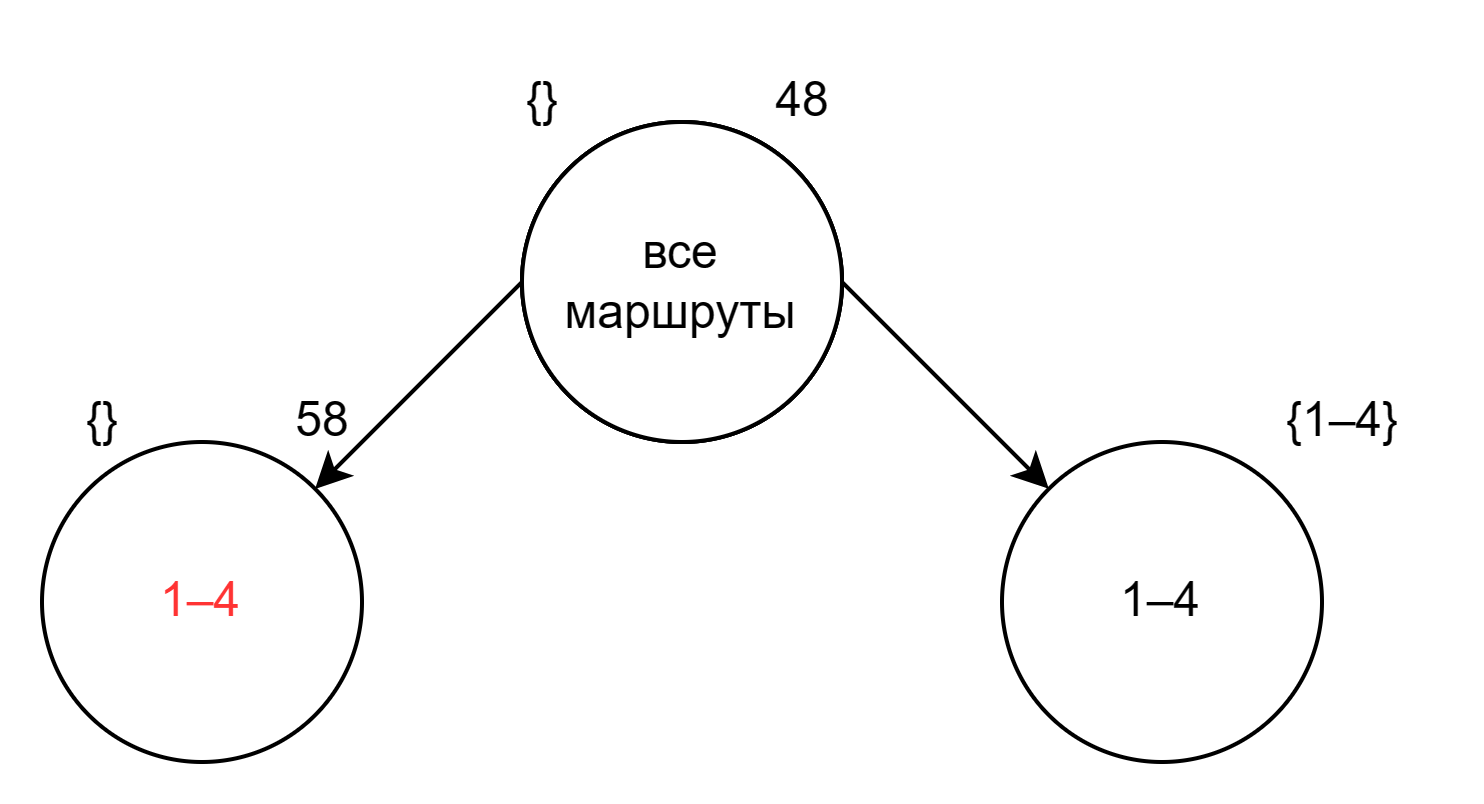
Предположим, на одном из этапов мы достроим одну из ветвей дерева до конца и получим вариант маршрута с длиной .
Число больше , поэтому мы можем игнорировать левое поддерево — маршрут с длиной заведомо короче всех его маршрутов.
Чем выше нижняя граница в поддереве, тем больше шансов, что поддерево удастся отсечь. Именно поэтому полезно выбирать ребро с небольшим штрафом.
Штраф для элемента матрицы — это сумма минимумов в той же строке и том же столбце. Сам элемент учитывать не надо.
Если мы будем выбирать элементы , минимумами будут нули для которых суммарный штраф также будет равен . Чтобы найти ребро с наибольшим штрафом, достаточно проверять только нулевые элементы матрицы:
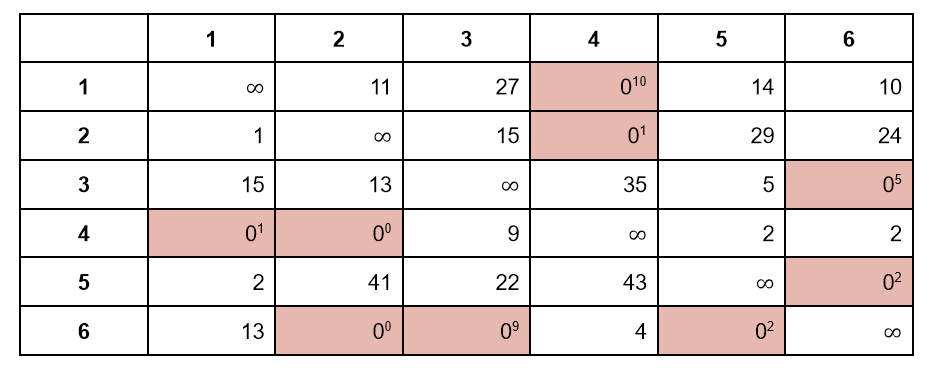
На рисунке цветом выделены все нулевые элементы. Рядом с каждым записан суммарный штраф. Максимальный штраф — он как раз и соответствует ребру :
Исключение ребра
Спускаясь по левому поддереву, мы должны помнить, что ребро
в маршрут включать нельзя. Алгоритм Литтла предлагает хранить ее непосредственно в матрице смежности, поместив особое значение в первую строку четвертого столбца. Как и раньше, мы можем хранить очень большое число или константу Infinity.
Рассмотрим новую матрицу для левого поддерева. Обратите внимание, что она может оказаться нередуцированной, как получилось в нашем случае. Редуцируем ее по первой строке четвертого столбца:
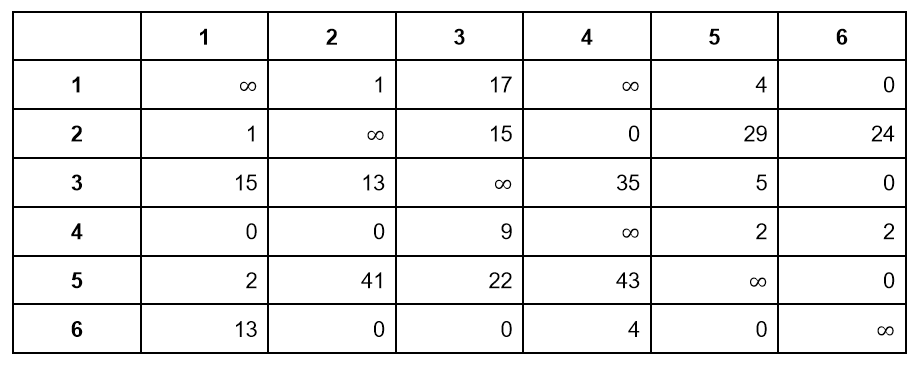
Правое поддерево
Если мы переместились по маршруту , мы больше не можем вернуться в город и уехать в любой другой город. Так происходит, потому что коммивояжер может посетить каждый город только один раз.
Это значит, что выбрав ребро , мы одновременно должны вычеркнуть первую строку четвертого столбца. Другими словами, нужно исключить из матрицы следующие ребра:
Простой способ вычеркнуть строку и столбец — заполнить их значением .
Кроме того, переехав по маршруту мы не можем вернуться. Поэтому ребро также можно исключить, записав в соответствующую ячейку значение .
На рисунке показана матрица после этих преобразований:
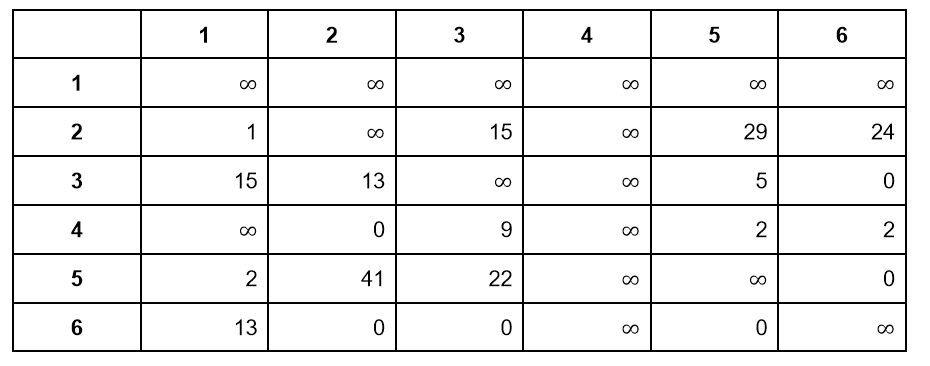
Ее можно редуцировать, вычтя минимумы из каждой строки и каждого столбца:
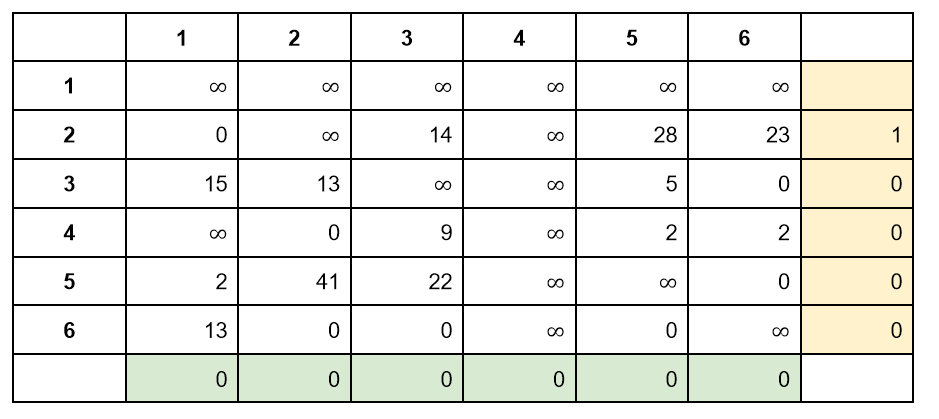
Посчитаем сумму минимумов:
Эту сумму минимумов надо прибавить к предыдущей нижней границе. Так мы получим нижнюю границу правого поддерева :
Цикл
Таким образом, мы построили два поддерева. Пока у нас не хватает информации для отсечения, поэтому мы оставляем оба поддерева и выбираем одно из них для последующего ветвления. Разумно выбирать узел с наименьшей нижней границей. В нашем примере это правый узел, включающий ребро .
Берем матрицу правого поддерева. Она уже редуцирована, так что мы ищем нулевой элемент с максимальным штрафом:
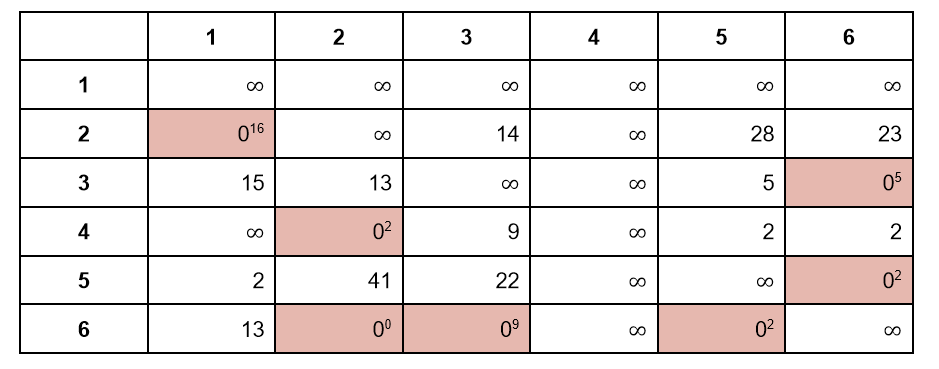
Максимальный штраф — , он соответствует ребру . Его мы и выберем для ветвления дерева. Как и на первом шаге, левое поддерево будет соответствовать маршрутам без ребра . В матрице левого поддерева достаточно записать во вторую строку первого столбца:
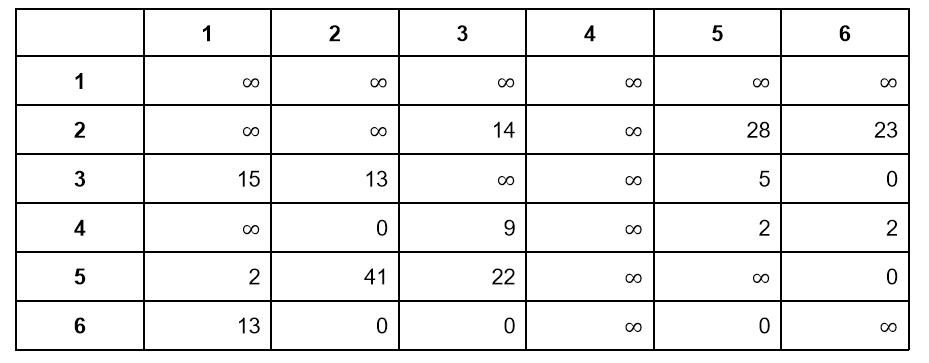
В правом поддереве мы вычеркиваем вторую строку первого столбца — заполняем их значением .
Также нам надо избавиться от обратного ребра . Но оно уже вычеркнуто из матрицы на предыдущем шаге, так что мы ничего дополнительно не делаем:
В алгоритме Литтла маршрут не строится последовательно, как это было в методе перебора. На каждом шаге мы выбираем ребро с максимальным штрафом. Два последовательно выбранных ребра могут даже не соединяться друг с другом.
В нашем примере ребра и соединены через вершину . Добавим к ним ребро и замкнем маршрут — правда, он будет пролегать не по всем шести городам, а только по трем.
Это нарушает условие задачи коммивояжера, поэтому мы должны исключить ребро из матрицы, поместив в ячейку .
Делаем редукцию получившейся матрицы:
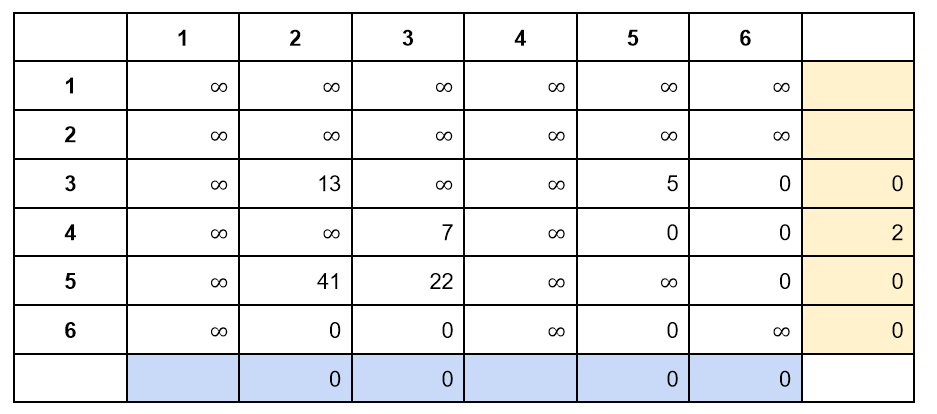
Нижняя граница для правого поддерева увеличивается на:
В итоге новая нижняя граница будет равна :
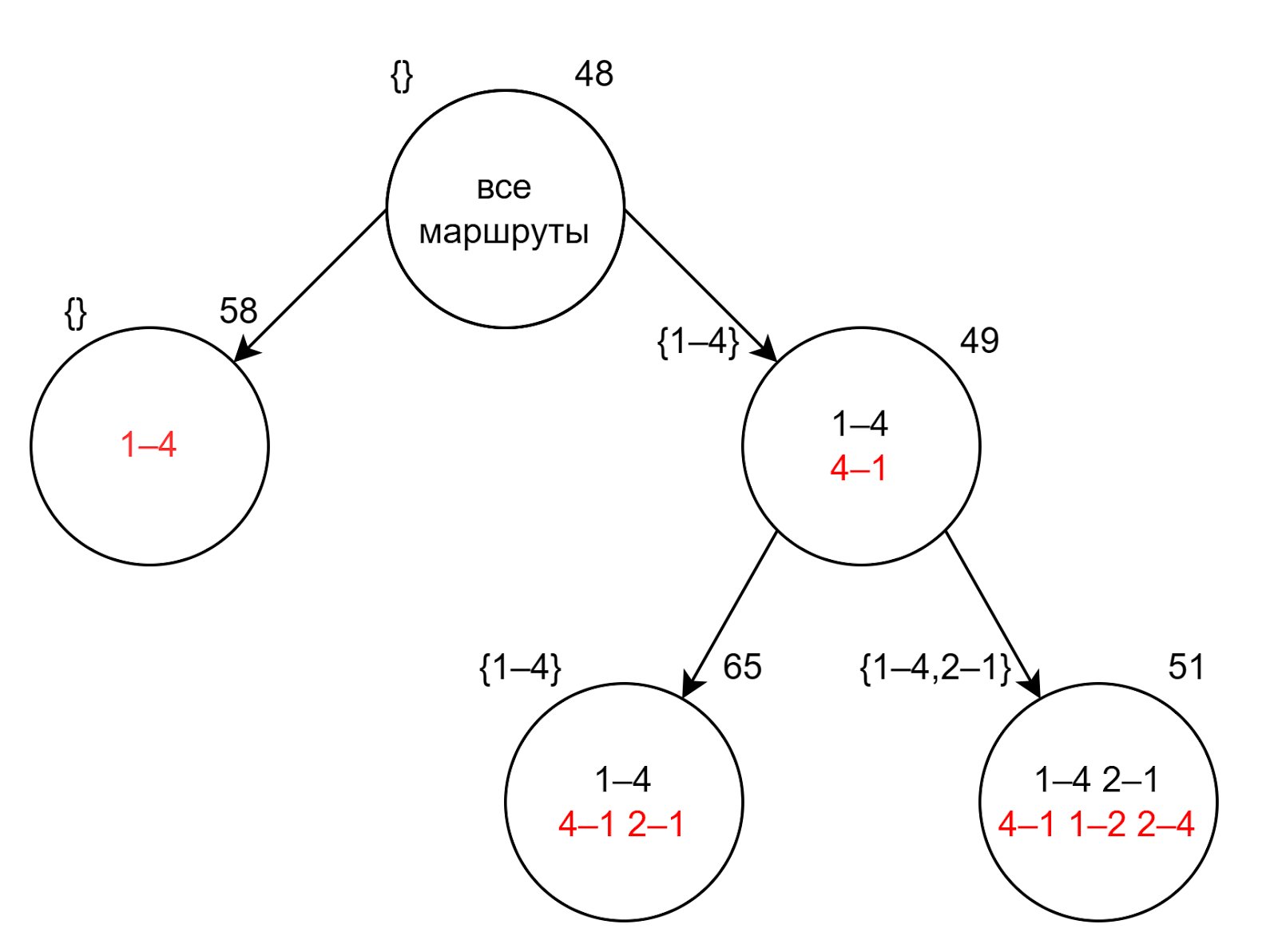
Сейчас у нас есть список вершин, доступных для ветвления. В нем находятся вершины с нижней границей , и . Как и раньше, продолжим ветвление узла с наименьшей оценкой.
Выбираем ребро с наибольшим штрафом :
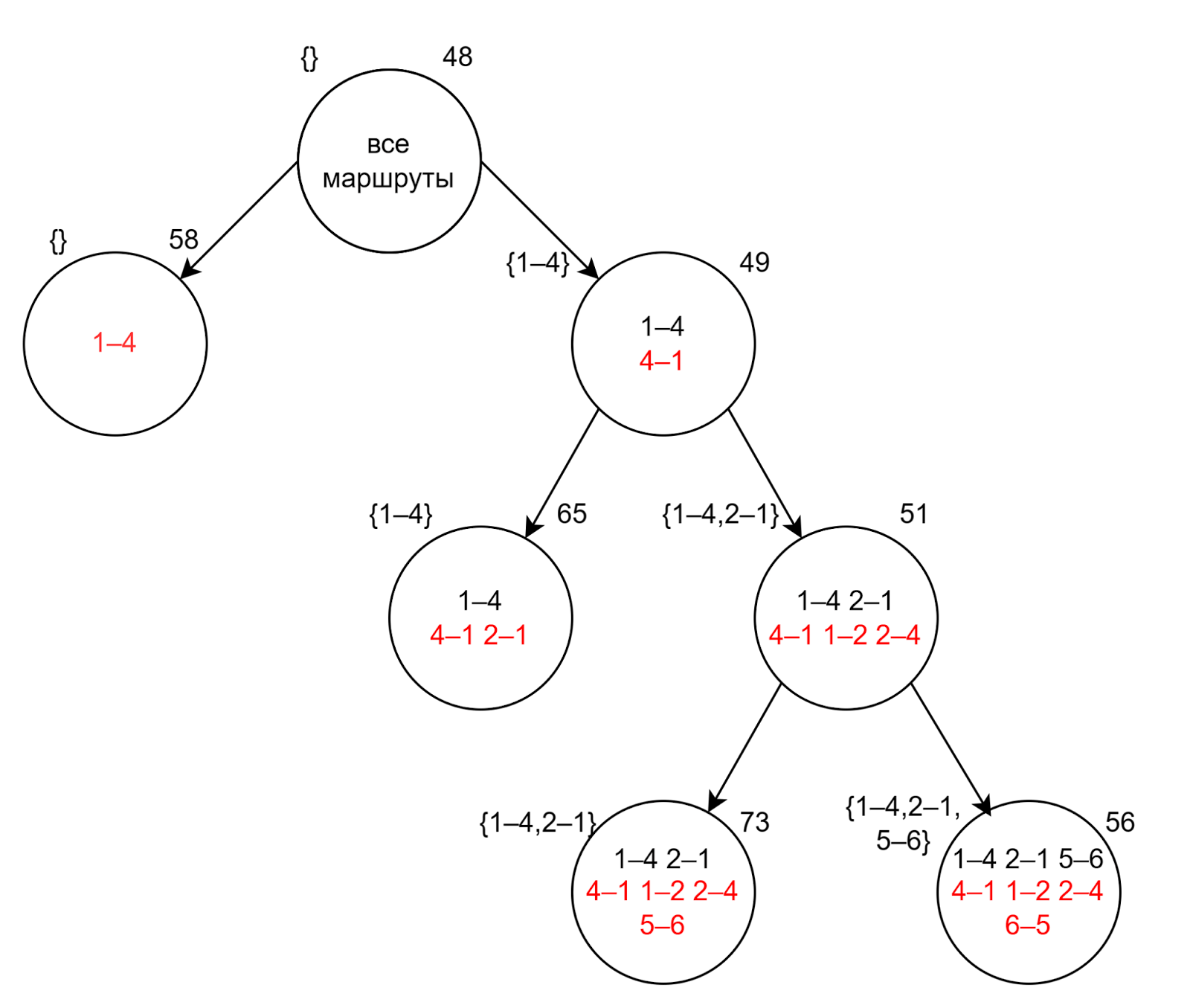
Продолжаем ветвление узла с наименьшей оценкой . Здесь максимальный штраф соответствует ребрам и . Для ветвления мы можем выбрать любое ребро, для примера пусть будет :
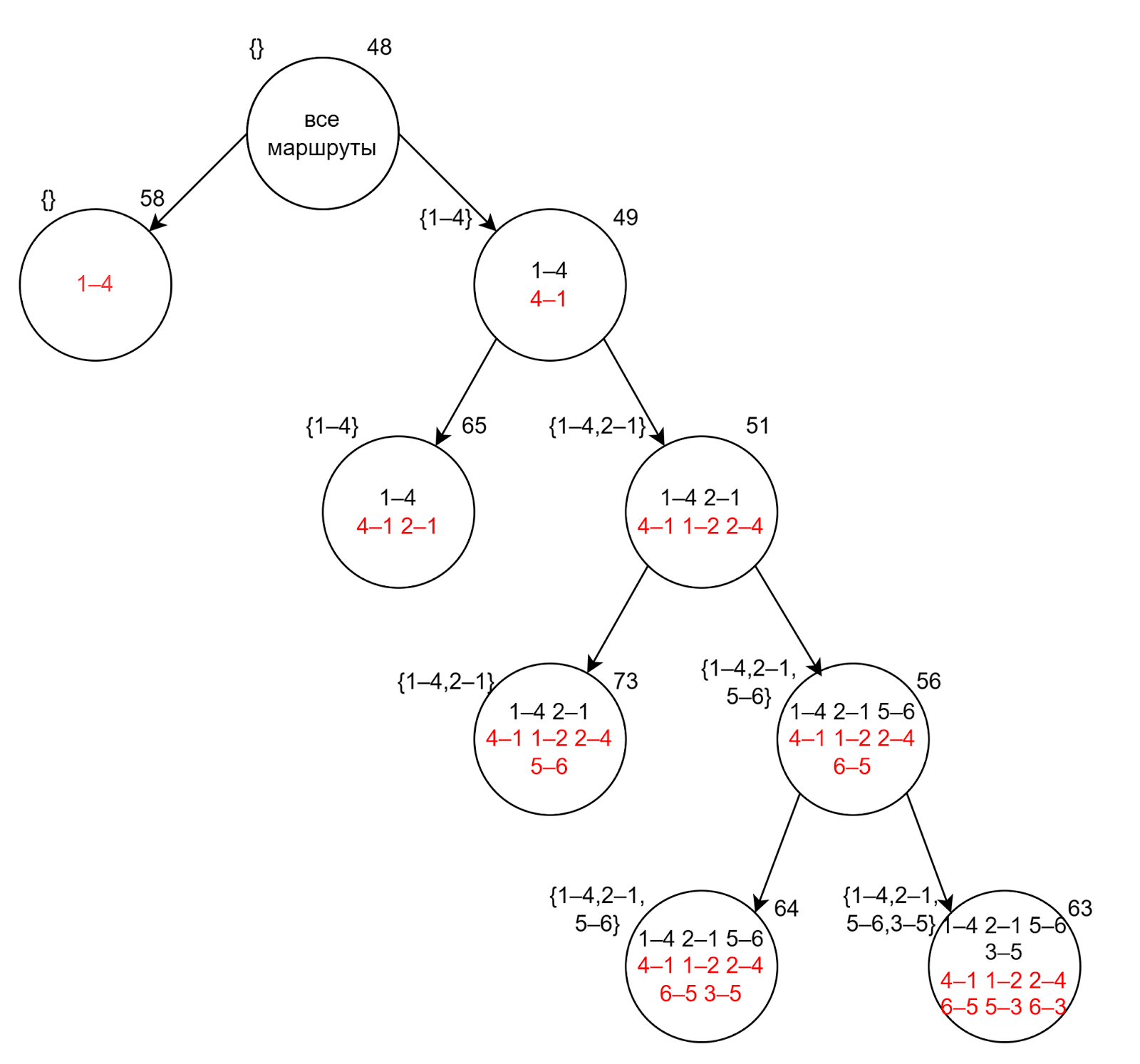
В самом правом поддереве можно образовать короткий маршрут из трех ребер:
Этот короткий цикл не является решением, поэтому вычеркиваем ребро из матрицы.
На этом этапе мы уже привыкли к тому, что продолжаем ветвление самого правого поддерева. Но сейчас нижняя граница длины маршрута в этом поддереве равна , хотя вверху слева у нас есть поддерево с оценкой .
Возвращаемся к узлу, где вычеркнуто ребро . Разбиваем его на два поддерева:
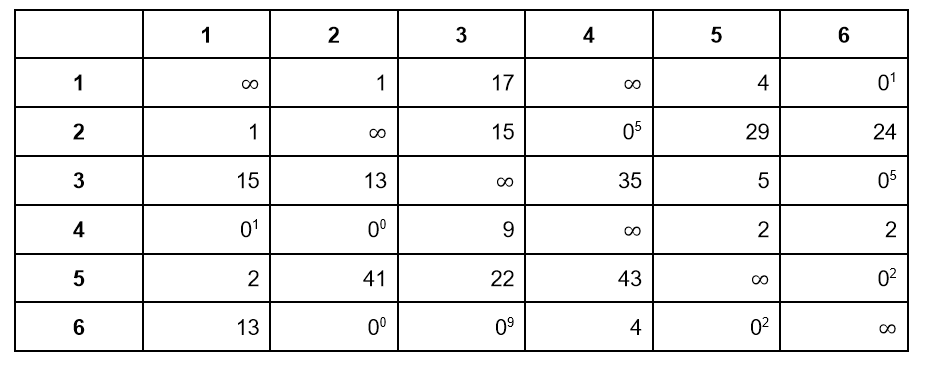
Среди всех ребер есть с максимальным штрафом — . Таким образом:
-
Стоимость левого поддерева равна , если вычеркнуть ребро
-
Стоимость правого поддерева равна , если вычеркнуть ячейку и шестую строку третьего столбца
На схеме это выглядит так:
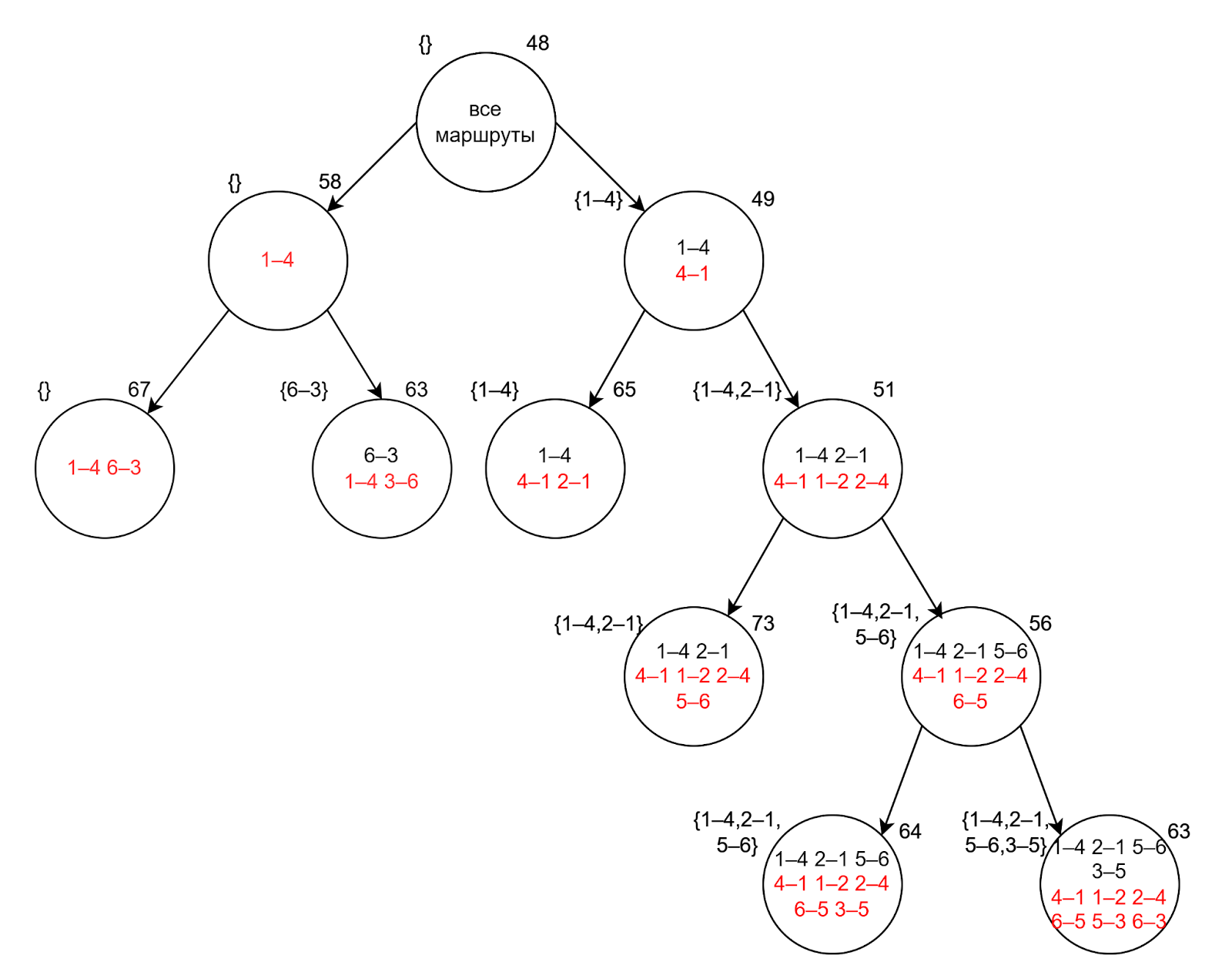
На этом этапе мы ни разу не проводили отсечение, потому что пока у нас нет ни одного построенного маршрута.
Сейчас в дереве решений есть два узла с минимальной нижней границей . Мы можем выбрать любое из них. Выберем самое правое поддерево и посмотрим на его матрицу:
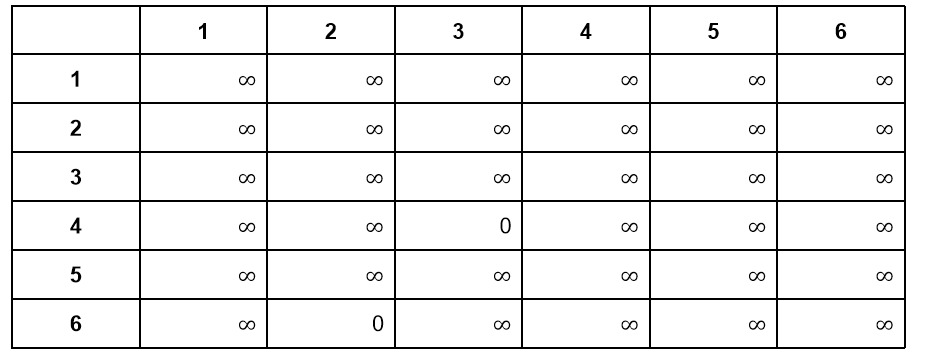
В этот момент мы останавливаемся, потому что у нас останется только два решения — два значения в матрице, которые меньше .
Фактически, сейчас у нас нет выбора — нам нужно найти два недостающие ребра и вставить их в маршрут в произвольном порядке. В нашем случае это ребра и . Если бы в ячейках были ненулевые значения, то нам бы потребовалась редукция — в данном случае она не нужна.
Нижняя граница длины маршрута в поддереве равна единственному маршруту в нем — а именно :
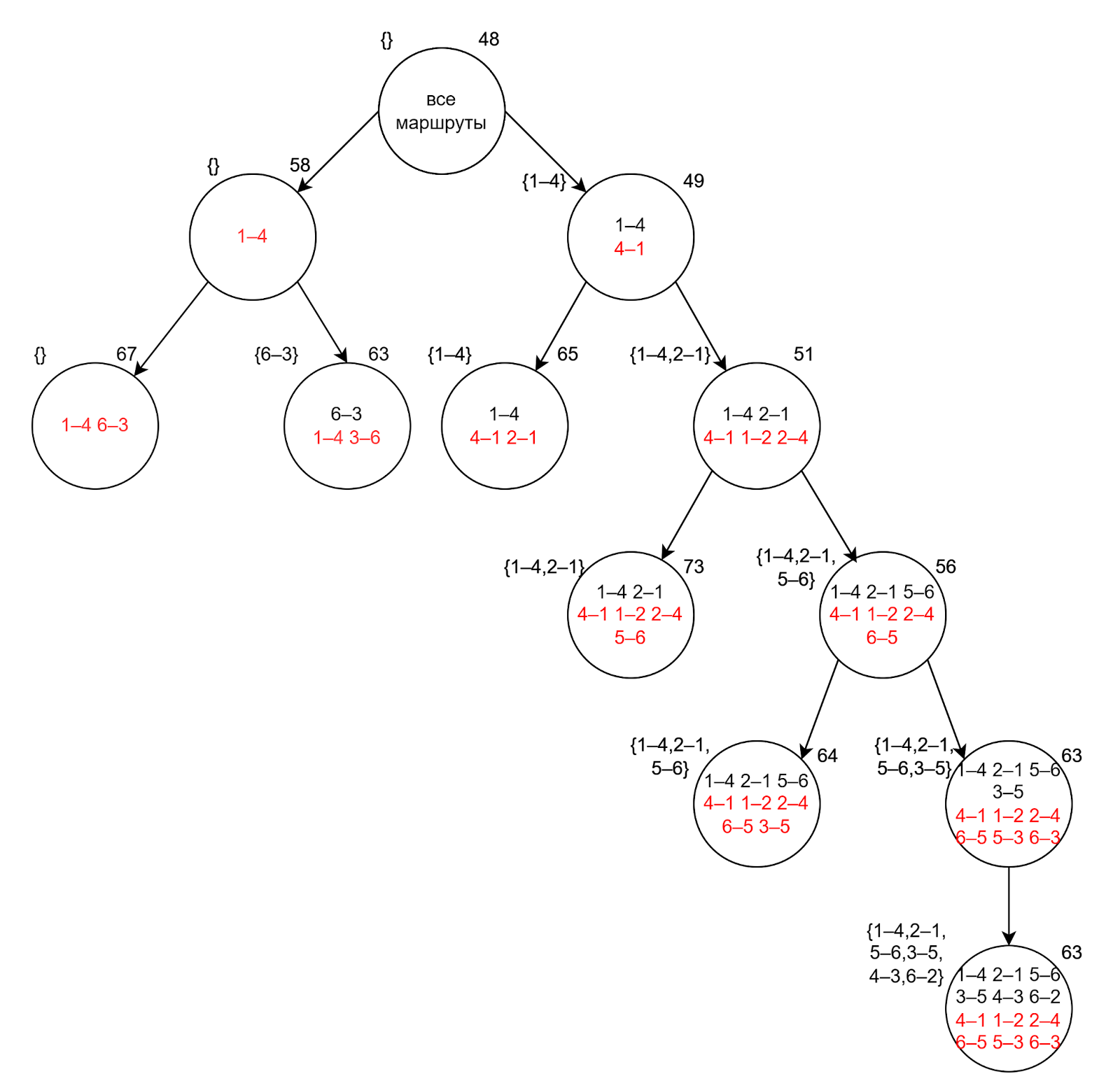
Итак, мы построили первый маршрут длиной . У нас есть недостроенные поддеревья с нижними границами и . Нет ни одного поддерева с нижней границей меньше . Это значит, что в дереве решений точно нет маршрута, который мы уже нашли. Работу алгоритма можно завершить.
Если бы у нас оказалось несколько узлов с меньшей нижней границей, мы бы оставили только их, а остальные бы отсекли.
Самый короткий маршрут из найденных называется рекордным маршрутом или рекордом. На каждом шаге алгоритма мы можем отсекать поддеревья с нижней границей, которая больше или равна длине рекордного маршрута.
Мы последовательно достраиваем очередное поддерево до конца и получаем новый маршрут. При этом мы должны постоянно проверять, не короче ли новый маршрут текущего рекорда. Если короче, он сам должен стать новым рекордным маршрутом.
Выводы
В этом уроке мы познакомились с алгоритмом Литтла. Повторим ключевые выводы:
-
Алгоритм Литтла находит оптимальное решение в дереве решений
-
Для работы алгоритма важно, чтобы оценка нижней границы была корректной
-
Обычно алгоритм Литтла работает быстрее метода перебора, в худшем случае — с той же скоростью
Пока наше знакомство ограничилось только теорией, но уже в следующем уроке мы разберем, как реализовать алгоритм Литтла на практике.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
- Статья «Как учиться и справляться с негативными мыслями»
- Статья «Ловушки обучения»
- Статья «Сложные простые задачи по программированию»
- Вебинар «Как самостоятельно учиться»
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
