Древовидные структуры достаточно гибкие по своей задумке. Один и тот же набор значений можно расположить в виде дерева, если использовать разные топологические решения. В итоге два дерева с одинаковым содержимым будут обладать противоположными характеристиками, например, по скорости поиска узлов.
Ученые еще в середине прошлого века заинтересовались вопросом оптимизации хранения данных в деревьях. Они хотели обеспечить максимальную скорость поиска в них. Так появились сбалансированные деревья.
В этом уроке мы детально познакомимся с балансировкой деревьев, способами ребалансировки при добавлении новых узлов, а также рассмотрим новые виды древовидных структур.
Сбалансированные деревья
Идеальная сбалансированность — это свойство дерева, при котором все его уровни, иногда кроме последнего, полностью заполнены.
Для сравнения рассмотрим два бинарных дерева поиска, которые будут представлять собой одну последовательность элементов — 1,2,3,4,5,6. Из этой последовательности можно построить несколько деревьев, например:
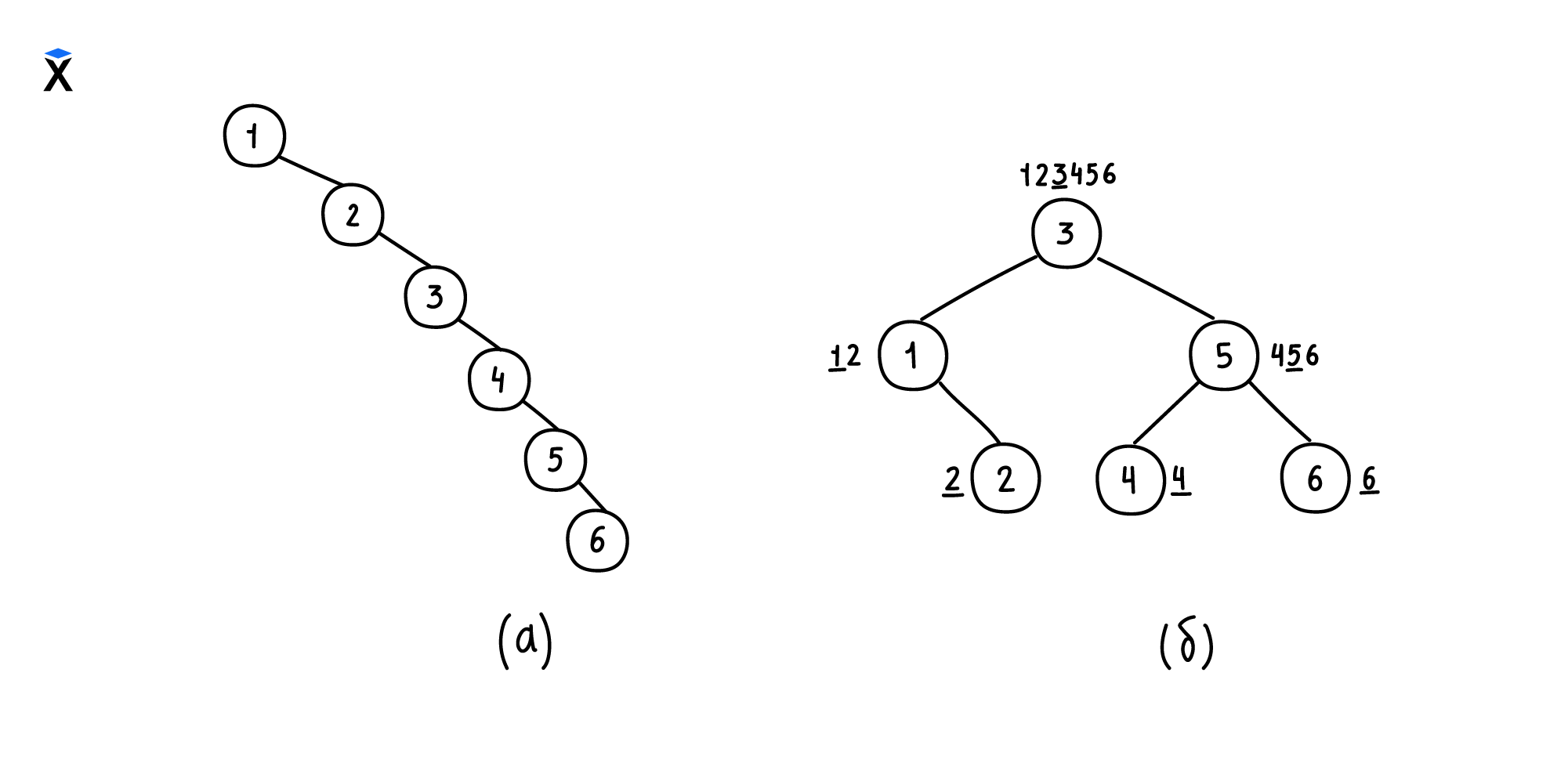
В дереве (б) каждый из уровней, кроме левой ветки узла 1, заполнены. Значит, дерево (б) — идеально сбалансированное дерево. Что нельзя сказать о дереве (а).
Дерево (а) и дерево (б) можно отнести к бинарным деревьям поиска. Но для худшего случая — поиска в дереве элемента №6 в дереве (а) — требуется выполнить шесть операций перехода между вершинами, а в случае (б) — только три.
Дерево с максимально возможной высотой (а) называется разбалансированным или вырожденным деревом. Оно не отличается от двусвязного списка, значит, теряет свое основное преимущество — скорость поиска.
Для разбалансированных деревьев скорость составляет . А для идеально сбалансированного дерева (б) поиск будет завершен за число шагов, которые не превышают высоту дерева или за .
Состояние идеальной сбалансированности в дереве трудно поддерживать. Любое добавление или удаление узла в сбалансированном дереве может привести к ситуации, когда дерево выйдет из идеально сбалансированного состояния. В таком случае скорость поиска будет значительно деградировать после каждой вставки или удаления узла.
Чтобы вернуть дерево в сбалансированный вид, его перестраивают после каждой манипуляции с составом узлов. Рассмотрим пример с добавлением элемента №7 в наше дерево. Это можно сделать несколькими способами:
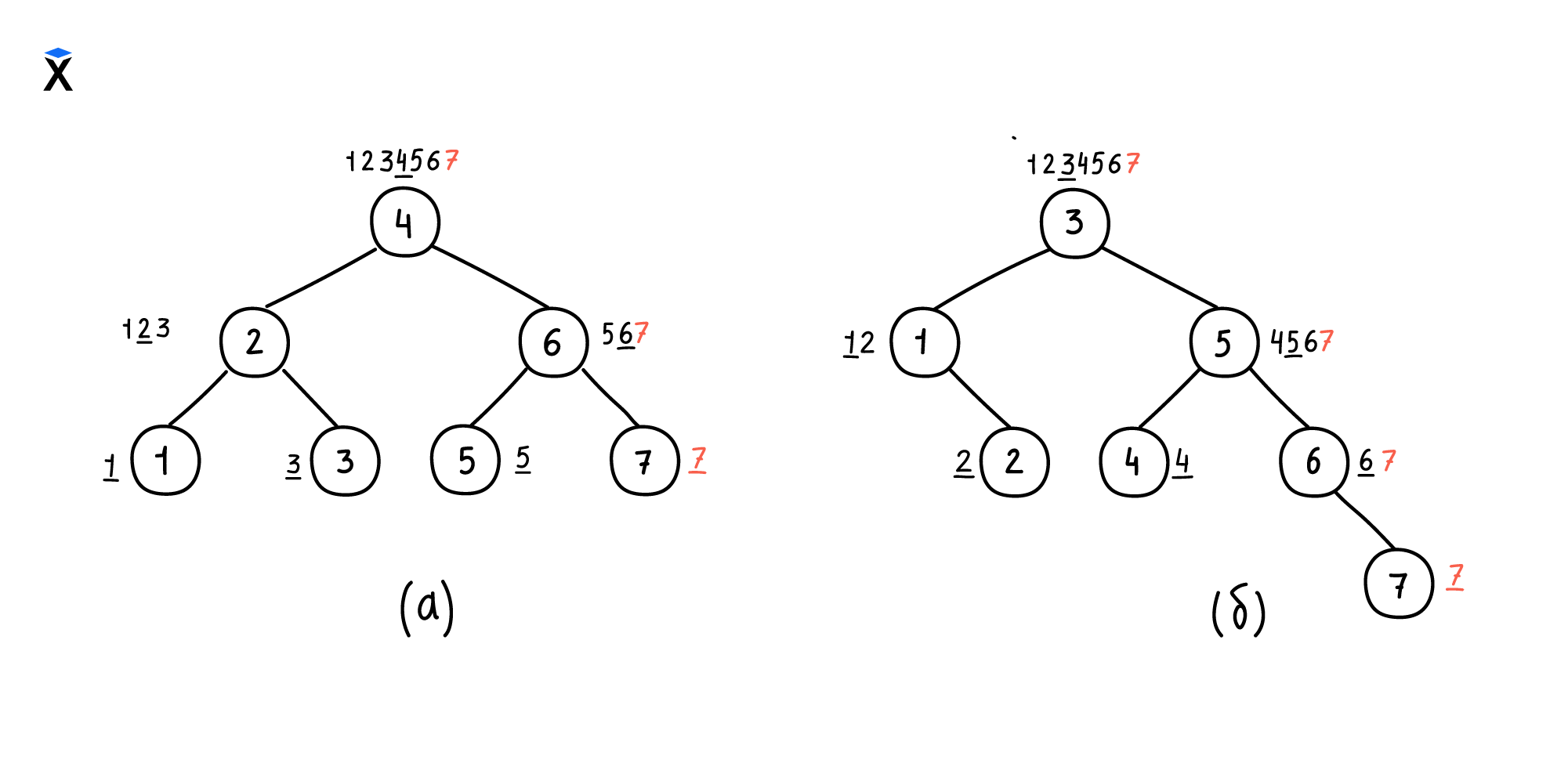
В случае (б) дерево вышло из состояния идеальной сбалансированности, так как оба нижних уровня не заполнены полностью. В таком случае поиск элемента №7 будет выполнен за четыре операции.
В случае (а) элементы были перераспределены, чтобы сохранить сбалансированное состояние. В таком случае поиск элемента №7 будет выполнен всего за три операции.
На таких маленьких примерах выигрыш в одну операцию во время поиска может показаться слишком незначительным, чтобы постоянно перестраивать дерево. Но при работе с деревьями из миллионов узлов и повышенных требованиях к скорости выборки такое перестроение может себя оправдать. Пользователям очень нравится, когда приложение работает со скоростью человеческой мысли.
Ресурсы вычислительных машин не безграничны. Чтобы снизить нагрузку на них и одновременно с этим максимально сохранить преимущества идеально сбалансированного дерева, придумали новые виды деревьев. Среди них особенно выделяются АВЛ-деревья и красно-черные деревья, с которыми мы познакомимся подробнее.
АВЛ-деревья
Этот вид деревьев представили в 1962 году двое советских ученых: Адельсон-Вельский Г.М. и Ландис Е.М. Именно по сокращению от их фамилий АВЛ-деревья и получили такое название.
АВЛ-деревья отличаются от идеально сбалансированных. АВЛ-дерево считается сбалансированным, если для каждого узла дерева высота его правого и левого поддеревьев отличаются не более чем на единицу. Если модификация структуры узлов приводит к нарушению сбалансированности дерева, то необходимо выполнить его балансировку.
Поиск в АВЛ-дереве выполняется аналогично работе с бинарным деревом поиска. При этом благодаря поддержке возможности ребалансировки при вставки и удалении узлов в АВЛ-деревьях есть особенности реализации.
В качестве индикатора наличия разбалансированности в поддереве на узел выносят показатель баланса, который принимает значения от -1 до +1. Их значения:
-
–1 — в правом поддереве больше высота
-
0 — поддеревья равной высоты
-
+1 — высота больше в левом поддереве
В итоге код нашего узла принимает следующий вид:
class AvlTreeNode {
constructor(value, parent) {
this.left = null; //ссылка на левый дочерний узел
this.right = null; //ссылка на правый дочерний
this.balanceFactor = 0; //показатель сбалансированности
this.parent = parent; //ссылка на родителя
this.value = value; //полезная нагрузка
}
}Java
class AvlTreeNode {
public AvlTreeNode left = null; // ссылка на левый дочерний узел
public AvlTreeNode right = null; // ссылка на правый дочерний
public int balanceFactor = 0; // показатель сбалансированности
public AvlTreeNode parent; // ссылка на родителя
public Object value; // полезная нагрузка
AvlTreeNode(Object value, AvlTreeNode parent) {
this.parent = parent;
this.value = value;
}
}Python
class AvlTreeNode:
def __init__(self, value, parent=None):
self.left = None # ссылка на левый дочерний узел
self.right = None # ссылка на правый дочерний узел
self.balance_factor = 0 # показатель сбалансированности
self.parent = parent # ссылка на родителя
self.value = value # полезная нагрузкаPHP
<?php
class AvlTreeNode
{
public $left = null; // ссылка на левый дочерний узел
public $right = null; // ссылка на правый дочерний
public $balanceFactor = 0; // показатель сбалансированности
public $parent; // ссылка на родителя
public $value; // полезная нагрузка
public function __construct($value, $parent)
{
$this->parent = $parent;
$this->value = $value;
}
}Этот фрагмент кода определяет базовый скелет узла нашего будущего дерева. Чтобы превратить его в полноценное АВЛ-дерево, нужно добавить возможность искать и модифицировать узлы. Операцию поиска можно переиспользовать из бинарных деревьев поиска, а изменение в структуре дерева потребует дополнительной частичной ребалансировки.
Далее мы подробно поговорим об операциях добавления и удаления узлов в АВЛ-деревьях.
Модификация структуры узлов
Добавить новую вершину можно с помощью рекурсивного спуска к месту вставки нового узла. Если возвращаться к корневой вершине через каждый промежуточный узел, то добавивший новую вершину метод модифицирует значение balanceFactor. Если новое значение выходит из допустимого диапазона, то выполняется ребалансировка данного поддерева.
Ребалансировка деревьев осуществляется при помощи специальных механизмов — методов вращения. Вращения бывают двух видов: левое и правое.
Вращение вправо выполняется за три шага:
-
Текущий корень поддерева (D) заменяется на левый дочерний узел (B)
-
Предыдущий корень (D) становится правым дочерним узлом для (B)
-
Предыдущее правое поддерево узла (B) становится левым поддеревом для (D)
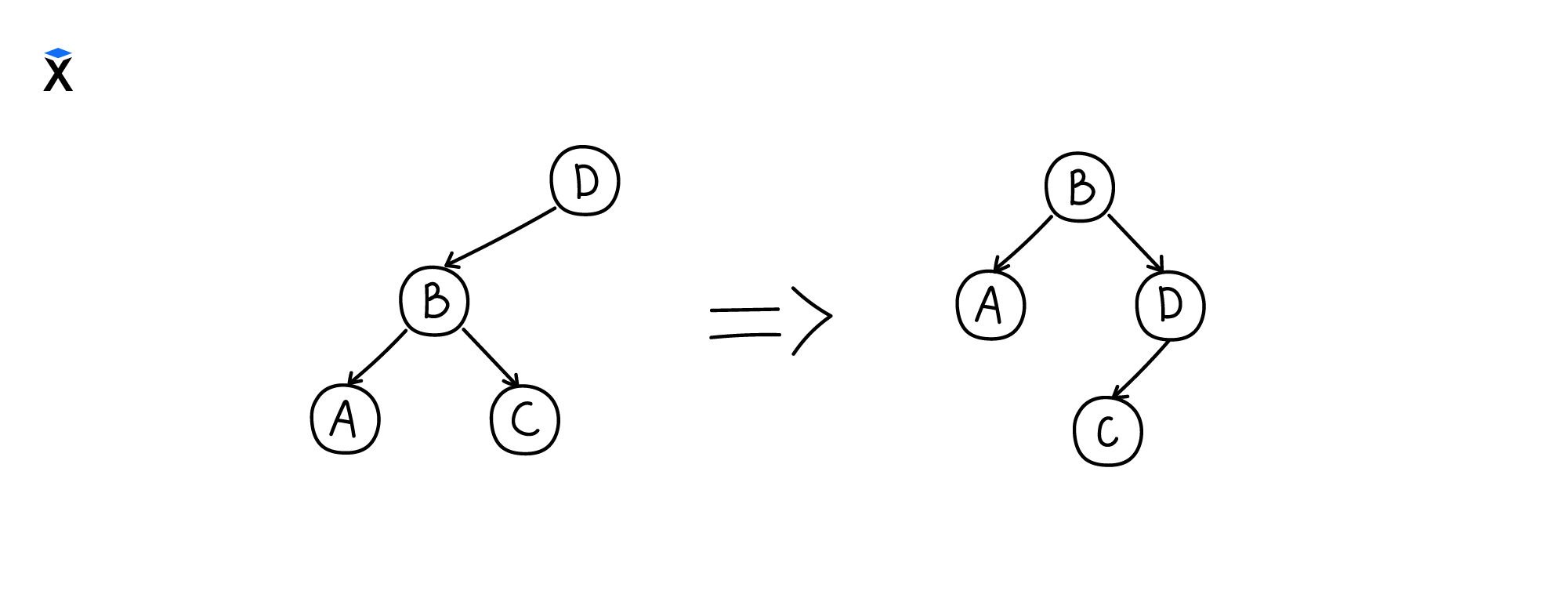
Вращение влево выполняется аналогично:
-
Текущий корень поддерева (D) заменяется на правый дочерний узел ©
-
Предыдущий корень (D) становится левым дочерним узлом для ©
-
Предыдущее левое поддерево узла © становится правым поддеревом для (D)
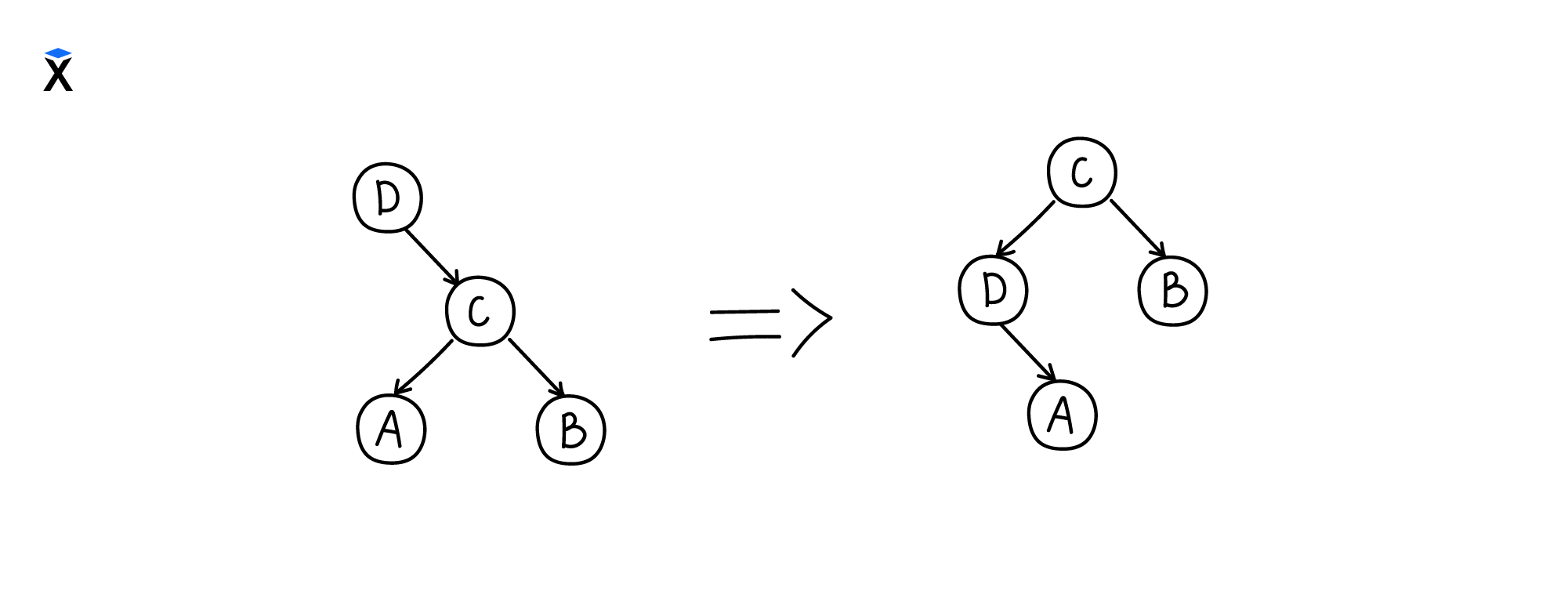
В зависимости от того, куда добавили новую вершину, возможны различные комбинации выполнения вращений. Они помогут вернуть дерево в сбалансированное состояние.
Всего выделяется четыре варианта развития событий:
-
Левое поддерево левой дочерней вершины
-
Левое поддерево правой дочерней вершины
-
Правое поддерево левой дочерней вершины
-
Правое поддерево правой дочерней вершины
Рассмотрим пример, который описывает первый случай — вставку в левое поддерево левой дочерней вершины. Изображенные треугольники представляют собой сбалансированные АВЛ-поддеревья. Они могут содержать большое количество вершин. У вершины В дерево не сбалансировано, поскольку поддерево А1 в вершине А на два уровня выше, чем поддерево В2:
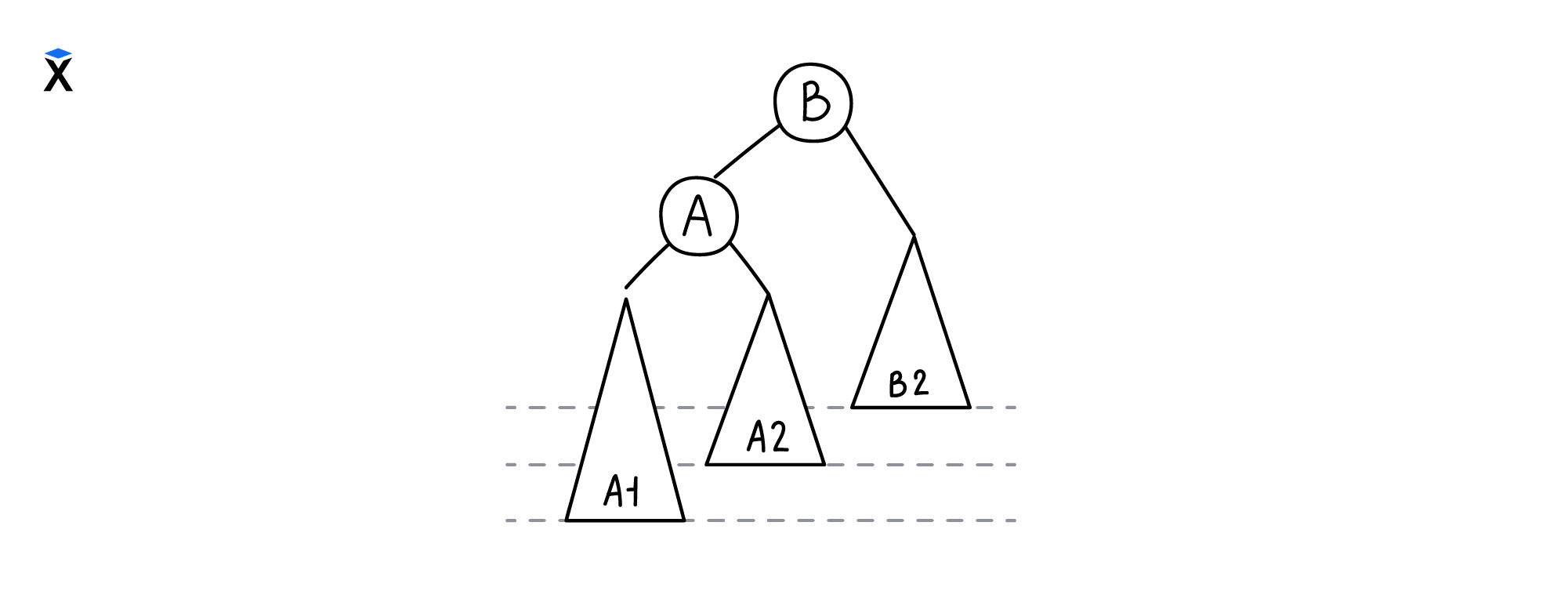
Чтобы сбалансировать дерево, необходимо совершить правое вращение — заменить вершину В вершиной А и сделать поддерево А2 левым поддеревом вершины В. После такого преобразования наше поддерево примет следующий вид:
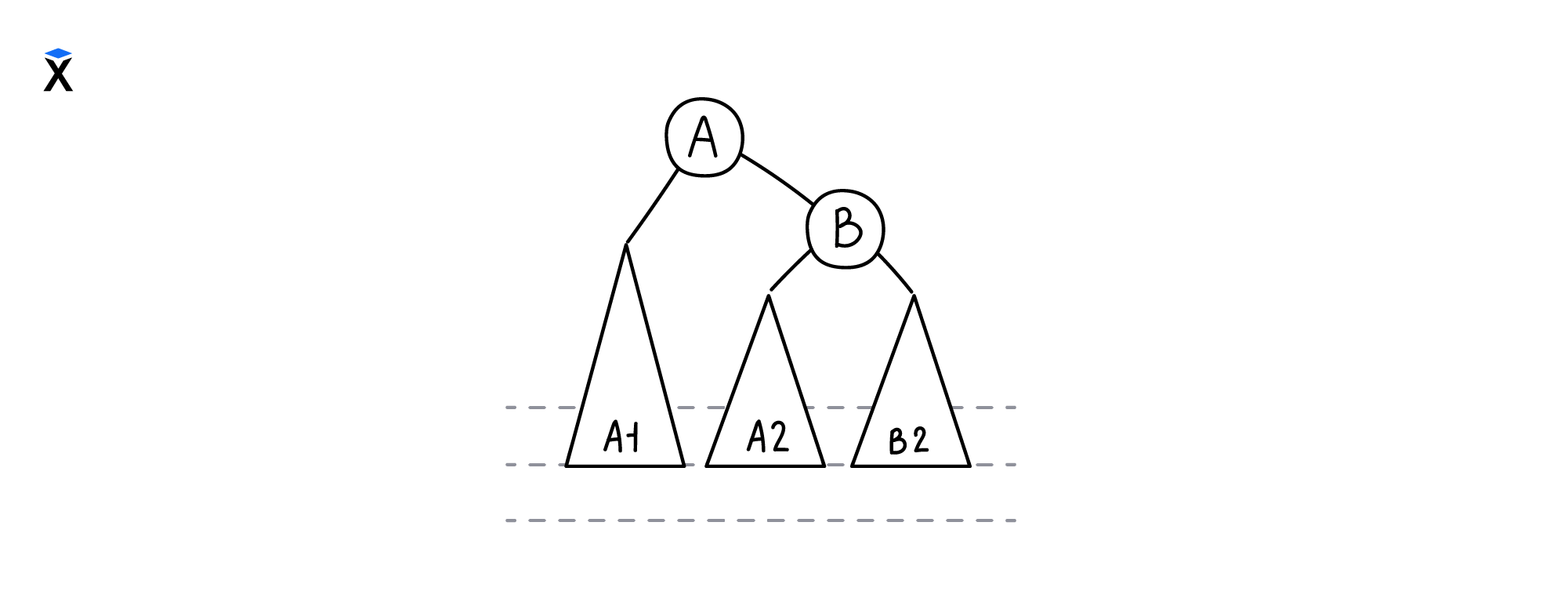
Четвертый сценарий будет выглядеть аналогично кроме замены способа вращения на левое.
Для второго и третьего сценариев необходимо выполнить вращение дважды:
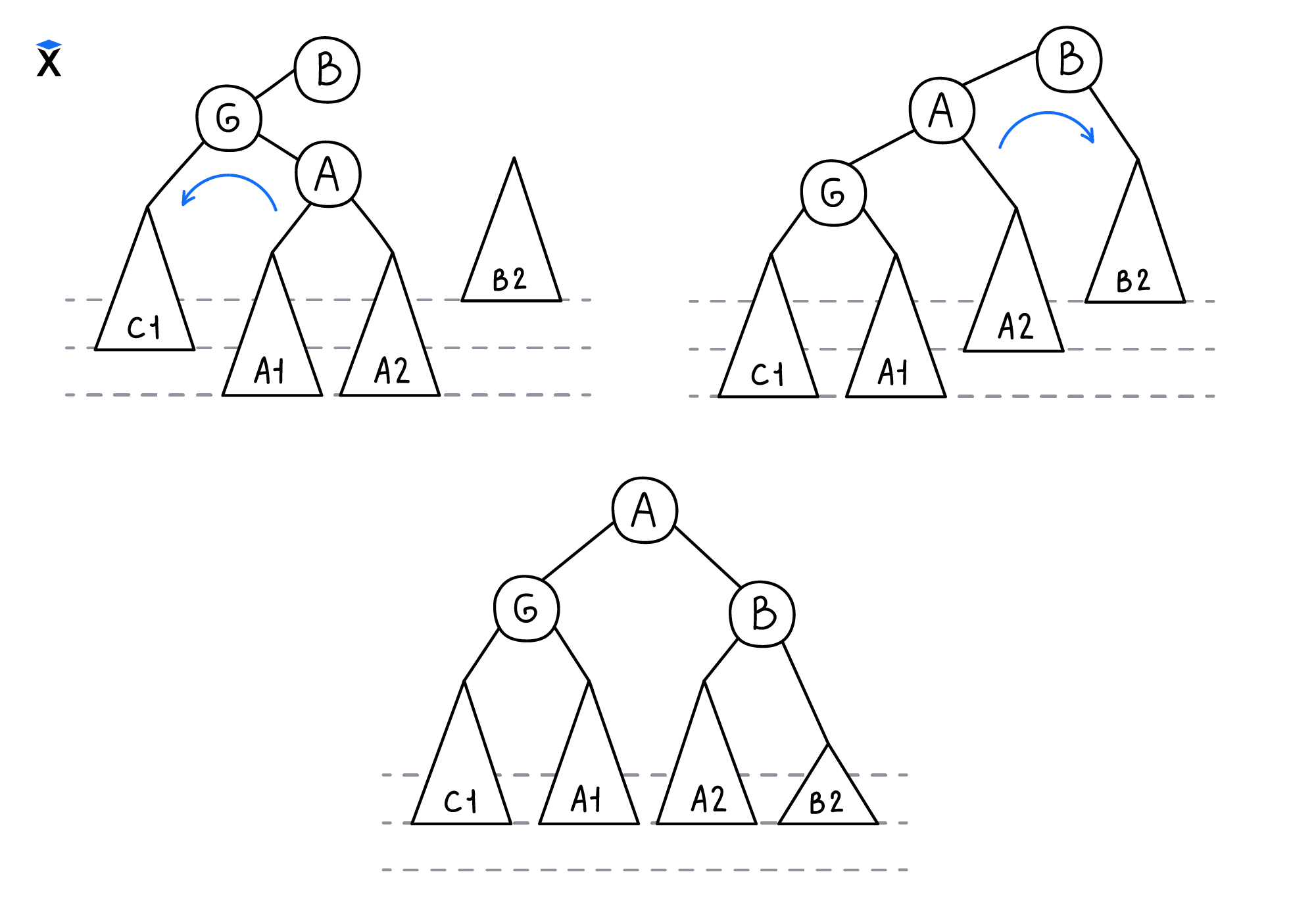
Удаление узлов также осуществляется при помощи механизмов вращения. При возврате во время рекурсивного спуска осуществляется вычисление balanceFactor. Если он отклоняется от допустимых значений, то выполняется ребалансировка аналогично добавлению узла.
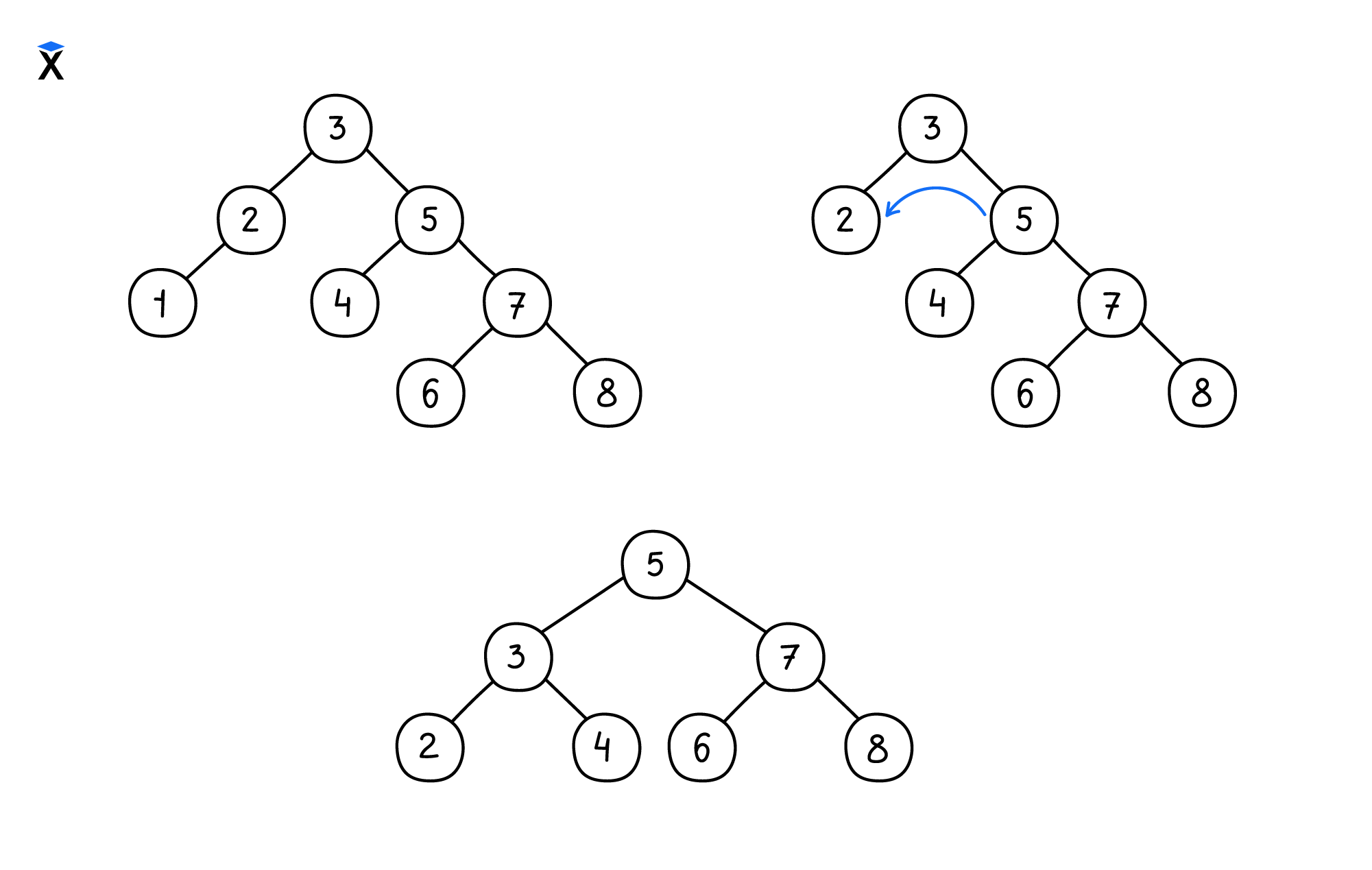
Другим видом автоматически балансирующихся деревьев являются красно-черные деревья, с которыми мы познакомимся дальше.
Красно-черные деревья
Красно-черные деревья — одни из наиболее активно используемых на практике самобалансирующихся деревьев. Они так называются из-за наличия на узле дополнительного поля, в котором размещается цвет узла. В качестве стандартных цветов используют обычно красные и черные узлы, а сам цвет узла используется во время балансировки.
Так как красно-черные деревья самобалансирующиеся, то среднее и худшее время поиска тоже составляют . А операции вставки и удаления узла могут потребовать поворот поддерева.
Для красно-черного дерева наш код узла примет следующий вид:
class RBTreeNode {
constructor(value, parent) {
this.left = null; //ссылка на левый дочерний узел
this.right = null; //ссылка на правый дочерний
this.isRed = false; //цвет узла. Если не красный, то считаем что узел черный
this.parent = parent; //ссылка на родителя
this.value = value; //полезная нагрузка
}
}Java
class RBTreeNode {
public RBTreeNode left = null; // ссылка на левый дочерний узел
public RBTreeNode right = null; // ссылка на правый дочерний
public boolean isRed = false; // Цвет узла
// Если узел не красный, то считаем что он черный
public RBTreeNode parent; // ссылка на родителя
public Object value; // полезная нагрузка
RBTreeNode(Object value, RBTreeNode parent) {
this.parent = parent;
this.value = value;
}
}Python
class RBTreeNode:
def __init__(self, value, parent=None):
self.left = None # ссылка на левый дочерний узел
self.right = None # ссылка на правый дочерний узел
self.is_red = False # цвет узла. Если не красный, то считаем что узел черный
self.parent = parent # ссылка на родителя
self.value = value # полезная нагрузкаPHP
<?php
class RBTreeNode
{
public $left = null; // ссылка на левый дочерний узел
public $right = null; // ссылка на правый дочерний
public $isRed = false; // Цвет узла
// Если узел не красный, то считаем что он черный
public $parent; // ссылка на родителя
public $value; // полезная нагрузка
public function __construct($value, $parent)
{
$this->parent = $parent;
$this->value = $value;
}
}В отличие от других видов деревьев в листовых узлах красно-черных деревьев не хранят полезную нагрузку. А цвет листовых узлов без данных всегда считается черным. Такая особенность позволяет считать ссылку на null валидным узлом. Эта особенность позволит сэкономить память. А само дерево принимает следующий вид:
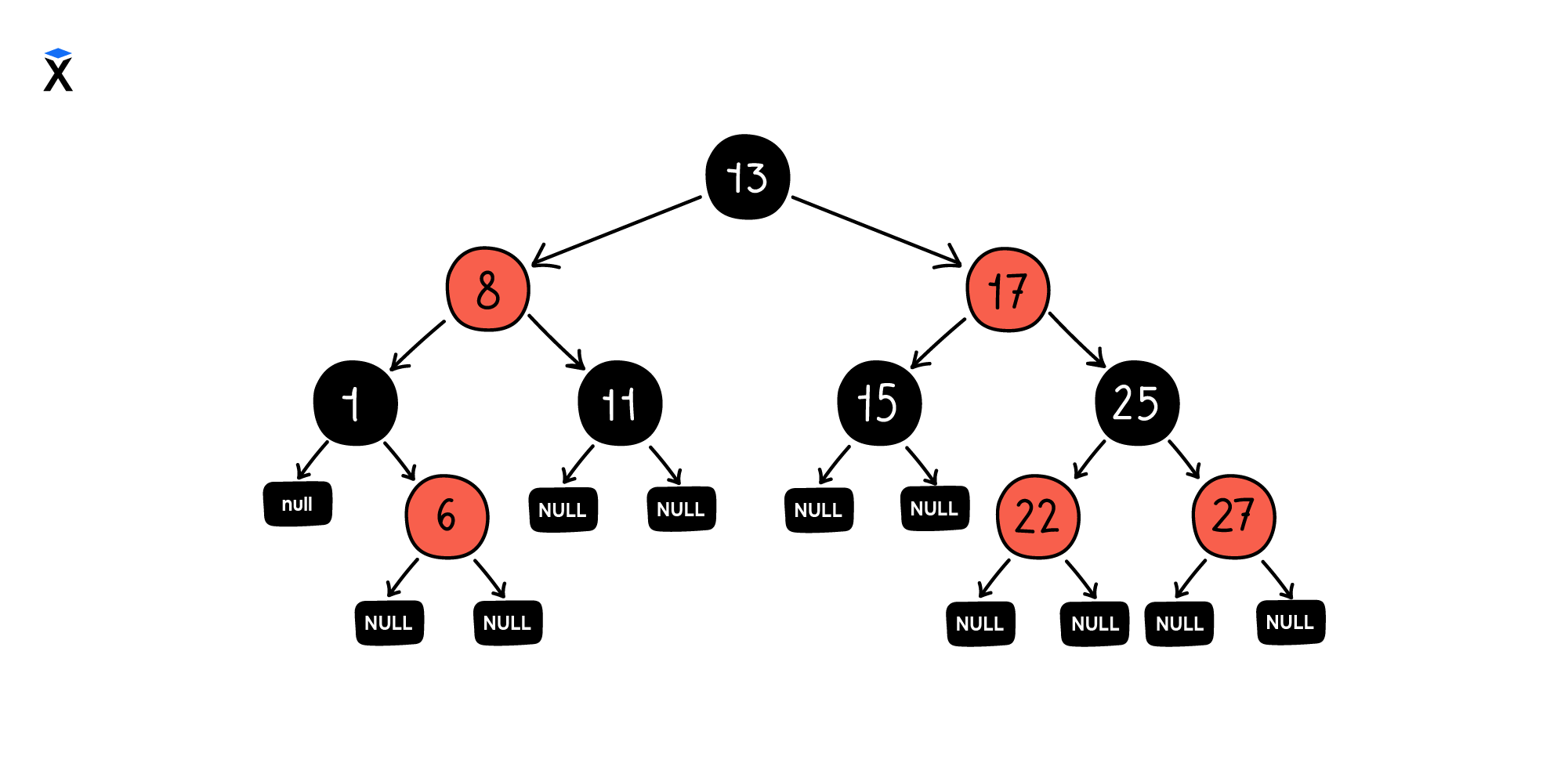
Помимо особенностей работы с листовыми узлами к свойствам красно-черного так же относят:
-
Корень красно-черного дерева черный
-
Две красные вершины не могут идти подряд ни на одном пути. Оба потомка каждого красного узла — черные
-
Для каждой вершины, в каждом исходящем из нее пути, одинаковое число черных вершин
Иногда при работе с узлами красно-черного дерева используют черную высоту — количество черных вершин на исходящих из нее путях, не включая саму исходную вершину.
Чтобы вставить узел, мы сначала ищем в дереве место, куда его следует добавить. Новый узел всегда добавляется как лист, поэтому оба его потомка являются пустыми узлами и предполагаются черными. После вставки красим узел в красный цвет. Далее смотрим на предка и проверяем, не нарушается ли свойства дерева, которые описали выше. Если необходимо, мы перекрашиваем узел и производим поворот, чтобы сбалансировать дерево.
Сбалансированность этих деревьев хуже, чем у АВЛ-деревьев. При этом затраты на поддержание состояния сбалансированности и потребление памяти меньше, а операцию поиска можно выполнять одновременно с выполнением перестроения дерева.
Благодаря этим преимуществам сфера применения красно-черных деревьев существенно шире. Так, например, в стандартной библиотеке шаблонов языка C++ STL и TreeMap в Java применяются именно красно-черные деревья.
Выводы
Хранение данных в идеально сбалансированных деревьях позволяет достичь скорости поиска . Но чтобы поддерживать идеальную сбалансированность, требуются существенные ресурсные затраты на полное перестроение дерева при добавлении нового элемента.
Чтобы решить эту проблему, были придуманы новые виды деревьев: АВЛ-деревья и красно-черные деревья. Использование таких подходов поможет сохранить преимущества бинарных деревьев поиска и не тратить большое количество ресурсов. Так можно поддерживать идеальную согласованность.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
