Алгоритмы на деревьях

Теория: Бинарные деревья

Полный доступ к материалам

Зарегистрируйтесь и получите доступ к этому и десяткам других курсов

Организация хранения данных в виде дерева позволяет обойти ограничения линейной структуры данных. Например, в последней нельзя организовать быстрыми поиск и вставку элементов одновременно. При этом в иерархической структуре данных можно эффективно выбирать и обновлять большие объемы данных.

Один из наиболее часто используемых и простых в реализации подвидов деревьев — бинарные деревья. Помимо организации поиска, бинарные деревья используют, когда разбирают математические выражения и компьютерные программы. Еще их используют, чтобы хранить данные для алгоритмов сжатия, а также они лежат в основе других структур данных, например, очереди с приоритетом, кучи и словари.

В этом уроке мы познакомимся с устройством и особенностями бинарных деревьев и разберем основные операции с его узлами.

Что такое бинарные деревья

Бинарное дерево или двоичное дерево — это дерево, в котором у каждого из его узлов не более двух дочерних узлов. При этом каждый дочерний узел тоже представляет собой бинарное дерево.

Рассмотрим примеры деревьев на следующем рисунке:

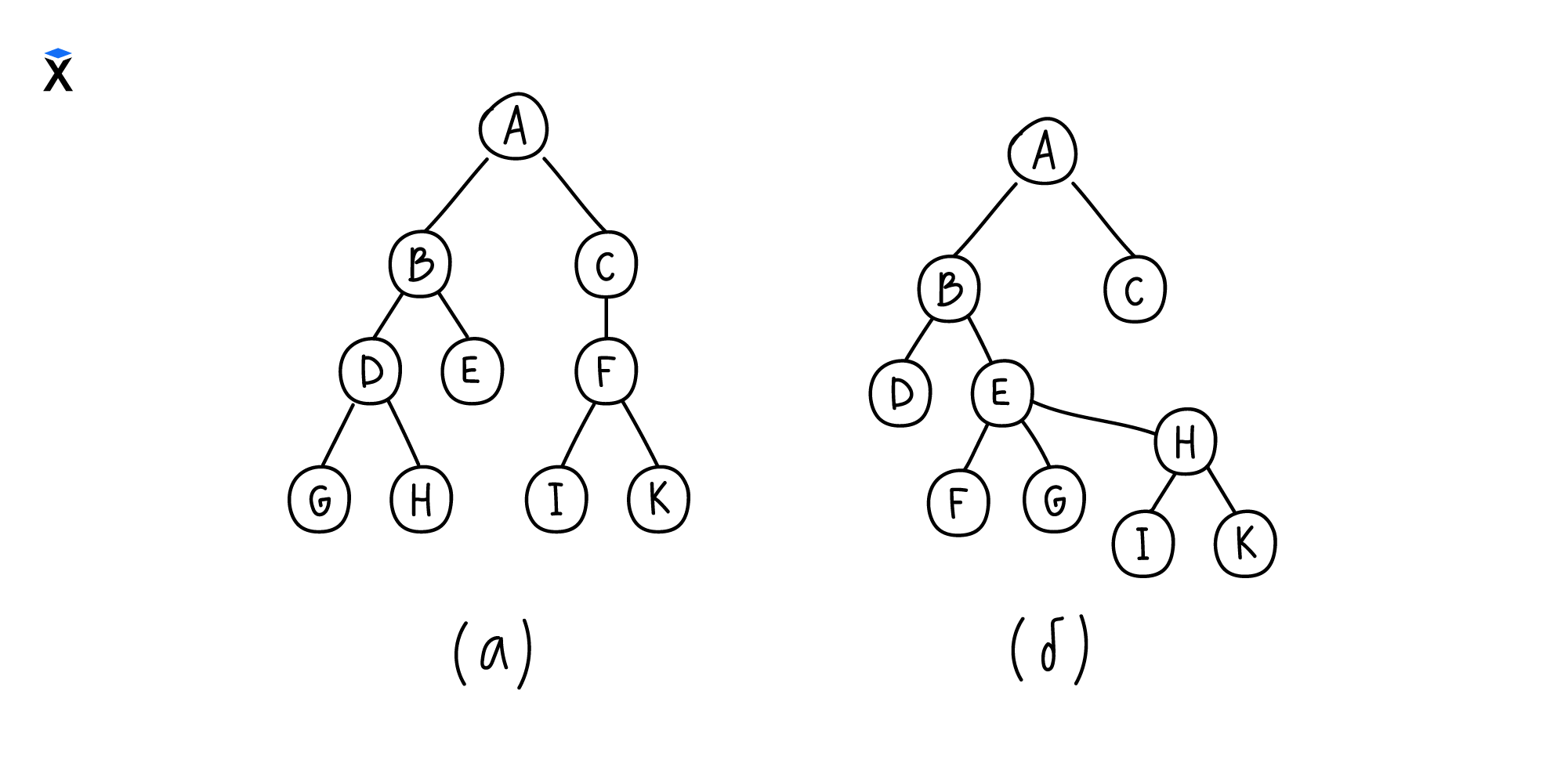
Дерево (а) — бинарное. У каждого его узла не более двух дочерних узлов, у каждого из которых тоже не более двух дочерних. Например, узлы E, G, H, I и K — листовые, значит, у них ноль дочерних узлов. У узла C только один дочерний узел, а у узлов A, B, D и F по два дочерних.

Как только правило двух дочерних нарушается, то дерево перестает относиться к классу бинарных. Так, дерево (б) не является бинарным, так как у узла E три дочерних узла.

Благодаря тому, что дочерних узлов всегда не больше двух, их называют правый и левый дочерние узлы.

Напомним, что есть завершенное и полное деревья. Для бинарных деревьев они приобретают следующий вид:

Завершенное бинарное дерево — это бинарное дерево, в котором каждый уровень, кроме последнего, полностью заполнен, а заполнение последнего уровня производится слева направо
Полное бинарное дерево — это бинарное дерево, в котором у каждого узла ноль или два дочерних узла

На практике чаще применяются два подвида бинарных деревьев: бинарные деревья поиска и бинарные кучи. Последние разберем в следующих уроках, а в этом сосредоточимся на первых.

Что такое бинарные деревья поиска

Бинарные деревья поиска отличаются от обычных бинарных деревьев тем, что хранят данные в отсортированном виде. Хранение значений внутри бинарного дерева поиска организовано в следующем виде:

Все значения в узлах левого дочернего поддерева меньше значения родительского узла
Все значения в узлах правого дочернего поддерева больше значения родительского узла
Каждый дочерний узел тоже является бинарным деревом поиска

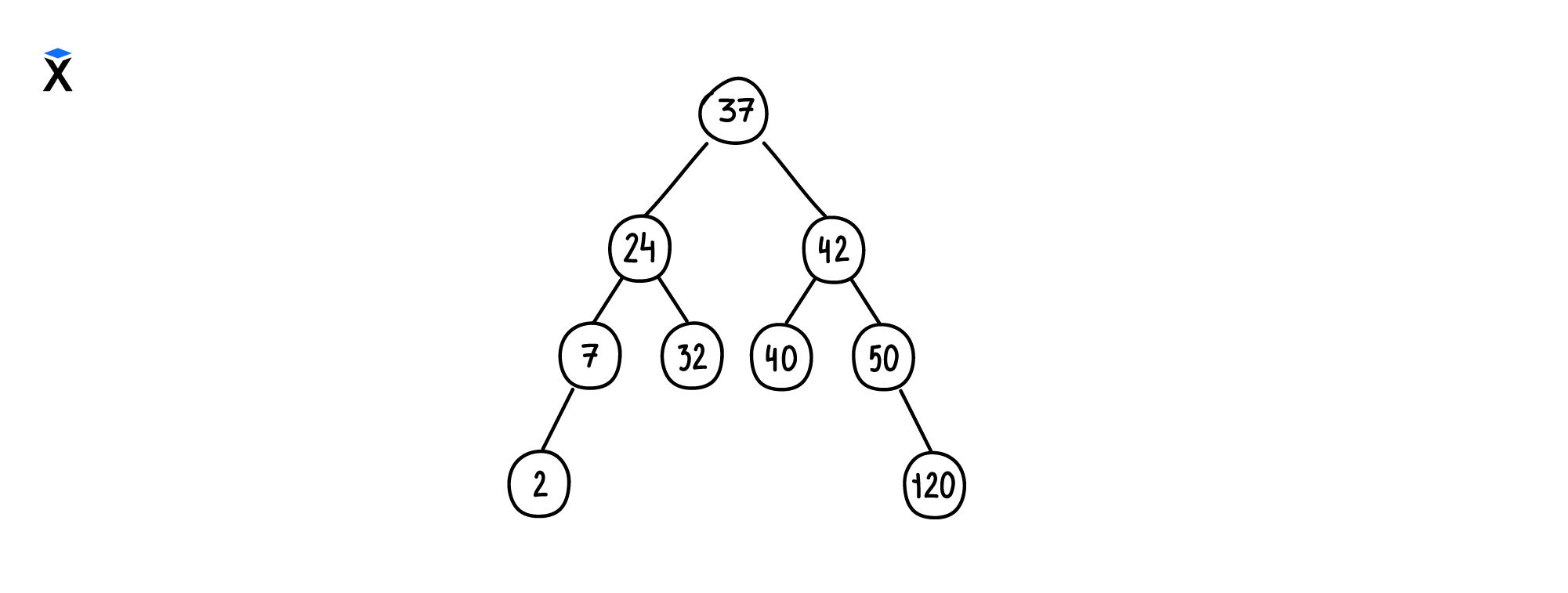
Благодаря такой структуре хранения данных поиск узла в бинарном дереве поиска занимает O(logN). Это значительно меньше, если хранить значения в списках — O(N).

Если использовать отсортированный массив для хранения данных, скорость поиска элементов сравняется. Но при оценке времени вставки хранение в массиве значительно проигрывает работе с деревьями — O(N) против O(logN) соответственно.

Такая высокая эффективность поиска в бинарном дереве поиска наблюдается только при сохранении его в сбалансированном состоянии — когда все уровни, кроме последнего полностью заполнены. Это значит, что любое добавление или удаление вершины может потребовать полное перестроение дерева. Более подробно об этой особенности мы поговорим в следующем уроке.

Рассмотрим на примере поиска элемента (10) сравнение операций поиска в отсортированном массиве, списке и бинарном дереве поиска:

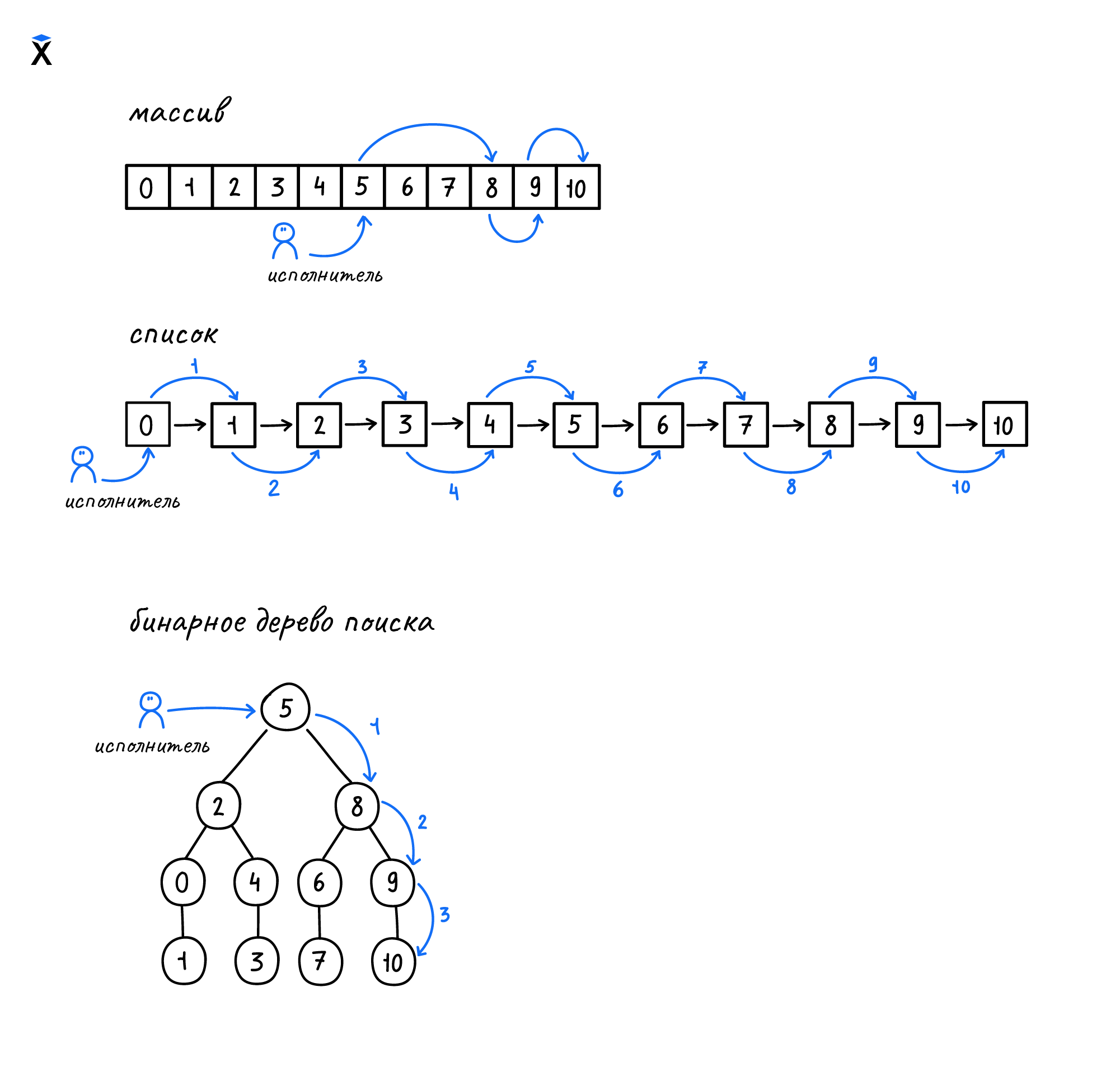
Для поиска в массиве применяется традиционный подход на основе половинного деления — метод дихотомии. На схеме можно видеть что аналогичная операция и на массиве, и на бинарном дереве поиска будет выполнена за три шага. В то же время поиск этого элемента на списке займет десять шагов.

Далее поговорим о структуре бинарных деревьев и начнем реализовывать бинарное дерево в коде.

Как бинарные деревья поиска реализуются в коде

Напомним свойства бинарных деревьев:

Должно быть не более двух дочерних узлов
Дочерние узлы тоже должны быть бинарными деревьями
Дочерние узлы называют левыми и правыми

В этом случае структура узла принимает следующий вид:

Javascript

class BinaryTreeNode {
  constructor(value, parent) {
    this.left = null // ссылка на левый дочерний узел
    this.right = null // ссылка на правый дочерний
    this.parent = parent // ссылка на родителя
    this.value = value // полезная нагрузка
  }
}

Java

public class BinaryTreeNode {
    public BinaryTreeNode left;
    public BinaryTreeNode right;
    public BinaryTreeNode parent;
    public Integer value;

    public BinaryTreeNode(Integer value, BinaryTreeNode parent) {
        this.parent = parent;
        this.value = value;
    }
}

Python

class BinaryTreeNode:
    def __init__(self, value, parent=None):
        self.left = None  # ссылка на левый дочерний узел
        self.right = None  # ссылка на правый дочерний узел
        self.parent = parent  # ссылка на родителя
        self.value = value  # полезная нагрузка

PHP

<?php
class BinaryTreeNode
{
    public ?BinaryTreeNode $left = null; // ссылка на левый дочерний узел
    public ?BinaryTreeNode $right = null; // ссылка на правый дочерний узел
    public ?BinaryTreeNode $parent = null; // ссылка на родителя
    public $value; // полезная нагрузка

    public function __construct($value, BinaryTreeNode $parent)
    {
        $this->parent = $parent;
        $this->value = $value;
    }
}

Теперь нам необходимо расширить наш класс и реализовать необходимые операции, чтобы взаимодействовать с проектируемым классом. Начнем с операции поиска узла.

С бинарными деревьями поиска можно выполнять следующие операции:

Искать узел
Вставлять узел
Удалять узел
Выполнять обход дерева

Разберем каждую операцию подробнее.

Поиск узла

Если искомое значение бинарного дерева поиска меньше значения узла, то оно может находиться только в левом поддереве. Искомое значение, которое больше значения узла, может быть только в правом поддереве. В таком случае мы можем применить рекурсивный подход и операция поиска будет выглядеть так:

Javascript

class BinaryTreeNode {
  // ...

  findNode(value) {
    let node = this
    while (node) {
      if (value == node.value) return node
      if (value < node.value) node = node.left
      if (value > node.value) node = node.right
    }

    return null
  }
}

Java

public class BinaryTreeNode {
    // ...

    public BinaryTreeNode findNode(Integer value) {
        BinaryTreeNode node = this;
        while (node != null) {
            if (Objects.equals(value, node.value)) {
                return node;
            }
            if (value < node.value) {
                node = node.left;
            } else {
                node = node.right;
            }
        }

        return null;
    }
}

Python

class BinaryTreeNode:
    ## ...

    def find_node(self, value):
        node = self
        while node:
            if value == node.value:
                return node
            if value < node.value:
                node = node.left
            if value > node.value:
                node = node.right
        return None

PHP

<?php
class BinaryTreeNode
{
    // ...

    public function findNode($value)
    {
        $node = $this;

        while ($node) {
            if ($value == $node->value) {
                return $node;
            }
            if ($value < $node->value) {
                $node = $node->left;
            }
            if ($value > $node->value) {
                $node = $node->right;
            }
        }

        return null;
    }
}

Вставка узла

Все значения меньше текущего значения узла надо размещать в левом поддереве, а большие — в правом. Чтобы вставить новый узел, нужно проверить, что текущий узел не пуст. Далее может быть два пути:

Если это так, сравниваем значение со вставляемым. По результату сравнения проводим проверку для правого или левого поддеревьев
Если узел пуст, создаем новый и заполняем ссылку на текущий узел в качестве родителя

Операция вставки использует рекурсивный подход аналогично операции поиска. Переведем данный алгоритм на язык JavaScript и получим следующий код метода вставки:

Javascript

class BinaryTreeNode {
  // ...

  insertNode(value) {
    return this.#insertNode(value, this)
  }

  #insertNode(value, parentNode) {
    if (value < parentNode.value) {
      if (parentNode.left == null) {
        parentNode.left = new BinaryTreeNode(value, parentNode)
      }
      else {
        this.#insertNode(value, parentNode.left)
      }
    }
    if (value > parentNode.value) {
      if (parentNode.right == null) {
        parentNode.right = new BinaryTreeNode(value, parentNode)
      }
      else {
        this.#insertNode(value, parentNode.right)
      }
    }
  }
}

Java

class BinaryTreeNode {
    // ...

    public void insertNode(int value) {
        insertNode(value, this);
    }

    private void insertNode(int value, BinaryTreeNode parentNode) {
        if (value < parentNode.value) {
            if (parentNode.left == null) {
                parentNode.left = new BinaryTreeNode(value, parentNode);
            } else {
                insertNode(value, parentNode.left);
            }
        }
        if (value > parentNode.value){
            if (parentNode.right == null){
                parentNode.right = new BinaryTreeNode(value, parentNode);
            } else {
                insertNode(value, parentNode.right);
            }
        }
    }
}

Python

class BinaryTreeNode:
    ## ...

    def insert_node(self, value):
        return self._insert_node(value, self)

    def _insert_node(self, value, parent_node):
        if value < parent_node.value:
            if parent_node.left is None:
                parent_node.left = BinaryTreeNode(value, parent_node)
            else:
                self._insert_node(value, parent_node.left)
        elif value > parent_node.value:
            if parent_node.right is None:
                parent_node.right = BinaryTreeNode(value, parent_node)
            else:
                self._insert_node(value, parent_node.right)

PHP

<?php
class BinaryTreeNode
{
    // ...

    public function insertNode($value)
    {
        $this->_innerInsertNode($value, $this);
    }

    public function _innerInsertNode($value, ?BinaryTreeNode $parentNode = null) {
        $parentNode = $parentNode ?? $this;

        if ($value < $parentNode->value) {
            if ($parentNode->left == null) {
                $parentNode->left = new BinaryTreeNode($value, $parentNode);
            } else {
                $this->_innerInsertNode($value, $parentNode->left);
            }
        }
        if ($value > $parentNode->value){
            if ($parentNode->right == null){
                $parentNode->right = new BinaryTreeNode($value, $parentNode);
            } else {
                $this->_innerInsertNode($value, $parentNode->right);
            }
        }
    }
}

Удаление узла

Чтобы удалить элемент в связном списке, нужно найти его и ссылку на следующий элемент перенести в поле ссылки на предыдущем элементе.

Если необходимо удалить корневой узел или промежуточные вершины и сохранить структуру бинарного дерева поиска, выбирают один из следующих двух способов:

Находим и удаляем максимальный элемент левого поддерева и используем его значение в качестве корневого или промежуточного узла
Находим и удаляем минимальный элемент правого поддерева и используем его значение в качестве корневого или промежуточного узла

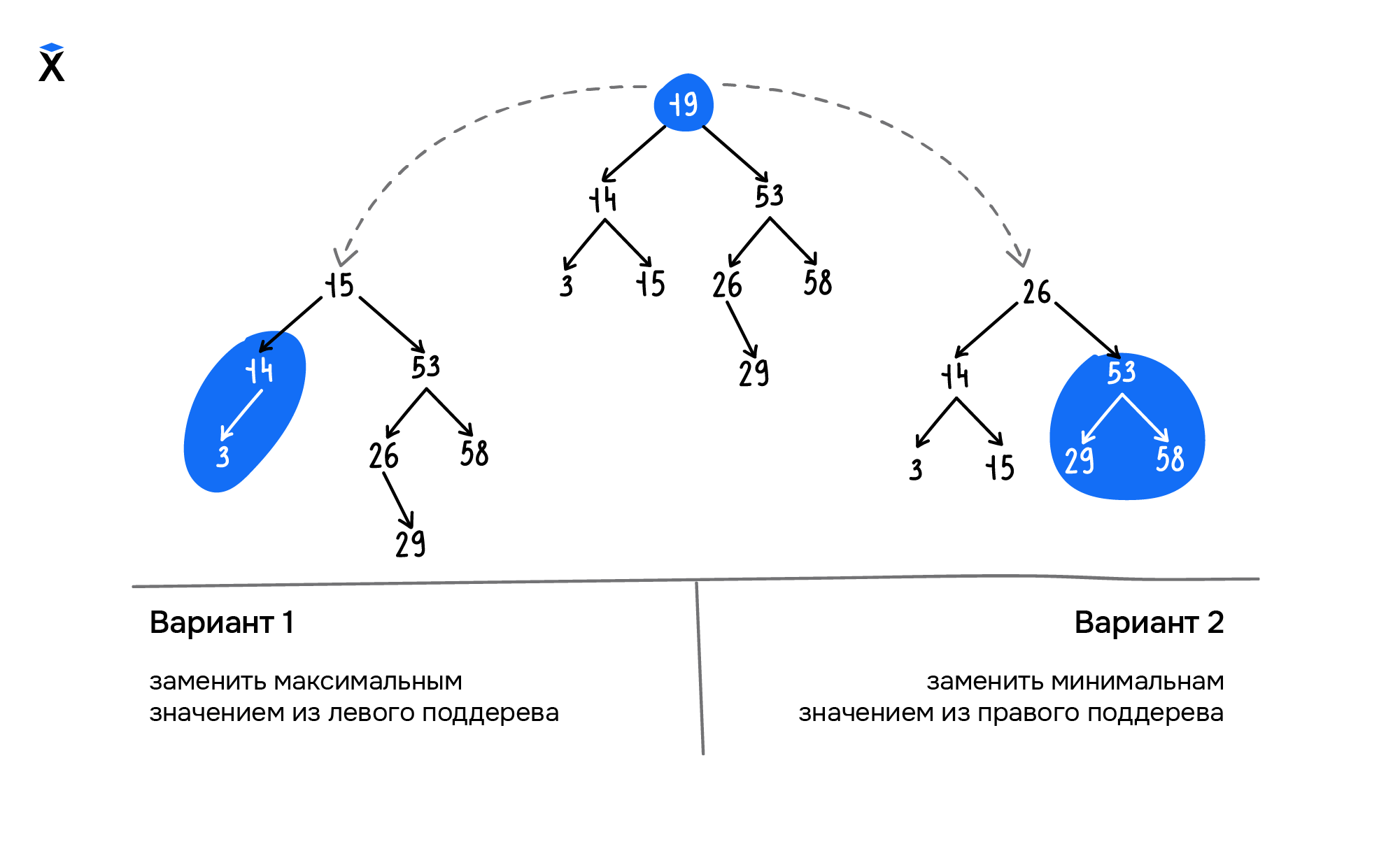
Оба варианта приемлемы для нашего дерева. Реализуем в коде второй вариант:

Javascript

class BinaryTreeNode {
  // ...

  removeNode(value) {
    return this.#removeNode(value, this)
  }

  #removeNode(value, node) {
    if (node == null) return null

    if (value < node.value) {
      node.left = this.#removeNode(value, node.left)
    }
    else if (value > node.value) {
      node.right = this.#removeNode(value, node.right)
    }
    else {
      if (node.left == null) return node.right
      if (node.right == null) return node.left
    }

    let original = node
    node = node.right
    while (node.left) {
      node = node.left
    }

    node.right = this.#removeMin(original.right)
    node.left = original.left
  }

  #removeMin(node) {
    if (node.left === null) {
      return node.right
    }
    node.left = this.#removeMin(node.left)
    return node
  }
}

Java

class BinaryTreeNode {
    // ...

    public void removeNode(int value) {
        removeNode(value, this);
    }

    private BinaryTreeNode removeNode(int value, BinaryTreeNode node) {
        if (node == null) {
            return null;
        }

        if (value < node.value) {
            node.left = removeNode(value, node.left);
        } else if (value > node.value) {
            node.right = removeNode(value, node.right);
        } else {
            if (node.left == null) {
                return node.right;
            }
            if (node.right == null) {
                return node.left;
            }
        }

        BinaryTreeNode original = node;
        node = node.right;
        while (node.left != null) {
            node = node.left;
        }

        node.right = removeNode(value, original.right);
        node.left = original.left;
        return node;
    }
}

Python

class BinaryTreeNode:
    ## ...

    def remove_node(self, value):
        return self._remove_node(value, self)

    def _remove_node(self, value, node):
        if node is None:
            return None

    if value < node.value:
        node.left = self._remove_node(value, node.left)
        return node
    elif value > node.value:
        node.right = self._remove_node(value, node.right)
        return node
    else:
        if node.left is None:
            return node.right
        elif node.right is None:
            return node.left
        else:
            original = node
            node = node.right
            while node.left:
                node = node.left
            node.right = self._remove_node(node.value, original.right)
            node.left = original.left
            return node

PHP

<?php
class BinaryTreeNode
{
    // ...
    public function removeNode($value, ?BinaryTreeNode $node = null) {
        if ($node == null) {
            return null;
        }

        if ($value < $node->value) {
            $node->left = $this->removeNode($value, $node->left);
        }
        else if ($value > $node->value) {
            $node->right = $this->removeNode($value, $node->right);
        }
        else {
            if ($node->left == null) {
                return $node->right;
            }
            if ($node->right == null) {
                return $node->left;
            }
        }

        $original = $node;
        $node = $node->right;
        while ($node->left != null) {
            $node = $node->left;
        }

        $node->right = $this->removeNode($original->right);

        $node->left = $original->left;
        return $node->right;
    }
}

Реализация первого варианта будет выглядеть практически идентично. Только есть исключение: мы будем обходить правое поддерево и искать максимальное значение узла вместо минимального.

Для деревьев также существуют специфические операции, важнейшая из которых — обход дерева. Рассмотрим эту операцию подробнее.

Обход деревьев

Когда мы поработали с деревом и нам нужно его сохранить в файл или вывести в печать, нам больше не нужен древовидный формат. Здесь мы прибегаем к обходу дерева — последовательное единоразовое посещение всех вершин дерева.

Существуют такие три варианта обхода деревьев:

Прямой обход (КЛП): корень → левое поддерево → правое поддерево
Центрированный обход (ЛКП): левое поддерево → корень → правое поддерево
Обратный обход (ЛПК): левое поддерево → правое поддерево → корень

Такие обходы называются поиском в глубину*. На каждом шаге итератор пытается продвинуться вертикально вниз по дереву перед тем, как перейти к родственному узлу — узлу на том же уровне. Еще есть поиск в ширину — обход узлов дерева по уровням: от корня и далее:

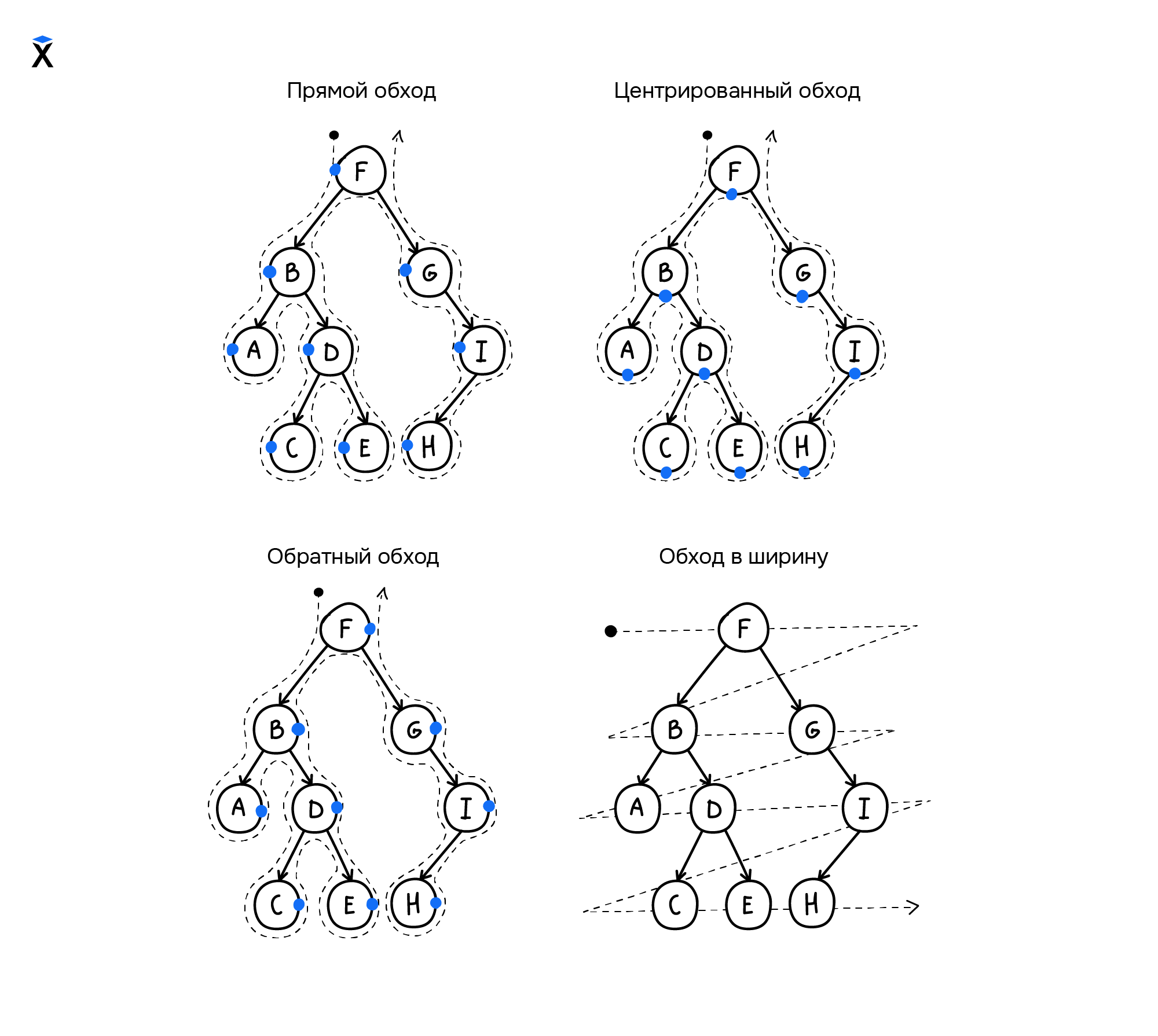
Реализация поиска в глубину может осуществляться или с использованием рекурсии, или с использованием стека. А поиск в ширину реализуется за счет использования очереди:

Javascript

class BinaryTreeNode {
    // ...

    traverseRecursive(node) {
        if (node != null) {
            console.log(`node = ${node.val}`);
            traverseRecursive(node.left);
            traverseRecursive(node.right);
        }
    }

    traverseWithStack() {
        let stack = [];
        stack.push(this);
        while (stack.length > 0) {
            let currentNode = stack.pop();

    console.log(`node = ${currentNode.val}`);
    if (currentNode.right != null) {
        stack.push(currentNode.right);
    }
    if (currentNode.left != null) {
        stack.push(currentNode.left);
    }


    traverseWithQueue() {
        let queue = [];
        queue.push(this.root);
        while (queue.length > 0) {
            let currentNode = queue.shift();
            console.log(`node = ${currentNode.val}`);
            if (currentNode.left) {
                queue.push(currentNode.left);
            }
            if (currentNode.right) {
                queue.push(currentNode.right);
            }
        }
    }
}

Java

public class BinaryTreeNode {
    // ...

    public void traverseRecursive() {
        traverseRecursive(this);
    }

    private void traverseRecursive(BinaryTreeNode node) {
        if (node != null) {
            System.out.println("node = " + node.value);
            traverseRecursive(node.left);
            traverseRecursive(node.right);
        }
    }

    public void traverseWithStack() {
        Deque<BinaryTreeNode> stack = new ArrayDeque<>();
        stack.push(this);
        while (stack.size() > 0) {
            BinaryTreeNode currentNode = stack.pop();

            System.out.println("node = " + currentNode.value);

            if (currentNode.right != null) {
                stack.push(currentNode.right);
            }
            if (currentNode.left != null) {
                stack.push(currentNode.left);
            }
        }
    }

    public void traverseWithQueue() {
        Deque<BinaryTreeNode> queue = new ArrayDeque<>();
        queue.push(this);
        while (queue.size() > 0) {
            BinaryTreeNode currentNode = queue.removeFirst();
            System.out.println("node" + currentNode.value);
            if (currentNode.left != null ){
                queue.push(currentNode.left);
            }
            if (currentNode.right != null) {
                queue.push(currentNode.right);
            }
        }
    }
}

Python

def traverse_recursive(node):
    if node is not None:
        print(f"node = {node.value}")
        traverse_recursive(node.left)
        traverse_recursive(node.right)

def traverse_with_stack(root):
    stack = []
    stack.append(root)
    while len(stack) > 0:
        current_node = stack.pop()
        print(f"node = {current_node.value}")
        if current_node.right is not None:
            stack.append(current_node.right)
        if current_node.left is not None:
            stack.append(current_node.left)

def traverse_with_queue(root):
    queue = []
    queue.append(root)
    while len(queue) > 0:
        current_node = queue.pop(0)
        print(f"node = {current_node.value}")
        if current_node.left:
            queue.append(current_node.left)
        if current_node.right:
            queue.append(current_node.right)

PHP

<?php

class BinaryTreeNode
{
    // ...

    public function traverseRecursive()
    {
        $this->traverseRecursiveInner($this);
    }

    private function traverseRecursiveInner($node)
    {
        if ($node != null) {
            echo "node = {$node->value}\n";
            $this->traverseRecursiveInner($node->left);
            $this->traverseRecursiveInner($node->right);
        }
    }

    public function traverseWithStack()
    {
        $stack = new SplStack();
        $stack->push($this);
        while (!$stack->isEmpty()) {
            $currentNode = $stack->pop();

            echo "node = {$currentNode->value}\n";

            if ($currentNode->right != null) {
                $stack->push($currentNode->right);
            }
            if ($currentNode->left != null) {
                $stack->push($currentNode->left);
            }
        }
    }

    public function traverseWithQueue()
    {
        $queue = new SplQueue();
        $queue->enqueue($this);
        while (!$queue->isEmpty()) {
            $currentNode = $queue->dequeue();
            echo "node = {$currentNode->value}\n";
            if ($currentNode->left != null) {
                $queue->enqueue($currentNode->left);
            }
            if ($currentNode->right != null) {
                $queue->enqueue($currentNode->right);
            }
        }
    }
}

Выводы

В этом уроке мы познакомились с бинарными деревьями — структурой, которая лежит в основе многих других типов данных: множеств, куч, очередей с приоритетом. Еще мы подробно разобрали ключевой их подвид — бинарные деревья поиска и изучили методы работы с ними. Они позволят эффективно искать и обновлять большие объемы данных.