- Что такое деревья и для чего они нужны
- Какие узлы есть в деревьях
- Какие формы деревьев бывают
- Как могут выглядеть деревья
- Выводы
Иерархические структуры окружают нас везде — например, структура управления предприятием, адреса, содержания в книгах. Иерархия встречается и в программировании, например, в работе со стандартными типами данных, такими как массивы. Так как такие данные нельзя разместить линейно, программисты используют деревья. Они считаются одной из важнейших нелинейных структур, которые встречаются при работе с алгоритмами.
В этом уроке мы поговорим о деревьях, узнаем, какие проблемы они решают, и какие характеристики и способы представления деревьев существуют.
Что такое деревья и для чего они нужны
Деревья используют, чтобы отразить в памяти компьютера иерархические взаимосвязи. Их применяют для реестра Windows, XML-документов, DOM-структур HTML-страниц, родословных, каталогов запчастей или файловых систем. Например, так файловую структуру видят конечные пользователи:
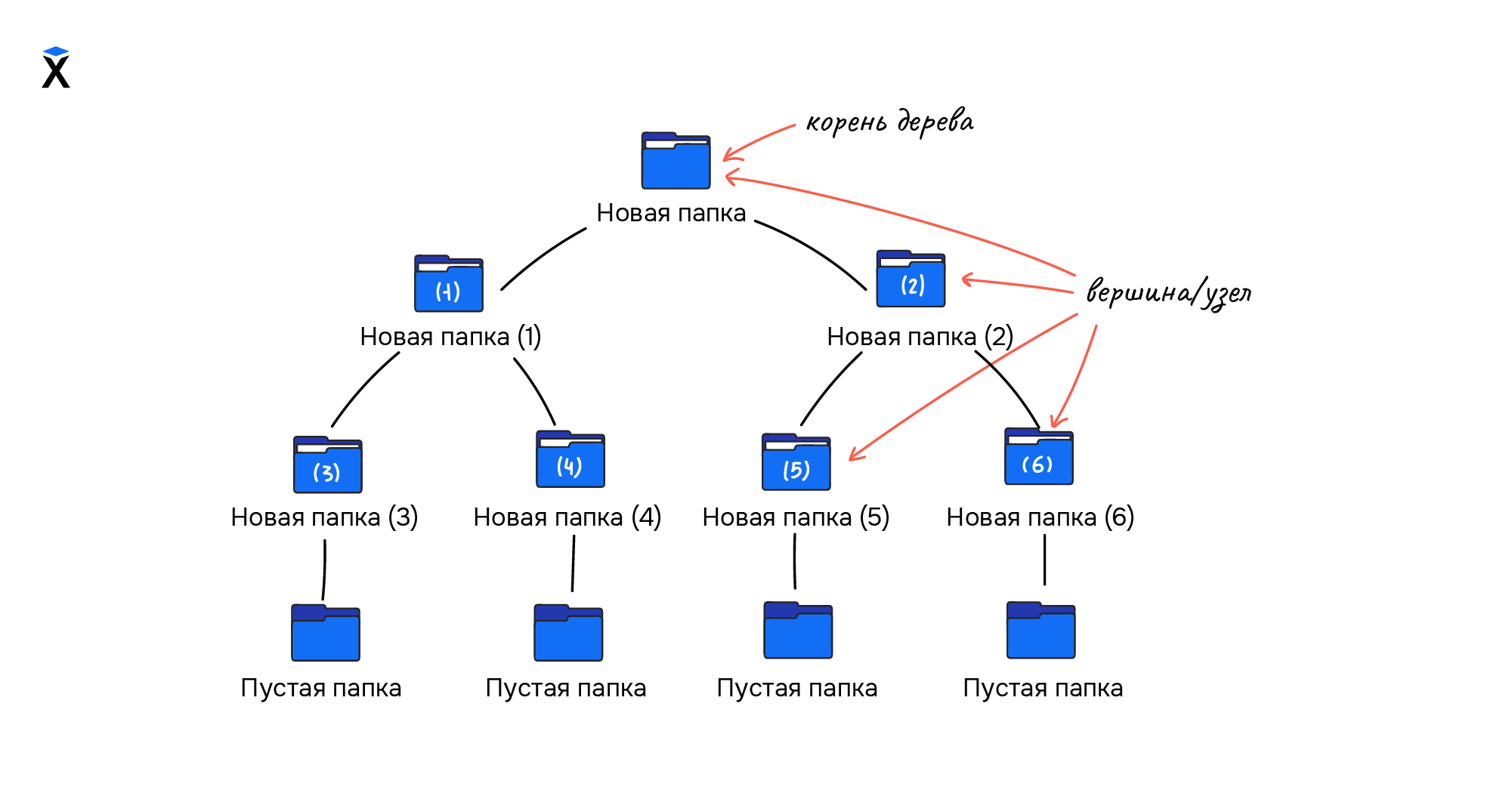
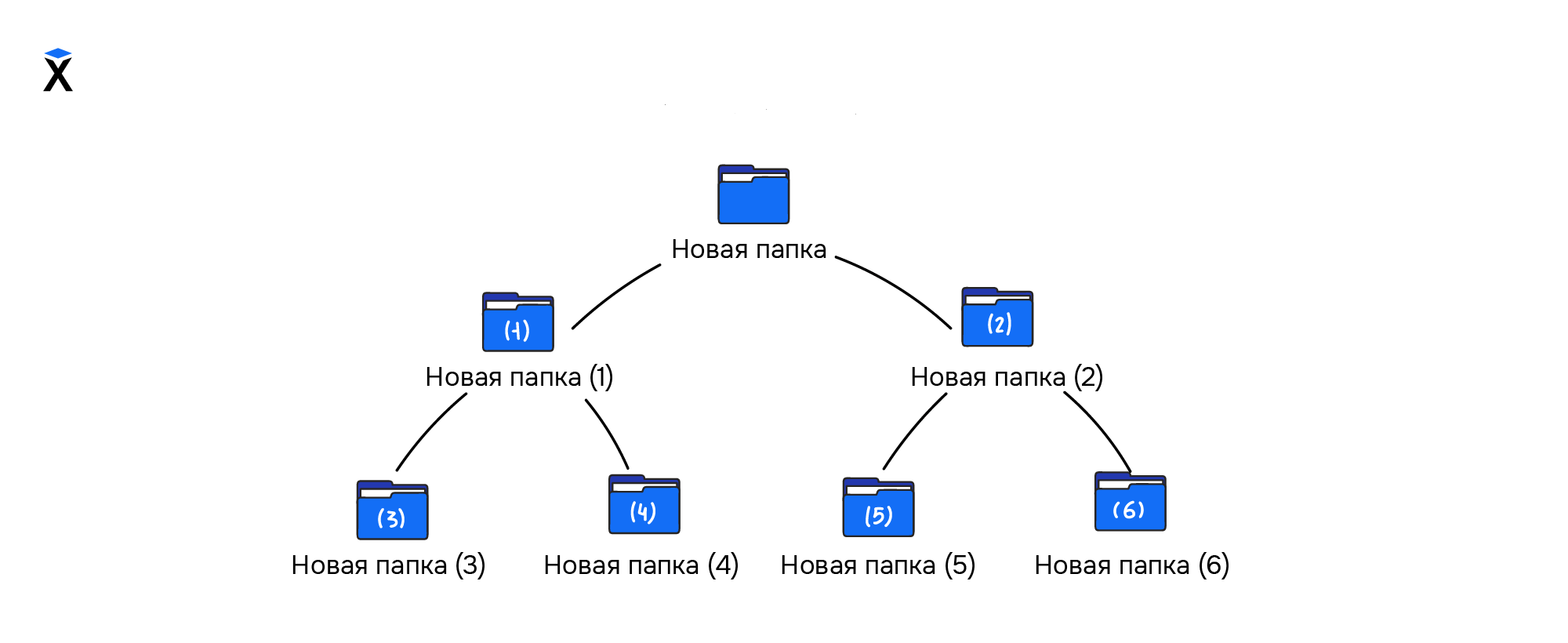
При этом для программистов она выглядит иначе:
Это древовидное представление структуры. Из этой схемы можно сделать вывод, что дерево — это конечное множество, которое состоит из вершин или узлов, а еще есть выделенный узел — корень дерева. В примере выше вершины — это все папки, а корень дерева — «Новая папка».
Каждый узел содержит данные и ссылки на другие непересекающиеся между собой деревья. В этом случае каждая папка в дереве, от которой исходят другие данные, является для них корневым узлом. При этом эти данные образуют поддерево основного дерева.
Помимо представления иерархических взаимосвязей, деревья применяют в следующих случаях:
- Организация быстрого поиска в отсортированных данных, например, в индексах баз данных
- Кластеризация данных. Возможность разбивать данные на кластеры применяется в базах данных и машинном обучении
- Решение сложных арифметических выражений. Дерево используется, чтобы хранить порядок выполнения операций, значений аргументов и промежуточных результатов
- Алгоритмы принятия решений. Дерево решений — инструмент интеллектуального анализа данных и проведения предсказаний. Он считается более простым в работе инструментом, чем нейросети, так как формулирует правила на естественном языке
- Сетевое взаимодействие. Деревья используют для маршрутизации и работы механизмов определения IP-адресов по URL сайта, например, DNS-сервера
Деревья часто используют в проектах по разработке программ. Как результат — разработчики выделили терминологию описания узлов и формы деревьев.
Какие узлы есть в деревьях
Так как внешний вид дерева схож с генеалогическим деревом, термины генеалогии применяются и в программировании. Например, в отношении алгоритмических деревьев можно услышать такие термины, как «основатель династии», «мама», «ребенок», «брат», «двоюродный дядя». При этом существуют стандартизированные именования для отношений узлов:
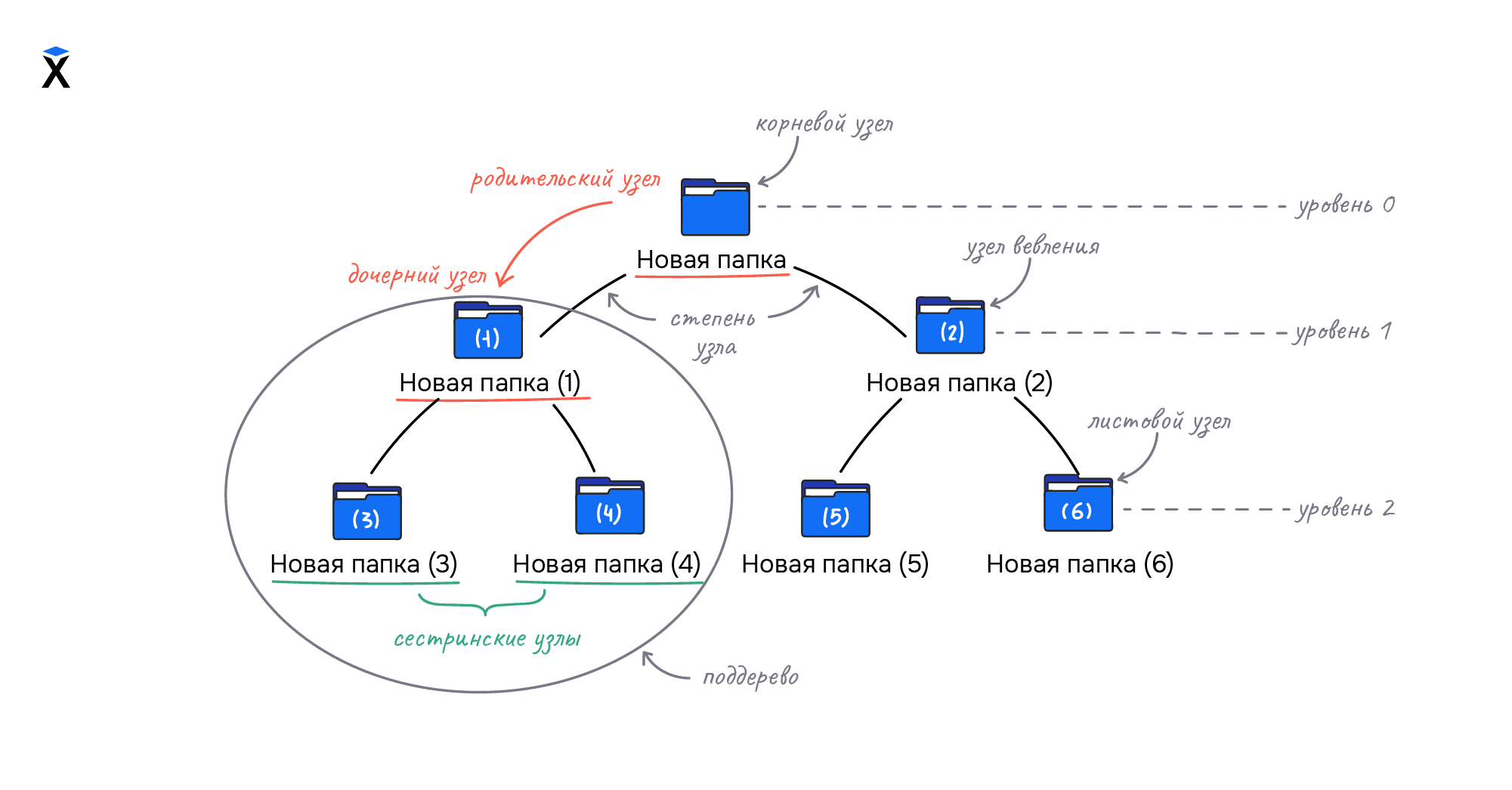
- Родительский узел или предок — узел, который находится на первом уровне иерархии
- Дочерний узел или потомок — узел, на который есть ссылки из рассматриваемого узла
- Корневой узел — узел, на который нет ссылок из других узлов
- Сестринские узлы — два узла, у которых общие родители
- Листовой узел, лист дерева или терминальный узел — узел, у которого количество поддеревьев равно нулю
- Узел ветвления или внутренняя вершина — узел, у которого есть дочерние структуры
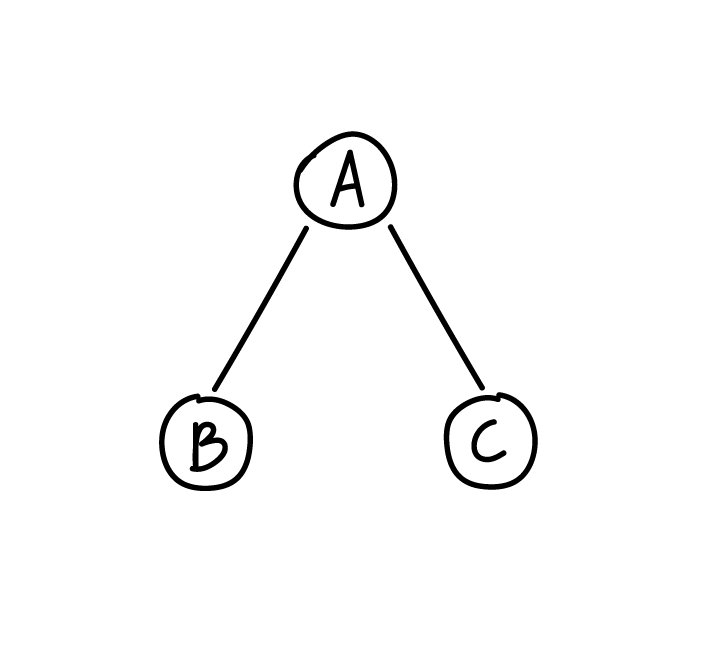
Количество поддеревьев у узла называется его степенью. Максимальное значение степени узла — *степень дерева**. Если степень дерева равна двум, значит, у каждого узла может быть не более двух потомков:
Какие формы деревьев бывают
Из-за определенных особенностей задач и алгоритмов, разработчики применяют разные формы деревьев со своими особенностями организации вершин:
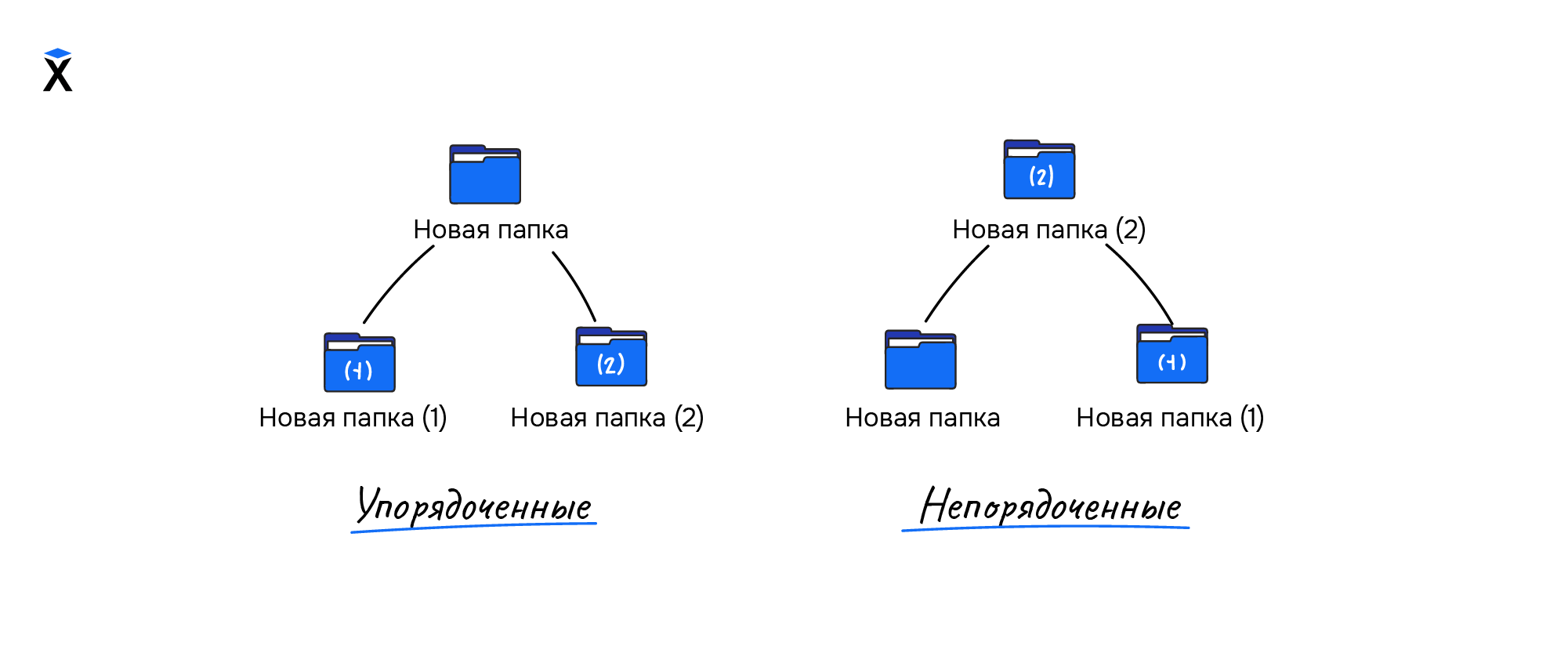
- Упорядоченное дерево — дерево, в котором все вершины отсортированы. Такие деревья еще называются плоскими, так как при последовательном обходе вершин получится отсортированный массив:
Далее в курсе мы будем считать все деревья упорядоченными, если в условии не сказано обратное.
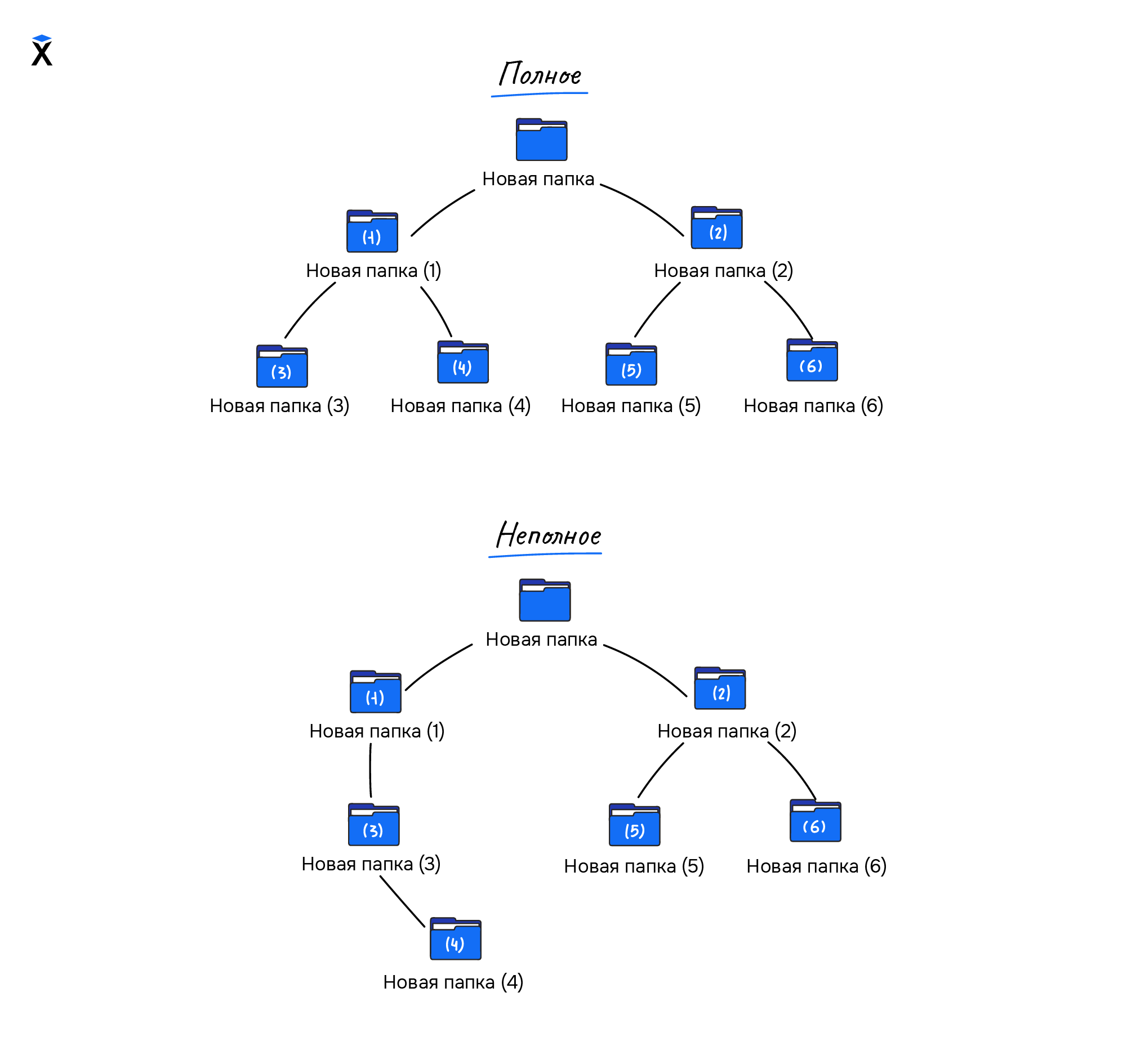
- Полное дерево — дерево, в котором количество дочерних узлов у каждой внутренней вершины равно степени дерева:
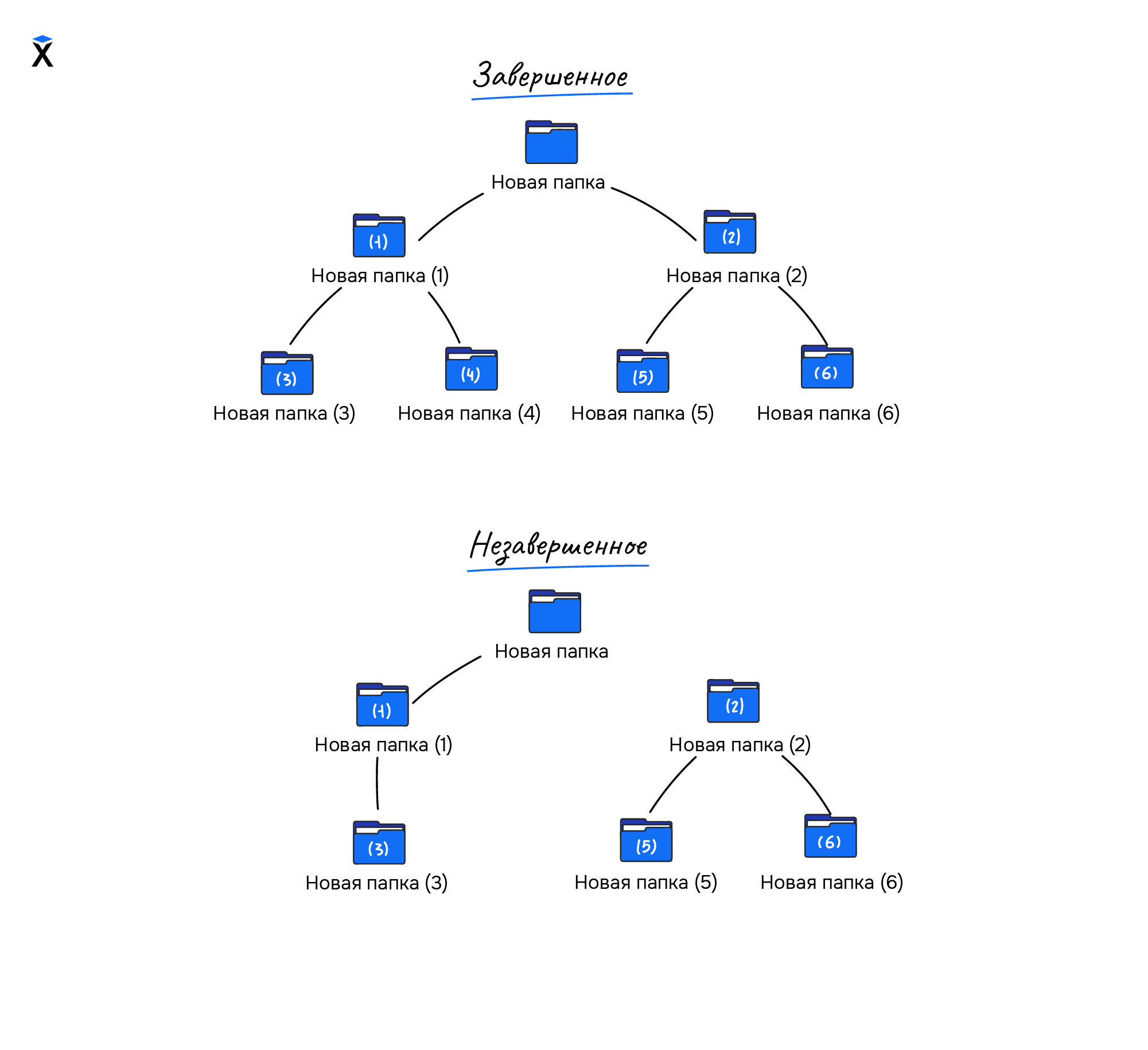
- Завершенное дерево – дерево, у которого каждый уровень, кроме последнего, является полным:
- Идеальное дерево — полное дерево, у которого все терминальные узлы располагаются на одном уровне:
Мы познакомились с основной терминологией, которая используется при работе с деревьями. Теперь рассмотрим, какие есть способы представления деревьев в графическом виде и в коде.
Как могут выглядеть деревья
Чтобы изображать иерархические структуры, используют следующие варианты:
- Древовидное схематическое представление
- Круги Эйлера
- Списки с отступами
- Код
Разберем каждый способ изображения дерева.
Древовидное схематическое представление
В качестве основного способа представления деревьев используют имена, номера вершин или содержимое полезных данных узла. Они соединяются линиями, которые обозначают связи между вершинами:
Этот способ похож на природные деревья, только в информатике корень дерева обычно рисуется вверху схемы.
Круги Эйлера
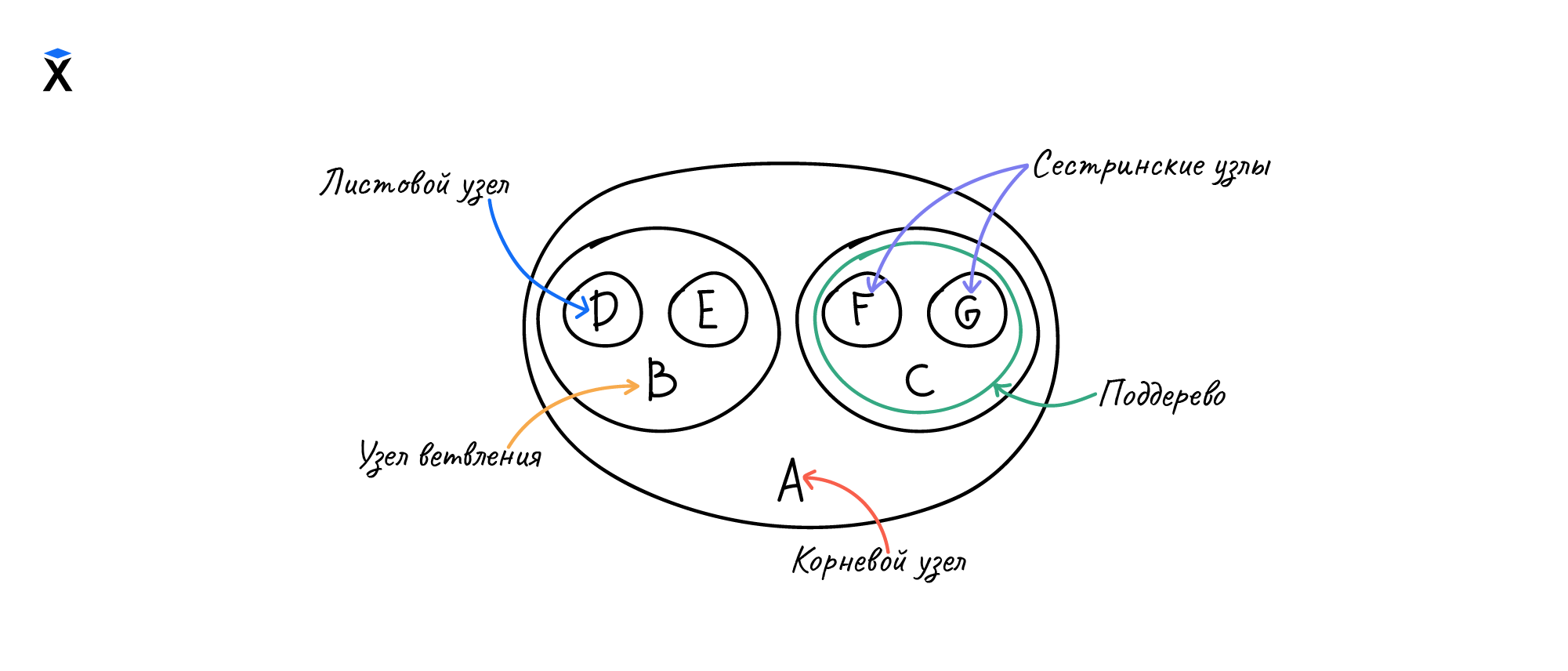
Мы можем изобразить алгоритмическое дерево по правилам теории множеств с помощью кругов Эйлера:
Данный способ на практике встречается достаточно редко, так как поддеревья обычно не пересекаются между собой. В такой ситуации использование схематичного представления более наглядно для человека.
Списки с отступами
Иерархическую связь можно изображать через пронумерованный список с отступами, где отступ или номер строки будут означать ее уровень:
Такой формат используют при работе с книгой, так как оглавление — это дерево.
Код
Чтобы работать с деревьями, их нужно уметь не только рисовать, но и хранить в памяти компьютера.
В виде кода мы получаем следующий класс узла:
Javascript
class BinaryTreeNode {
constructor(value, parent) {
this.child1 = null
this.child2 = null
this.parent = parent
this.value = value
}
}
Java
class BinaryTreeNode {
public BinaryTreeNode child1 = null;
public BinaryTreeNode child2 = null;
public BinaryTreeNode parent;
public Object value;
BinaryTreeNode(Object value, BinaryTreeNode parent) {
this.parent = parent;
this.value = value;
}
}
Python
class BinaryTreeNode:
def __init__(self, value, parent=None):
self.child1 = None
self.child2 = None
self.parent = parent
self.value = value
PHP
<?php
class BinaryTreeNode
{
public ?BinaryTreeNode $child1 = null;
public ?BinaryTreeNode $child2 = null;
public ?BinaryTreeNode $parent = null;
public $value;
public function __construct($value, BinaryTreeNode $parent)
{
$this->parent = $parent;
$this->value = $value;
}
}
Чтобы организовать из узла дерево, нужно добавить методы, которые заполняют ссылки на поддеревья child1 и child2. Как реализуются деревья в коде, разберем подробно в следующих уроках.
Прежде чем писать код дерева, разработчики часто изображают иерархию графически, чтобы видеть полную картину взаимосвязей.
Выводы
Мы познакомились с такой структурой данных как деревья. Они используются, чтобы хранить информацию в иерархическом виде, индексировать и кластеризировать большие последовательности данных.
В этом уроке мы также познакомились с основными обозначениями узлов, а также различными формами деревьев. Еще рассмотрели способы представления дерева — можно изображать иерархию с помощью схемы, кругов Эйлера, списком с отступами, а также в коде.
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.