Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажером

Префиксные деревья Алгоритмы на деревьях

Древовидные структуры можно использовать для хранения и организации, причем не только цельных, но и группируемых данных.

Например, такие данные могут состоять из последовательности одинаковых символов. Рассмотрим в качестве исходной точки несколько слов из толкового словаря:

ОБЕСПЕЧИВАТЬ. Несовершенный вид к «обеспечить»…​

ОБЕСПЕЧИТЬ. Совершенный вид к «обеспечивать». Предоставить материальные средства для жизни…​

ОБЕСПЕЧИТЬСЯ. Совершенный вид к «обеспечиваться». Запастись, стать обеспеченным…​

Как можно видеть из примера, существует несколько слов, которые начинаются на одну и ту же последовательность символов. В нашем случае у слов один и тот же корень, меняются только суффиксы и окончания.

В информатике часть последовательности данных, которая не меняется и находится перед суффиксом, называется префиксной частью.

В этом уроке мы более подробно познакомимся с принципами работы префиксных деревьев, их производными версиями и механизмами работы.

Зачем нужны префиксные деревья

При помощи одинаковых префиксов можно сгруппировать наши слова в следующем виде:

Группировка слов

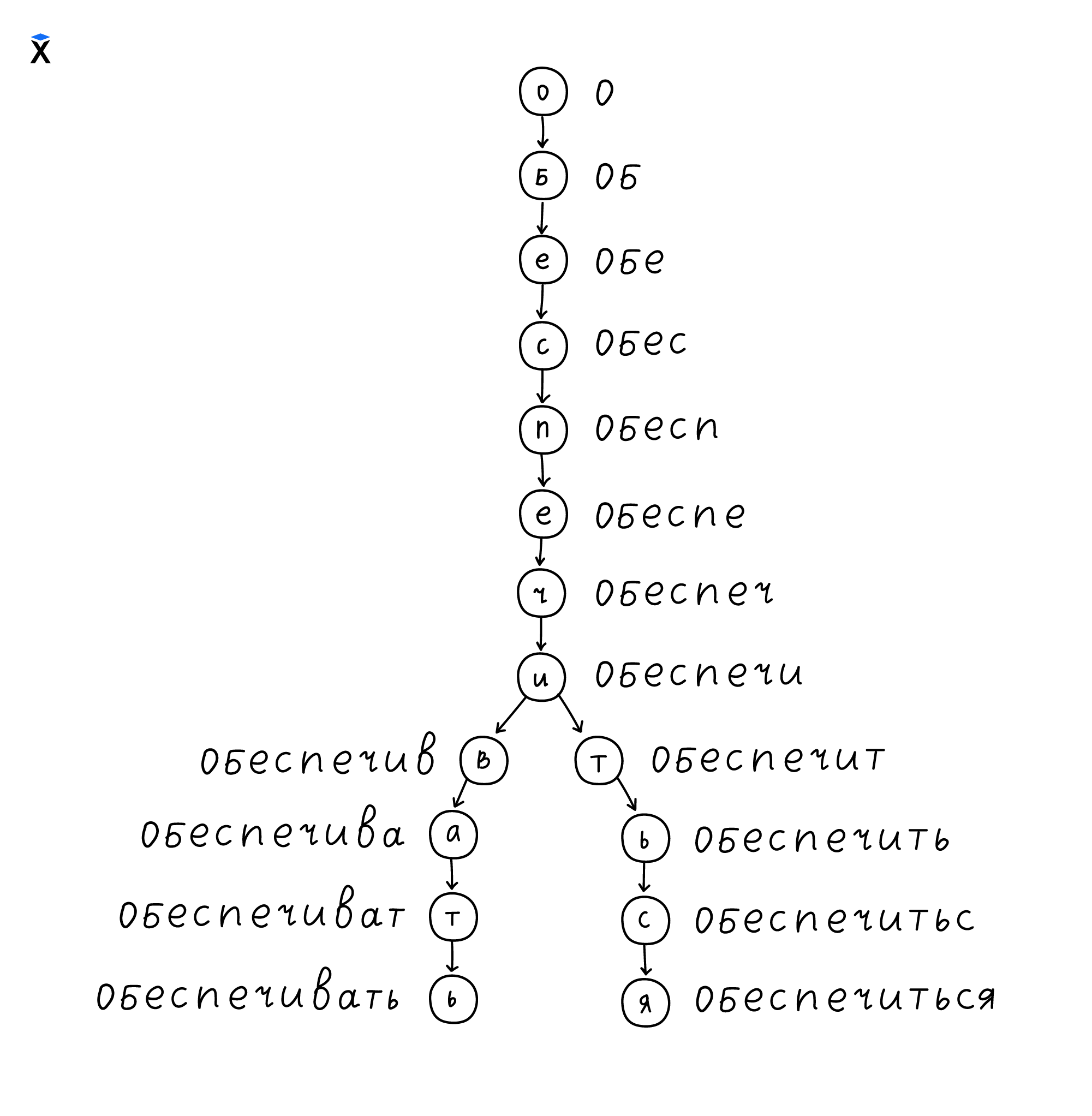
Префиксные деревья специально разработаны, чтобы помогать нам организовывать, хранить и группировать данные в таком виде. Префиксное дерево для нашего примера будут иметь следующий вид:

Префиксное дерево

Префиксные деревья помогают прогнозировать пользовательский ввод — например, предлагая слово, наиболее близкое по составу введенных букв. Так работают системы проверки орфографии или дополнитель кода в среде разработки.

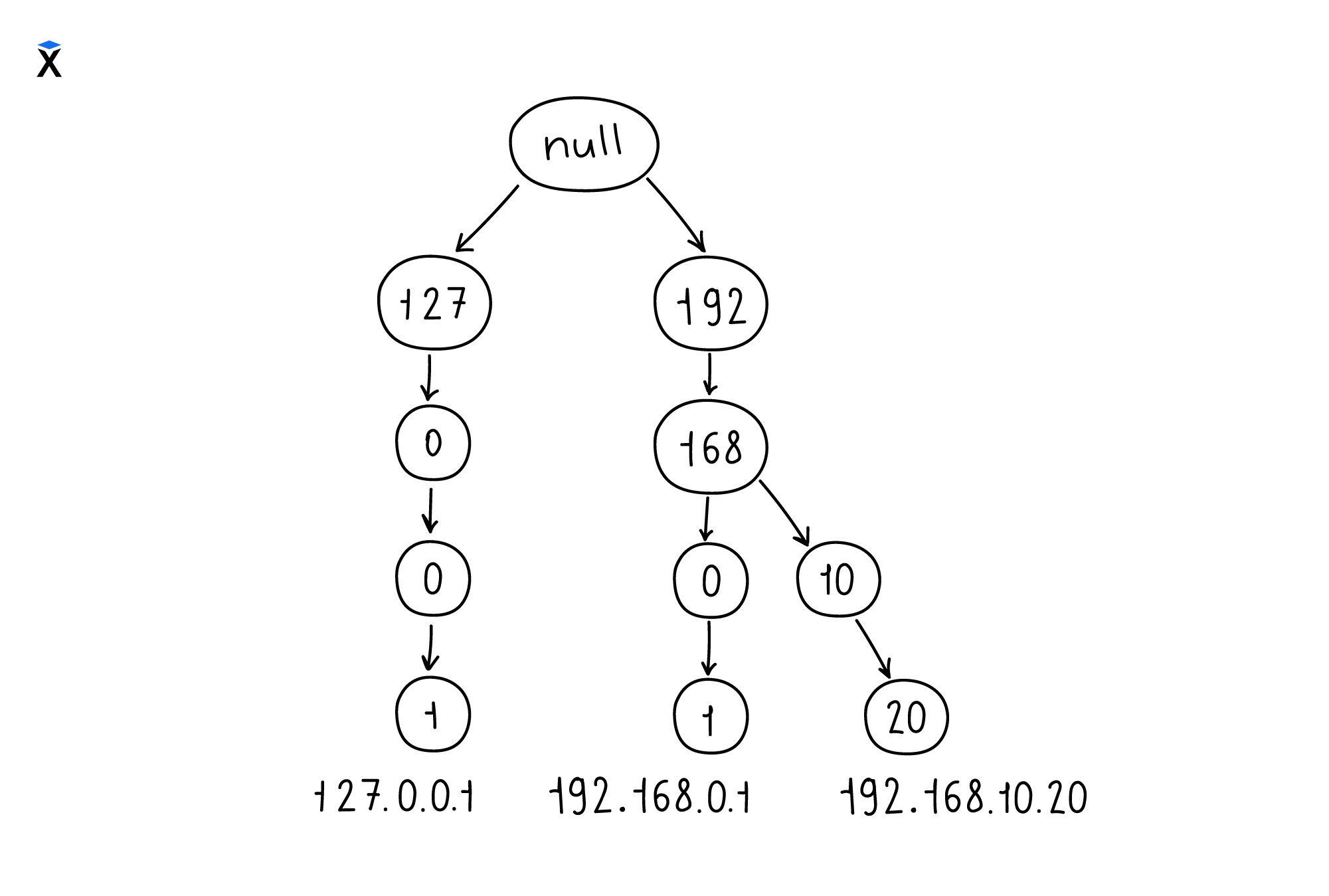
Механизм префиксов нашел свое место и в работе интернет-маршрутизации. Там он помогает эффективно хранить IP-адреса, группируемые по префиксам:

IP-адреса

Как устроены префиксные деревья

В качестве примера префиксного дерева рассмотрим хранение слов или некоторых ассоциативных массивов.

Префиксным деревом называется дерево, в котором каждая вершина помечена некоторой буквой и имеет дополнительный признак терминальности. Если мы читаем вершины по порядку, мы получаем последовательность символов, соответствующую некоторому слову.

Если полученная последовательность заканчивается признаком терминальности, то такое слово считается существующим в этой структуре данных.

При этом два узла не могут быть связаны с общим предком с помощью одной и той же буквы.

Операции над деревом

Для начала представим префиксное дерево в виде кода на JavaScript:

class Trie {
    constructor(key, parent = null) {
        this.key = key;
        this.children = {};
        this.parent = parent;
        this.end = false;
    }

    getWord() {
        let output = [];
        let node = this;

        while (node !== null) {
            output.unshift(node.key);
            node = node.parent;
        }
        return output.join('');
    }
}
Java 
public class Trie {
    private char key;
    private Map<Character, Trie> children;
    private Trie parent;
    private boolean end;

    public Trie(char key, Trie parent) {
        this.key = key;
        this.children = new HashMap<>();
        this.parent = parent;
        this.end = false;
    }

    public String getWord() {
        StringBuilder output = new StringBuilder();
        Trie node = this;
        while (node != null) {
            output.insert(0, node.key);
            node = node.parent;
        }
        return output.toString();
    }
}
Python 
class Trie:
    def __init__(self, key, parent=None):
        self.key = key
        self.children = {}
        self.parent = parent
        self.end = False

    def get_word(self):
        output = []
        node = self
        while node is not None:
            output.insert(0, node.key)
            node = node.parent
        return ''.join(output)
PHP 
<?php
class Trie {
    public $key;
    public $children;
    public $parent;
    public $end;

    public function __construct($key, $parent = null) {
        $this->key = $key;
        $this->children = [];
        $this->parent = $parent;
        $this->end = false;
    }

    public function getWord() {
        $output = [];
        $node = $this;
        while ($node !== null) {
            array_unshift($output, $node->key);
            $node = $node->parent;
        }
        return implode('', $output);
    }
}

С префиксными деревьями можно проводить разные операции, в том числе поиск слов, вставка нового слова и удаление слова. Разберем их подробнее.

Поиск слова в дереве

Для выполнения поиска сперва необходимо обратиться к корневой вершине. Обычно считается, что значение корневой вершины равно пустоте.

Далее мы перемещаемся по указателям, соответствующим каждой следующей букве в искомом слове.

Как только все переходы будут выполнены, нужно выполнить проверку на наличие флага терминальности в поле end нашего класса.

Если флаг конца слова присутствует, то поиск считаем завершенным успешно — искомое слово найдено.

Представим теперь эту операцию в виде метода:

class Trie {
  //...
  contains(word) {
        let node = this;
        for (let i = 0; i < word.length; i++) {
            if (node.children[word[i]]) {
                node = node.children[word[i]];
            } else {
                return false;
            }
        }
        return node.end;
    }
}
Java 
class Trie {
    //...
    public boolean contains(String word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            char ch = word.charAt(i);
            if (node.children.containsKey(ch)) {
                node = node.children.get(ch);
            } else {
                return false;
            }
        }
        return node.end;
    }
}
Python 
class Trie:
    # ...

    def contains(self, word):
        node = self
        for char in word:
            if char in node.children:
                node = node.children[char]
            else:
                return False
        return node.end
PHP 
<?php
class Trie
{
    //...
    public function contains($word) {
        $node = $this;
        for ($i = 0; $i < strlen($word); $i++) {
            $char = $word[$i];
            if (isset($node->children[$char])) {
                $node = $node->children[$char];
            } else {
                return false;
            }
        }
        return $node->end;
    }
}

Вставка слова

В таком случае операция вcтавки слова в дерево будет выглядеть следующим образом:

class Trie {
  //...
    insert(word) {
        let node = this;
        for (let i = 0; i < word.length; i++) {
            if (!node.children[word[i]]) {
                node.children[word[i]] = new Trie(word[i], node);
            }
            node = node.children[word[i]];
            if (i === word.length - 1) {
                node.end = true;
            }
        }
    }
}
Java 
class Trie {
    //...
    public void insert(String word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            char ch = word.charAt(i);
            if (!node.children.containsKey(ch)) {
                node.children.put(ch, new Trie(ch, node));
            }
            node = node.children.get(ch);
            if (i == word.length() - 1) {
                node.end = true;
            }
        }
    }
}
Python 
class Trie:
    # ...

    def insert(self, word):
        node = self
        for char in word:
            if char not in node.children:
                node.children[char] = Trie(char, node)
            node = node.children[char]
        node.end = True
PHP 
<?php
class Trie
{
    //...
    public function insert($word) {
        $node = $this;
        for ($i = 0; $i < strlen($word); $i++) {
            $char = $word[$i];
            if (!isset($node->children[$char])) {
                $node->children[$char] = new Trie($char, $node);
            }
            $node = $node->children[$char];
            if ($i === strlen($word) - 1) {
                $node->end = true;
            }
        }
    }
}

Удаление слова

Операция удаления слова принимает следующий вид:

class Trie {
  //...

  remove(word) {
        let node = this;
        const findWord = (node, word, index) => {
            if (index === word.length) {
                if (!node.end) {
                    return false;
                }
                node.end = false;
                return Object.keys(node.children).length === 0;
            }
            if (findWord(node.children[word[index]], word, index + 1)) {
                delete node.children[word[index]];
                return !node.end && Object.keys(node.children).length === 0;
            }
            return false;
        };
        findWord(node, word, 0);
    }
}

https://replit.com/@hexlet/algorithms-trees-prefix-js#index.js

Java 
class Trie {
    //...

    public void remove(String word) {
        Trie node = this;
        removeWord(node, word, 0);
    }

    private boolean removeWord(Trie node, String word, int index) {
        if (index == word.length()) {
            if (!node.end) {
                return false;
            }
            node.end = false;
            if (node.children.isEmpty()) {
                node.parent.children.remove(word.charAt(index - 1));
            }
            return true;
        }
        char ch = word.charAt(index);
        if (removeWord(node.children.get(ch), word, index + 1)) {
            node.children.remove(ch);
            return !node.end && node.children.isEmpty();
        }
        return false;
    }
}

https://replit.com/@hexlet/algorithms-trees-prefix-java#src/main/java/Trie.java

Python 
class Trie:
    # ...

    def remove(self, word):
        node = self
        def find_word(node, word, index):
            if index == len(word):
                if not node.end:
                    return False
                node.end = False
                return len(node.children) == 0
            if find_word(node.children[word[index]], word, index + 1):
                del node.children[word[index]]
                return not node.end and len(node.children) == 0
            return False
        find_word(node, word, 0)

https://replit.com/@hexlet/algorithms-trees-prefix-python#main.py

PHP 
<?php
class Trie
{
    //...

    public function remove($word) {
        $node = $this;
        $findWord = function ($node, $word, $index) use (&$findWord) {
            if ($index === strlen($word)) {
                if (!$node->end) {
                    return false;
                }
                $node->end = false;
                if (empty($node->children)) {
                    $node->parent->children = [];
                }
                return true;
            }
            if ($findWord($node->children[$word[$index]], $word, $index + 1)) {
                unset($node->children[$word[$index]]);
                return !$node->end && empty($node->children);
            }
            return false;
        };
        $findWord($node, $word, 0);
    }
}

https://replit.com/@hexlet/algorithms-trees-prefix-php#main.php

Сжатые префиксные деревья

Это особый подвид префиксных деревьев, заслуживающий отдельного внимания.

В таких деревьях мы сжимаем структуру за счет размещения в вершине не одной буквы, а сразу целого фрагмента префикса. При этом из каждого элемента этого префикса существует строго одна связь с другим элементом префикса.

Такие деревья гораздо удобнее использовать для чтения информации за счет уменьшения количества переходов по ссылкам между вершинами.

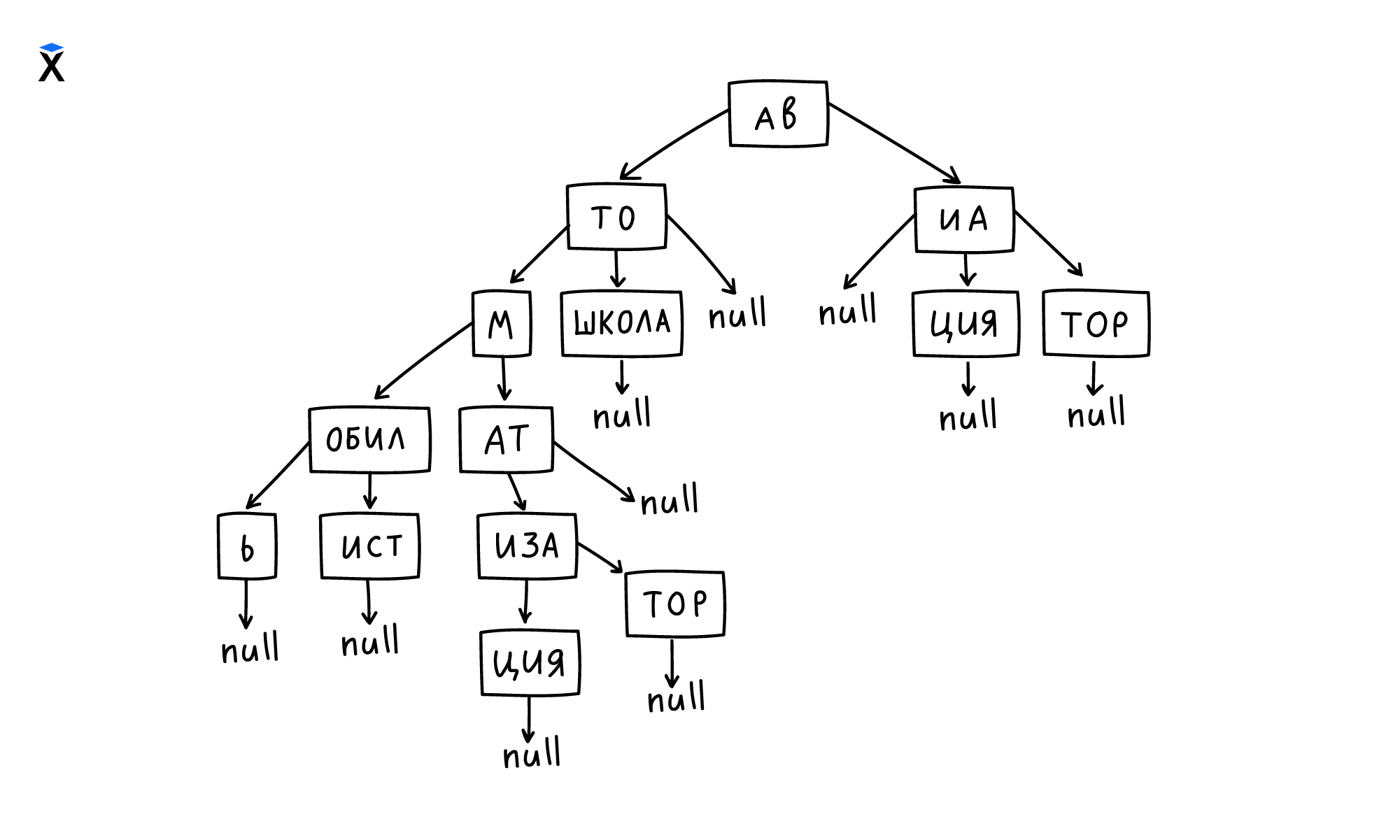
Рассмотрим пример такого дерева на рисунке ниже:

Сжатое префиксное дерево

А так это дерево выглядит без сжатия:

Префиксное дерево

Как видите, количество переходов между вершинами действительно сокращается. Но важно помнить, что такой способ хранения требует более сложную организацию процедур. При сжатии вставка и удаление слов могут потребовать более неочевидной организации вершин — например, их дополнительного разбиения или объединения.

Сжатые префиксные деревья отлично подходят для хранения данных, которые редко подвергаются изменениям.

Выводы

В этом уроке вы познакомились с классическими и сжатыми префиксными деревьями. Это отличный механизм организации хранения группируемых данных. Такой способ хранения уменьшает объем хранимых данных, помогает предсказывать пользовательский ввод, автоматически исправлять ошибки и организовывать маршрутизацию в вычислительных сетях.

Аватары экспертов Хекслета

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты

Об обучении на Хекслете

Для полного доступа к курсу нужен базовый план

Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.

Получить доступ
130
курсов
1000
упражнений
2000+
часов теории
3200
тестов

Открыть доступ

Курсы программирования для новичков и опытных разработчиков. Начните обучение бесплатно

  • 130 курсов, 2000+ часов теории
  • 1000 практических заданий в браузере
  • 360 000 студентов
Отправляя форму, вы принимаете «Соглашение об обработке персональных данных» и условия «Оферты», а также соглашаетесь с «Условиями использования»

Наши выпускники работают в компаниях:

Логотип компании Альфа Банк
Логотип компании Aviasales
Логотип компании Yandex
Логотип компании Tinkoff

Используйте Хекслет по-максимуму!

  • Задавайте вопросы по уроку
  • Проверяйте знания в квизах
  • Проходите практику прямо в браузере
  • Отслеживайте свой прогресс

Зарегистрируйтесь или войдите в свой аккаунт

Отправляя форму, вы принимаете «Соглашение об обработке персональных данных» и условия «Оферты», а также соглашаетесь с «Условиями использования»
Изображение Тото

Задавайте вопросы, если хотите обсудить теорию или упражнения. Команда поддержки Хекслета и опытные участники сообщества помогут найти ответы и решить задачу