Рекурсия — Основы алгоритмов и структур данных

Что такое рекурсия
Рекурсия вместо цикла
Рекурсивный алгоритм для Ханойской башни
Достоинства и недостатки рекурсии
Выводы

В сообществе программистов рекурсия считается не самой простой, но важной темой. Несмотря на сложность, мы решили включить ее в курс по алгоритмам для начинающих.

В этом уроке мы изучим рекурсию, потому что эти знания помогут быстрее и глубже понять алгоритмы. Более того, некоторые важные алгоритмы вообще не получится реализовать без рекурсии.

Что такое рекурсия

Рекурсия — это вызов функции из этой же самой функции. Такое определение может показаться и простым, и непонятным одновременно. Чтобы стало понятнее, посмотрим на такую, самую простую рекурсивную функцию:

const f = () => {
  f();
};

Python

def function():
    function()

PHP

<?php

function f()
{
    f();
}

Java

class App {
    public static void f() {
        f();
    }
}

Этот вызов будет выполняться бесконечно. Кажется, что в этом нет никакого смысла, но это не так — мы докажем это на примере. Попробуем решить такую задачу: посчитать сумму чисел от 1 до 100.

Представим, что мы уже знаем сумму чисел от 1 до 99. Тогда надо просто прибавить к ней 100:

sum(100) = 100 + sum(99)

А если мы не знаем сумму чисел от 1 до 99? Тогда нужно вычислить ее, сложив 99 и сумму чисел от 1 до 98:

sum(99) = 99 + sum(98)

По такой же логике мы будем продвигаться еще много раз. В итоге мы увидим, что программу можно свести к решению такой же задачи, но с меньшим параметром:

const sum = (n) => {
  return n + sum(n - 1);
};

Python

def sum(n):
    return n + sum(n - 1)

PHP

<?php

function sum($n)
{
    return $n + sum($n - 1)
}

Java

class App {
    public static int sum(int n) {
        return n + sum(n - 1);
    }
}

У нас получилась рекурсивная функция. В таком виде она будет работать бесконечно: сначала параметр n уменьшается до 0, потом становится равным -1, -2 и так далее.

Нужно придумать, как остановить бесконечный вызов. Напишем код, который остановит функцию тогда, когда она дойдет до единицы. Это кажется логичным несмотря на то, что мы не можем подсчитать сумму чисел от 1 до 1. Мы берем число 1, и ни с чем его не складываем:

sum(1) = 1

У нас получается рекурсивная функция sum:

const sum = (n) => {
  if (n === 1) {
    return 1;
  }

  return n + sum(n - 1);
};

sum(100) // 5050

https://replit.com/@hexlet/js-recursion-sum

Python

def sum(n):
    if n == 1:
        return 1

    return n + sum(n - 1)

sum(100) # 5050

https://replit.com/@hexlet/python-reccursion-sum#main.py

PHP

<?php

function sum($n)
{
    if ($n === 1) {
      return 1;
    }

    return $n + sum($n - 1);
};

sum(100); //  5050

https://replit.com/@hexlet/php-reccursion-sum#main.php

Java

class App {
    public static int sum(int n) {
        if (n == 1) {
            return 1;
        }

        return n + sum(n - 1);
    }
}

App.sum(100); // 5050

https://replit.com/@hexlet/java-reccursion-sum#src/main/java/Main.java

Теперь рекурсивная функция остановится после ста вызовов и вычислит сумму чисел от 1 до 100.

Мы видим, что рекурсивные функции выглядят достаточно просто и делают то, что нам надо. Но пример выше не раскрыл весь потенциал рекурсии, а ведь она полезна для множества других задач. Изучим еще несколько примеров и посмотрим, где еще пригождаются знания о рекурсии.

Рекурсия вместо цикла

Один из распространенных алгоритмов в программировании — это бинарный поиск, который мы уже изучали в этом курсе. Мы уже рассмотрели его реализацию через циклы:

const binarySearch = (items, value) => {
  let left = 0;
  let right = items.length - 1;

  while (left <= right) {
    const middle = Math.floor((left + right) / 2);

    if (value == items[middle]) {
      return middle;
    }

    if (value < items[middle]) {
      right = middle - 1;
    } else {
      left = middle + 1;
    }
  }

  return -1;
};

const items = [-3, -1, 1, 3, 5, 7, 9, 11];
console.log(binarySearch(items, 100)); // => -1
console.log(binarySearch(items, -1)); // => 1
console.log(binarySearch(items, 7)); // => 5

Python

def binary_search(items, value):
    left = 0
    right = len(items) - 1

    while (left <= right):
        middle = (left + right) // 2

        if value == items[middle]:
            return middle

        if value < items[middle]:
            right = middle - 1
        else:
            left = middle + 1

    return -1


items = [-3, -1, 1, 3, 5, 7, 9, 11]
print(binary_search(items, 100))  # => -1
print(binary_search(items, -1))  # => 1
print(binary_search(items, 7))  # => 5

PHP

<?php

function binarySearch($items, $value)
{
    $left = 0;
    $right = count($items) - 1;

    while ($left <= $right) {
        $middle = round(($left + $right) / 2);

        if ($value === $items[$middle]) {
           return $middle;
        }

        if ($value < $items[$middle]) {
              $right = $middle - 1;
        } else {
              $left = $middle + 1;
        }
    }

    $return -1;
}

$items = [-3, -1, 1, 3, 5, 7, 9, 11];
print_r(binarySearch($items, 100)); // => -1
print_r(binarySearch($items, -1)); // => 1
print_r(binarySearch($items, 7)); // => 5

Java

class App {
    public static int binarySearch(List<Integer> items, int value) {
        var left = 0;
        var right = items.size() - 1;

        while (left <= right) {
            var middle = (left + right) / 2;

            if (value == items.get(middle)) {
                return middle;
            }

            if (value < items.get(middle)) {
                right = middle - 1;
            } else {
                left = middle + 1;
            }
        }

        return -1;
    }
}

List<Integer> items = List.of(-3, -1, 1, 3, 5, 7, 9, 11);
App.binarySearch(items, 100); // -1
App.binarySearch(items, -1); // 1
App.binarySearch(items, 7); // 5

Тогда мы описывали алгоритм через циклы, поэтому объяснение было подробным и сложным. Алгоритм бинарного поиска можно описать намного проще, если опираться на знания о рекурсии:

Если массив пустой, то поиск завершается неудачно
Если массив не пустой, сравниваем наш элемент со средним элементом массива. Если они равны, поиск завершается удачно
Если средний элемент больше нужного, повторяем поиск в левой половине массива
Если средний элемент меньше нужного, повторяем поиск в правой половине массива

И это все: мы свели задачу поиска к самой себе. Сначала зона поиска — это весь массив, но на каждом шаге она сужается в два раза. Если нужного элемента в массиве не окажется, зона поиска сузится до пустого массива, и поиск завершится неудачно:

const binarySearch = (items, value, left, right) => {
  if (left > right) {
    return -1;
  }

  const middle = Math.floor((left + right) / 2);
  if (value == items[middle]) {
    return middle;
  }

  if (value < items[middle]) {
    return binarySearch(items, value, left, middle - 1);
  }

  return binarySearch(items, value, middle + 1, right);
};

const items = [-3, -1, 1, 3, 5, 7, 9, 11];
console.log(binarySearch(items, 100, 0, items.length - 1)); // => -1
console.log(binarySearch(items, -1, 0, items.length - 1)); // => 1
console.log(binarySearch(items, 7, 0, items.length - 1)); // => 5

https://replit.com/@hexlet/js-reccursion-binary-search#index.js

Python

def binary_search(items, value, left, right):
    if left > right:
        return -1

    middle = (left + right) // 2

    if value == items[middle]:
        return middle

    if value < items[middle]:
        return binary_search(items, value, left, middle - 1)

    return binary_search(items, value, middle + 1, right)


items = [-3, -1, 1, 3, 5, 7, 9, 11]
print(binary_search(items, 100, 0, len(items) - 1))  # => -1
print(binary_search(items, -1, 0, len(items) - 1))  # => 1
print(binary_search(items, 7, 0, len(items) - 1))  # => 5

https://replit.com/@hexlet/python-reccursion-binary-search#main.py

PHP

<?php

function binarySearch($items, $value, $left, $right)
{
    if ($left > $right) {
       return -1;
    }

    $middle = round(($left + $right) / 2);
    if ($value === $items[$middle]) {
        return $middle;
    }

    if ($value < $items[$middle]) {
        return binarySearch($items, $value, $left, $middle - 1);
    }

      return binarySearch($items, $value, $middle + 1, $right);
}

$items = [-3, -1, 1, 3, 5, 7, 9, 11];
print_r(binarySearch($items, 100, 0, count($items) - 1)); // => -1
print_r(binarySearch($items, -1, 0, count($items) - 1)); // => 1
print_r(binarySearch($items, 7, 0, count($items) - 1)); // => 5

https://replit.com/@hexlet/php-reccursion-binary-search#main.php

Java

class App {
    public static int binarySearch(List<Integer> items, int value, int left, int right) {
        if (left > right) {
            return -1;
        }

        var middle = (left + right) / 2;

        if (value == items.get(middle)) {
            return middle;
        }

        if (value < items.get(middle)) {
            return binarySearch(items, value, left, middle - 1);
        }

        return binarySearch(items, value, middle + 1, right);
    }
}

List<Integer> items = List.of(-3, -1, 1, 3, 5, 7, 9, 11);
App.binarySearch(items, 100, 0, items.size() - 1); // -1
App.binarySearch(items, -1, 0, items.size() - 1); // 1
App.binarySearch(items, 7, 0, items.size() - 1); // 5

https://replit.com/@hexlet/java-reccursion-binary-search#src/main/java/Main.java

https://replit.com/@hexlet/algorithms-recursion

Как видно на примере выше, рекурсивный алгоритм очень похож на итерационный — то есть сделанный с помощью цикла. Но его гораздо проще объяснять не через циклы, а через рекурсию.

Продолжим изучать рекурсию на еще одном примере.

Рекурсивный алгоритм для Ханойской башни

eyJpZCI6ImI4YTFiOThjOTUzYzEzZDIxMzcyZTcyODA2MTBmOWZhLmpwZyIsInN0b3JhZ2UiOiJjYWNoZSJ9?signature=413897c55a90931603f0c5eb595b91d11a2e62e02bbf5081a791dbbf4e8134da

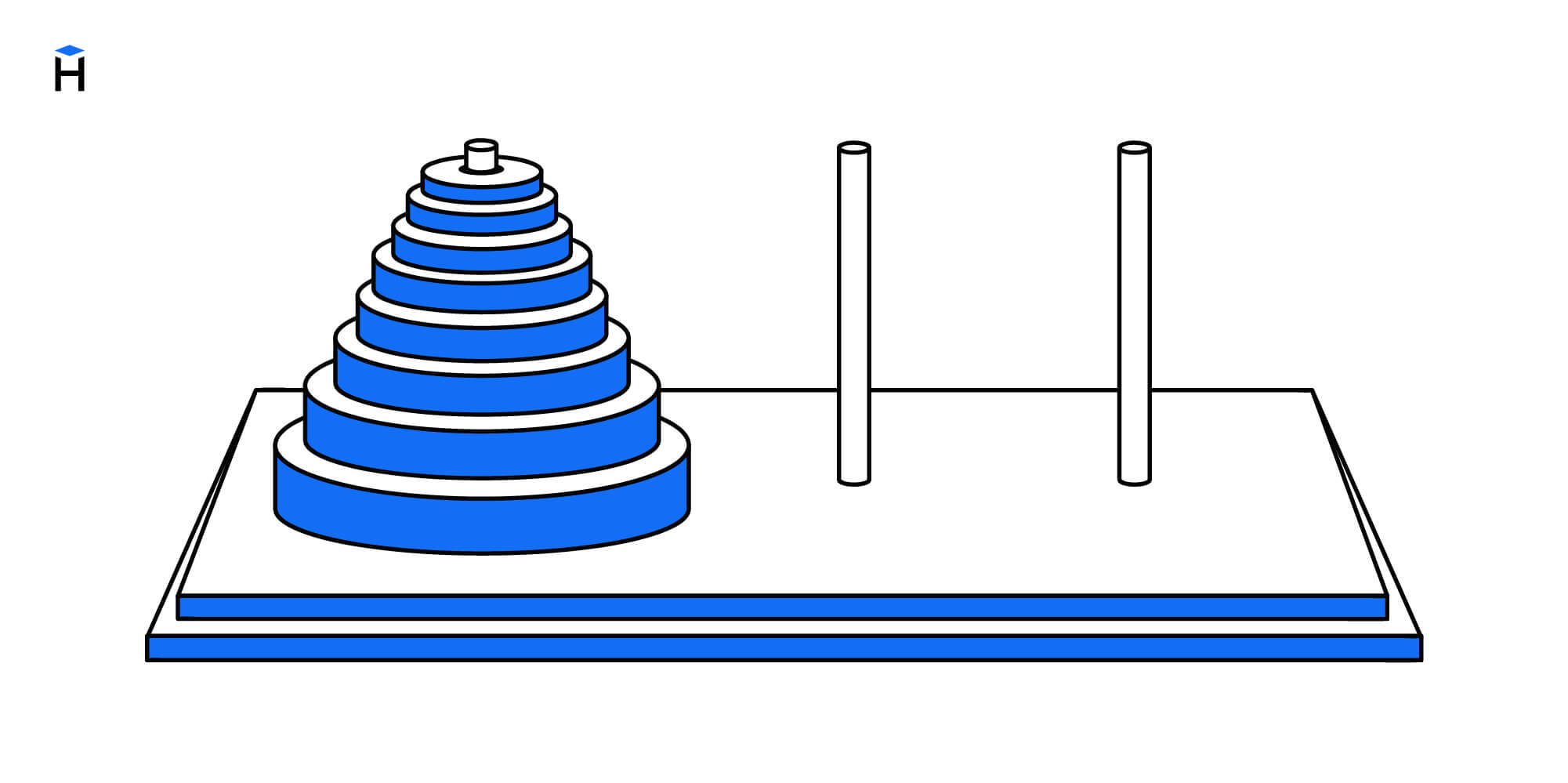
Ханойская башня — это знаменитая древняя головоломка. Она состоит из трех стержней, на один из которых надеты кольца разного размера.

Надо перенести все кольца на другой стержень, при этом кольца можно переносить только по одному. Главное правило: никогда нельзя класть кольцо большего размера на кольцо меньшего.

Попробуем спроектировать алгоритм, который решит эту головоломку. Для начала формализуем задачу:

Обозначим стержни числами 1, 2 и 3
Определимся, что нам нужен универсальный алгоритм, который решает головоломку при любой высоте башен
Назовем функцию hanoi и зададим ей три параметра:
1. Количество колец (высота башни, которую мы хотим перенести)
2. Номер стержня, откуда мы будем переносить башню
3. Номер стержня, куда мы будем переносить башню

Таким образом, вызов hanoi(10, 1, 3) будет означать: «Перенести башню из десяти колец с первого стержня на третий».

Функция должна печатать последовательность переносов: взять верхнее кольцо со стержня №1 и перенести его на стержень №2. Мы не можем взять второе сверху кольцо или пятое сверху — только самое верхнее. Поэтому нам достаточно просто выводить номера обоих стержней: откуда снимать кольцо и куда переносить.

Если оставить все как есть, мы столкнемся с такой проблемой: можно перенести первые два кольца, но третье кольцо переместить не получится, потому что оно больше обоих колец на соседних стержнях. Как быть?

Здесь на помощь приходит рекурсия. Попробуем упростить задачу и свести ее к самой себе:

Предположим, что мы уже умеем переносить башню из четырех колец
Дальше нам надо перенести башню из пяти с первого стержня на второй
Воспользуемся третьим стержнем и перенесем на него четыре верхних кольца
Теперь можем взять самое большое кольцо с первого стержня и перенести его на пустой второй
Осталось снять башню из четырех колец со вспомогательного третьего стержня и перенести ее на второй стержень, на котором уже лежит большое пятое кольцо второго стержня — это мы уже умеем

Можно ли будет класть какие-то кольца поверх самого большого пятого? Да, потому что правила запрещают только класть большие кольца на меньше, а наоборот — нет. Оказывается, что этих рассуждений достаточно, чтобы написать рекурсивную функцию.

Только мы знаем, что рекурсия должна где-то останавливаться. В нашем случае минимальная задача, которую мы можем решить — перенос башни из одного кольца. Она решается тривиально: одно кольцо мы можем перенести безо всяких условий, поэтому нам достаточно просто вывести номера стержней «откуда» и «куда»:

const hanoi = (height, from, to) => {
  if (height === 1) {
    console.log("с %d на %d", from, to);
    return;
  }

  const temporary = 6 - from - to;
  hanoi(height - 1, from, temporary);
  console.log("с %d на %d", from, to);
  hanoi(height - 1, temporary, to);
};

hanoi(4, 1, 2);
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2
// => с 1 на 3
// => с 2 на 1
// => с 2 на 3
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2
// => с 3 на 1
// => с 2 на 1
// => с 3 на 2
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2

https://replit.com/@hexlet/hanoi

Python

def hanoi(height, start, to):
    if height == 1:
        print(f'с {start} на {to}')
        return

    temporary = 6 - start - to
    hanoi(height - 1, start, temporary)
    print(f'с {start} на {to}')
    hanoi(height - 1, temporary, to)

hanoi(4, 1, 2)
# => с 1 на 3
# => с 1 на 2
# => с 3 на 2
# => с 1 на 3
# => с 2 на 1
# => с 2 на 3
# => с 1 на 3
# => с 1 на 2
# => с 3 на 2
# => с 3 на 1
# => с 2 на 1
# => с 3 на 2
# => с 1 на 3
# => с 1 на 2
# => с 3 на 2

https://replit.com/@hexlet/python-reccursion-hanoi#main.py

PHP

<?php

function hanoi($height, $from, $to)
{
    if ($height === 1) {
        print_r("с {$from} на {$to}\n");
        return;
    }

    $temporary = 6 - $from - $to;
    hanoi($height - 1, $from, $temporary);
    print_r("с {$from} на {$to}\n");
    hanoi($height - 1, $temporary, $to);
}

hanoi(4, 1, 2);
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2
// => с 1 на 3
// => с 2 на 1
// => с 2 на 3
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2
// => с 3 на 1
// => с 2 на 1
// => с 3 на 2
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2

https://replit.com/@hexlet/php-reccursion-hanoi#main.php

Java

class App {
    public static void hanoi(int height, int from, int to) {
        if (height == 1) {
            System.out.println(String.format("с %d на %d", from, to));
            return;
        }

        var temporary = 6 - from - to;
        hanoi(height - 1, from, temporary);
        System.out.println(String.format("с %d на %d", from, to));
        hanoi(height - 1, temporary, to);
    }
}

App.hanoi(4, 1, 2);
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2
// => с 1 на 3
// => с 2 на 1
// => с 2 на 3
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2
// => с 3 на 1
// => с 2 на 1
// => с 3 на 2
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2

https://replit.com/@hexlet/java-reccursion-hanoi#src/main/java/Main.java

Удивительно, что этот алгоритм казался сложным на словах, но в коде получился таким простым. Здесь мы применили один трюк, который помогает упростить код. Разберем его подробнее.

Во время работы алгоритма стержни постоянно меняются ролями. Например, если мы хотим перенести башню с первого стержня на третий, то второй стержень выступает как вспомогательный — туда мы перенесем все кольца, кроме нижнего. А если мы переносим маленькую башню с первого стержня на второй, то роль вспомогательного переходит третьему стержню.

Чтобы определить номер вспомогательного стержня, надо написать сложное условие:

if (from === 1 && to === 2 || from === 2 && to === 1) {
  temporary = 3;
} else if (from === 2 && to === 3 || from === 3 && to === 2) {
  temporary = 1;
} else if (from === 1 && to === 3 || from === 3 && to === 1) {
  temporary = 2;
}

Python

if (start == 1 and to == 2) or (start == 2 and to == 1):
    temporary = 3
elif (start == 2 and to == 3) or (start == 3 and to == 2):
    temporary = 1
elif (start == 1 and to == 3) or (start == 3 and to == 1):
    temporary = 2

PHP

<?php

if ($from === 1 && $to === 2 || $from === 2 && $to === 1) {
    $temporary = 3;
} else if ($from === 2 && $to === 3 || $from === 3 && $to === 2) {
    $temporary = 1;
} else if ($from === 1 && $to === 3 || $from === 3 && $to === 1) {
    $temporary = 2;
}

Java

if (from == 1 && to == 2 || from == 2 && to == 1) {
    temporary = 3;
} else if (from == 2 && to == 3 || from == 3 && to == 2) {
    temporary = 1;
} else if (from == 1 && to == 3 || from == 3 && to == 1) {
    temporary = 2;
}

Несмотря на то, что логика этого кода понятна, само условие выглядит громоздким. Разберем по шагам, как оно работает. В коде используют три константы:

from — номер стержня, с которого мы перемещаем кольца
to — номер стержня, на который мы хотим переместить наши кольца
temporary — номер стержня, который мы используем для временного хранения первых n-1 дисков

Еще в вызове указано количество колец — высота башни, которую мы хотим перенести. Таким образом, вызов hanoi(n, 1, 3) будет означать: «Перенести башню из n колец с первого стержня на третий».

Обратите внимание, что сумма from, to и temporary всегда равна 6. Можно взять число 6 и вычесть из него номера стержней from и to, и тогда мы узнаем номер вспомогательного стержня:

const temporary = 6 - from - to;

Python

temporary = 6 - start - to

PHP

<?php

$temporary = 6 - $start - $to;

Java

var temporary = 6 - from - to;

Этот код гораздо проще, но требует разъяснений. В начале каждой рекурсивной функции мы должны проверить граничное условие — оно помогает не войти в бесконечный вызов. В задаче о ханойской башне граничное условие — это башня из одного кольца.

Если встретилась такая башня, надо перенести кольцо и завершить работу:

if (height === 1) {
  console.log("с %d на %d", from, to);
  return;
}

Python

if height == 1:
    print(f'с {start} на {to}')
    return

PHP

<?php

if ($height === 1) {
    print_r("с {$from} на {$to}");
    return;
}

Java

if (height == 1) {
    System.out.println(String.format("с %d на %d", from, to));
    return;
}

Если высота башни height больше единицы, мы упрощаем задачу и сводим ее к самой себе. В случае ханойской башни такая задача — перенести башни высотой height - 1 на вспомогательный стержень. После этого можно перенести самое большое кольцо на стержень «куда», а потом — переместить на него маленькую башню со вспомогательного стержня:

hanoi(height - 1, from, temporary);
console.log("с %d на %d", from, to);
hanoi(height - 1, temporary, to);

Python

hanoi(height - 1, start, temporary)
print(f'с {start} на {to}');
hanoi(height - 1, temporary, to)

PHP

<?php

hanoi($height - 1, $from, $temporary);
print_r("с {$from} на {$to}");
hanoi($height - 1, $temporary, $to);

Java

hanoi(height - 1, from, temporary);
System.out.println(String.format("с %d на %d", from, to));
hanoi(height - 1, temporary, to);

Достоинства и недостатки рекурсии

Чтобы начать понимать рекурсивный код, программист должен к нему привыкнуть и самостоятельно разобрать или решить несколько рекурсивных задач. Со временем оказывается, что рекурсивный код очень простой и короткий. Поэтому простоту кода относят к плюсам рекурсии.

Еще один плюс — знания о рекурсии открывают программисту новые возможности. Многие задачи можно решить и с помощью циклов, но есть и те, в которых не обойтись без рекурсии. Например, синтаксический разбор арифметических выражений можно сделать только рекурсивно. Вот так выглядит сложное арифметическое выражение, если решать его через рекурсивный алгоритм:

sin(a) + (3 + 2 * b ** 7 - cos (a / b))

К недостаткам рекурсивных решений относят потребление памяти. При каждом вызове функции компьютер тратит память на передачу параметров, а также сохраняет адрес следующей инструкции — чтобы понимать, откуда продолжить выполнение программы, когда функция завершится. Большое количество рекурсивных вызовов может привести к исчерпанию памяти.

Компьютер сохраняет данные в специальной области, которая называется стек. Когда вся память исчерпана, возникает ошибка переполнения стека. По-английски эта ошибка называется stack overflow. В честь этой ошибки назван сайт stackoverflow.com, где программисты отвечают на вопросы друг друга об ошибках в их программах.

В любом языке программирования может произойти переполнение стека. Впрочем, опытные программисты умеют с этим справляться, а вот для новичков эта тема не так очевидна. Считается, что переполнение стека — одна из самых частых ошибок начинающих программистов, когда они осваивают рекурсию.

Выводы

Рекурсия — важный прием в программировании. Она используется при проектировании алгоритмов и помогает решать задачи, которые невозможно решить другим способом
Рекурсию можно использовать вместо циклов (итераций). Часто рекурсивные программы короче и понятнее итеративных
Иногда рекурсия способна заметно упростить алгоритм, как в нашем примере с Ханойской башней
Рекурсия может привести к переполнению стека, и это самая частая ошибка новичков

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты

Для полного доступа к курсу нужен базовый план

Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.

Получить доступ

130

курсов

1000

упражнений

2000+

часов теории

3200

тестов