Алгоритмы сортировки — Основы алгоритмов и структур данных

Чем полезна сортировка
Три алгоритма сортировки
Пузырьковая сортировка
Сортировка выбором
Быстрая сортировка
- Принцип работы быстрой сортировки
- Как реализовать быструю сортировку
Универсальная функция сортировки

В программировании часто встречаются задачи, которые трудно решить «в лоб». Представим, что нам нужно избавиться от повторяющихся элементов в массиве. Попробуем найти все числа, которые встречаются здесь больше, чем один раз:

7, 3, 1, 9, 10, 2, 3, 6, 9, 4, 7, 5, 5, 4, 2, 8, 4, 7

Чтобы это сделать, нужно написать сложный алгоритм. Можно упростить задачу и отсортировать массив. В нем повторяющиеся элементы находятся рядом, поэтому их легко обнаружить, сравнивая соседние числа:

1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 6, 7, 7, 7, 8, 9, 9, 10

Не удивительно, что одной из самых полезных задач в программировании считается сортировка — перестановка элементов в массиве так, чтобы они располагались в убывающем или возрастающем порядке.

Чем полезна сортировка

Познакомимся с сортировкой поближе и выясним, где она встречается в практических задачах программиста.

Посмотрим на любой интернет-магазин. В каждом разделе встречаются сотни и тысячи товаров, из которых так сложно выбрать подходящий. Чтобы пользователям было удобнее, магазин предлагает сортировку товаров по цене, по рейтингу или по популярности.

При этом покупатели выбирают сортировку по своим целям:

По возрастанию цены в поисках выгодных предложений
По убыванию цены, если готовы на дорогую покупку

Чтобы интернет-магазин умел сортировать одни и те же записи по-разному, необходима универсальная функция сортировки, о которой поговорим в конце урока.

Три алгоритма сортировки

Существуют десятки алгоритмов сортировки, но изучать все слишком долго. Чтобы не останавливаться на этой теме, мы выбрали три фундаментальных алгоритма:

Пузырьковая сортировка
Сортировка выбором
Быстрая сортировка

Все три алгоритма сортируют исходный массив, меняя местами его элементы и не требуя дополнительного пространства.

Эти алгоритмы помогут понять, как работает сортировка. На их примере вы изучите, какие техники программисты применяют при разработке алгоритмов.

При реализации алгоритмов мы должны помнить о вырожденных случаях — массивах, в которых один или ноль элементов. Сортировка их не меняет, но наши алгоритмы должны обрабатывать эти случаи — иначе программа завершится с ошибкой.

Пузырьковая сортировка

Один из самых простых методов — пузырьковая сортировка. Это название произошло от ассоциации с воздухом в воде: на дне пузырьки совсем маленькие, но постепенно поднимаются к поверхности, собирают кислород и увеличиваются.

Похожий принцип работает и с элементами массива при такой сортировке. Посмотрите на этот рисунок:

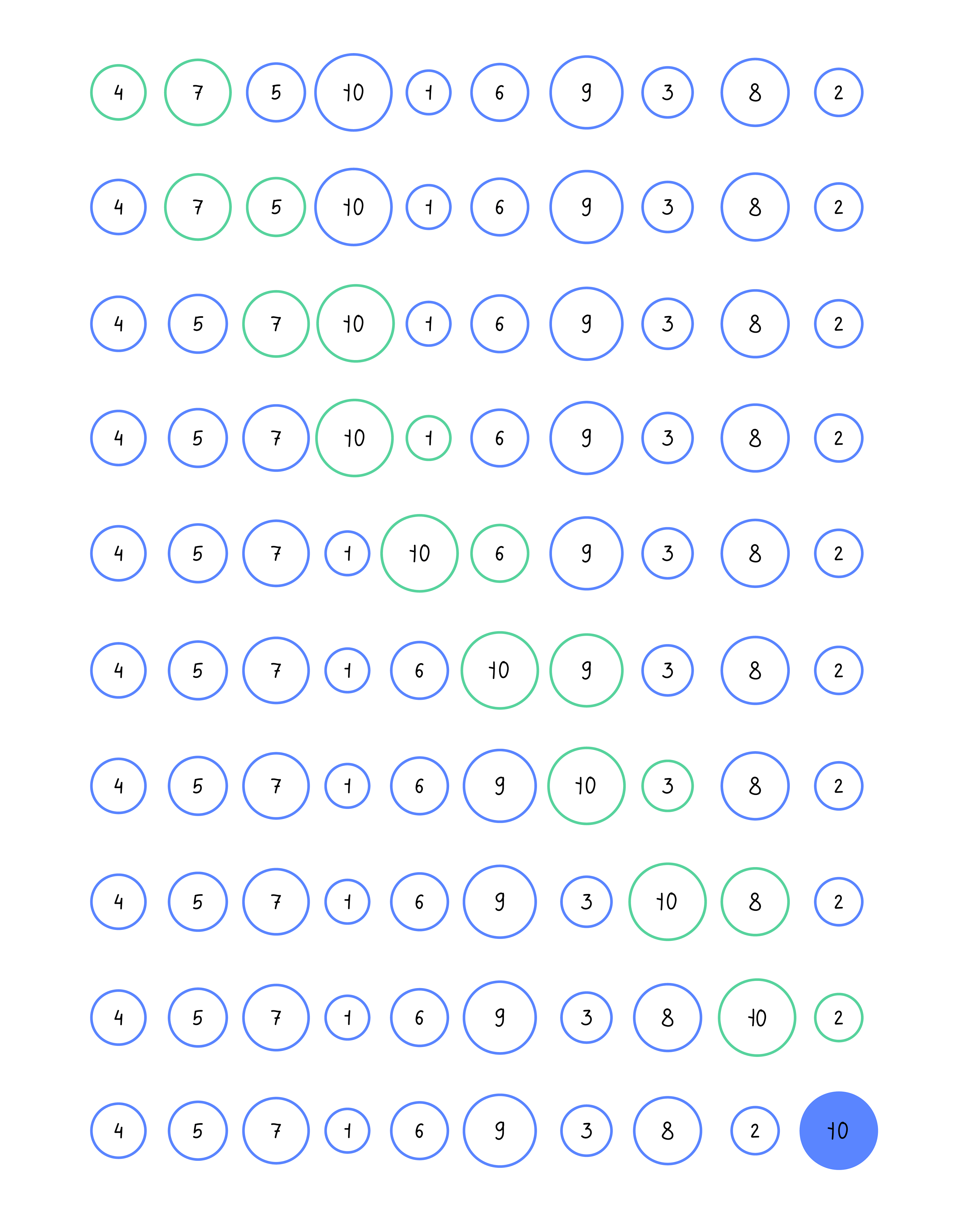
Мы идем по массиву и перемещаем вправо самый большой элемент из просмотренных. Так мы находим элемент со значением 10, который в итоге побеждает во всех сравнениях и оказывается в правом конце массива.

Рассмотрим механизм работы данной сортировки на реальном примере. Возьмем массив и сравним элементы попарно от начала к концу: первый со вторым, второй с третьим, третий с четвертым и так далее.

Если два соседних элемента находятся в неправильном порядке, меняем их местами. После первого прохода самый большой элемент оказывается справа — его можно больше не сравнивать и не перемещать. Далее повторяем те же действия со всеми остальными числами.

Пузырьковая сортировка реализуется в JavaScript с помощью такой функции:

const bubbleSort = (items) => {
  for (let limit = items.length - 1; limit > 0; limit -= 1) {
    for (let i = 0; i < limit; i += 1) {
      if (items[i] > items[i + 1]) {
        const temporary = items[i];
        items[i] = items[i + 1];
        items[i + 1] = temporary;
      }
    }
  }
};

https://replit.com/@hexlet/js-sorting-bubble-sort#index.js

Python

def bubble_sort(items):
    for limit in range(len(items) - 1, 0, -1):
        for i in range(limit):
            if items[i] > items[i + 1]:
                items[i], items[i + 1] = items[i + 1], items[i]

https://replit.com/@hexlet/python-sorting-bubble-sort#main.py

PHP

<?php

function bubbleSort(&$items)
{
    for ($limit = count($items) - 1; $limit > 0; $limit -= 1) {
        for ($i = 0; $i < $limit; $i += 1) {
            if ($items[$i] > $items[$i + 1]) {
                $temporary = $items[$i];
                $items[$i] = $items[$i + 1];
                $items[$i + 1] = $temporary;
            }
        }
    }
}

https://replit.com/@hexlet/php-sorting-bubble-sort#main.php

Java

class App {
    public static void bubbleSort(int[] items) {
        for (var limit = items.length - 1; limit > 0; limit--) {
            for (var i = 0; i < limit; i++) {
                if (items[i] > items[i + 1]) {
                    var temporary = items[i];
                    items[i] = items[i + 1];
                    items[i + 1] = temporary;
                }
            }
        }
    }
}

https://replit.com/@hexlet/java-sorting-bubble-sort#src/main/java/Main.java

Мы видим здесь два вложенных цикла. Внешний цикл ограничивает внутренний цикл на каждом проходе. Сначала он простирается до конца массива, но после первого прохода там оказывается максимальный элемент.

Внутренний цикл на следующем проходе движется до предпоследнего элемента, а затем до пред-пред-последнего — и так до тех пор, пока не остается один элемент в левой части:

for (let limit = items.length - 1; limit > 0; limit -= 1) {
  // ...
}

Python

for limit in range(len(items) - 1, 0, -1):
    # ...

PHP

<?php

for ($limit = count(items) - 1; $limit > 0; $limit -= 1) {
    // ...
}

Java

for (var limit = items.length - 1; limit > 0; limit--) {
    // ...
}

Мы помним, что в JavaScript элементы массива нумеруются с 0 — следовательно, индекс последнего элемента массива items равен items.length - 1.

Обмен двух элементов выполняется с помощью временной переменной, которую мы назвали temporary (т.е. временная):

const temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;

Python

# В Python временная переменная не требуется
items[i], items[i + 1] = items[i + 1], items[i]

PHP

<?php

$temporary = $items[$i];
$items[$i] = $items[$i + 1];
$items[$i + 1] = $temporary;

Java

var temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;

На каждом шаге мы находим наибольший элемент в массиве, а последний оставшийся неизбежно оказывается наименьшим — так мы получаем упорядоченный массив. Проверим работу алгоритма:

const items = [2, 3, 4, 3, 1, 2, 4, 5, 1, 2];
bubbleSort(items);
console.log(items); // => [1, 1, 2, 2, 2, 3, 3, 4, 4, 5]

https://replit.com/@hexlet/js-sorting-bubble-sort#index.js

Python

items = [2, 3, 4, 3, 1, 2, 4, 5, 1, 2]
bubble_sort(items)
print(items)  # => [1, 1, 2, 2, 2, 3, 3, 4, 4, 5]

https://replit.com/@hexlet/python-sorting-bubble-sort#main.py

PHP

<?php

$items = [2, 3, 4, 3, 1, 2, 4, 5, 1, 2];
bubbleSort($items);
print_r($items); // => [1, 1, 2, 2, 2, 3, 3, 4, 4, 5]

https://replit.com/@hexlet/php-sorting-bubble-sort#main.php

Java

int[] items = {2, 3, 4, 3, 1, 2, 4, 5, 1, 2};
App.bubbleSort(items);
System.out.println(Arrays.toString(items));
// => [1, 1, 2, 2, 2, 3, 3, 4, 4, 5]

https://replit.com/@hexlet/java-sorting-bubble-sort#src/main/java/Main.java

При пузырьковой сортировке соседние элементы часто меняются местами, поэтому она работает довольно медленно. Чтобы сэкономить время, можно сократить количество перестановок. В этом поможет сортировка выбором.

Сортировка выбором

Этот алгоритм сначала проводит операции сравнения и находит наименьший элемент, а только потом помещает его в начало массива. После первого прохода алгоритм исключает первый элемент из рассмотрения и ищет минимальный элемент в оставшейся части массива, а затем помещаем его на второе место:

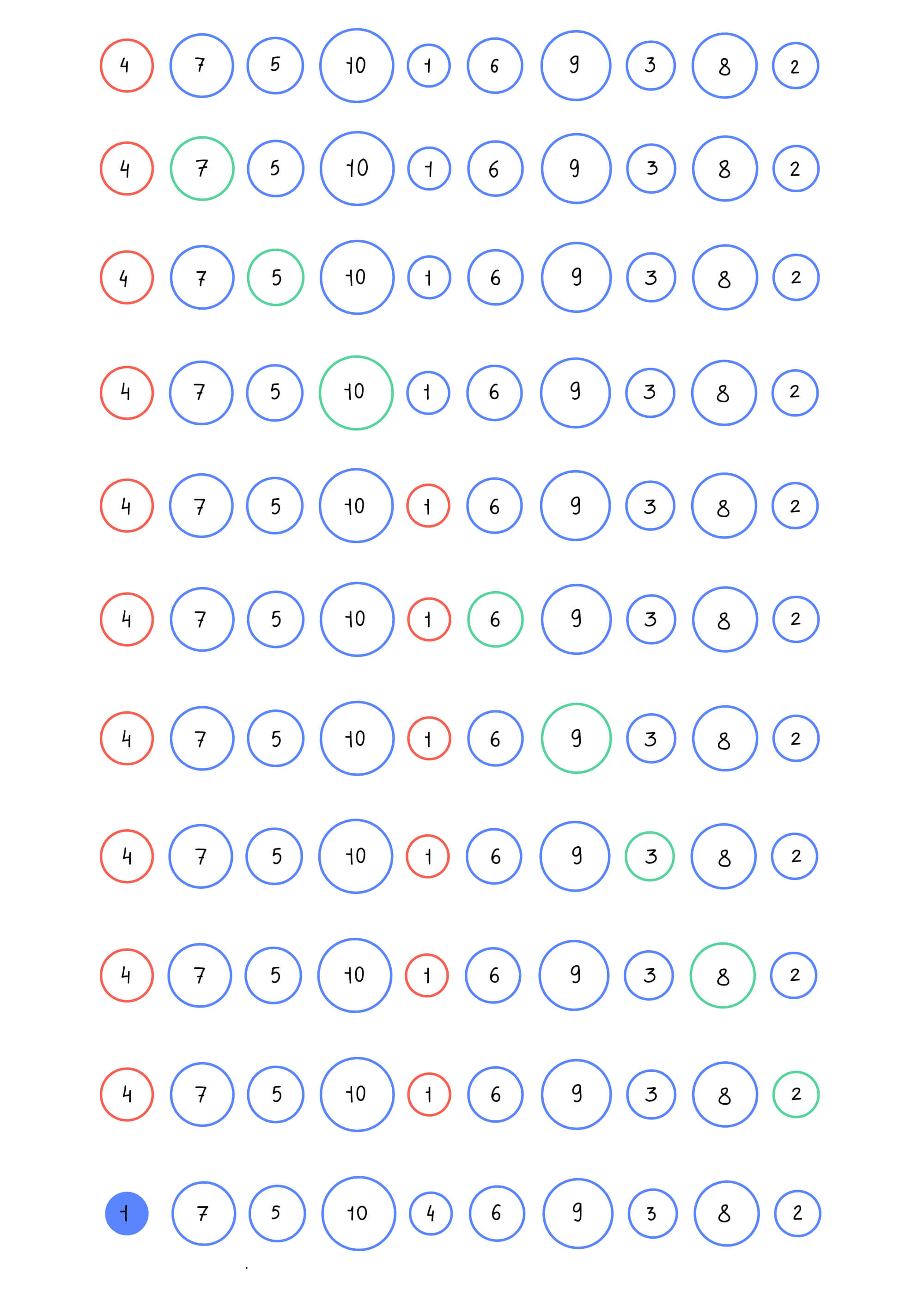
Этот алгоритм работает гораздо быстрее пузырьковой сортировки, потому что сравнений здесь столько же, а вот обмен всего один — в самом конце.

Рассмотрим функцию, реализующую сортировку выбором в Java Script:

const selectionSort = (items) => {
  for (let i = 0; i < items.length - 1; i += 1) {
    let indexMin = i;
    for (let j = i + 1; j < items.length; j += 1) {
      if (items[j] < items[indexMin]) {
        indexMin = j;
      }
    }

    const temporary = items[i];
    items[i] = items[indexMin];
    items[indexMin] = temporary;
  }
};

https://replit.com/@hexlet/js-sorting-selection#index.js

Python

def selection_sort(items):
    for i in range(len(items) - 1):
        index_min = i
        for j in range(i + 1, len(items)):
            if items[j] < items[index_min]:
                index_min = j
        items[i], items[index_min] = items[index_min], items[i]

https://replit.com/@hexlet/python-sorting-selection#main.py

PHP

<?php

function selectionSort(&$items)
{
    for ($i = 0; $i < count($items) - 1; $i += 1) {
        $indexMin = $i;
        for ($j = $i + 1; $j < count($items); $j += 1) {
            if ($items[$j] < $items[$indexMin]) {
                $indexMin = $j;
            }
        }

        $temporary = $items[$i];
        $items[$i] = $items[$indexMin];
        $items[$indexMin] = $temporary;
    }
}

https://replit.com/@hexlet/php-sorting-selection#main.php

Java

class App {
    public static void selectionSort(int[] items) {
        for (var i = 0; i < items.length - 1; i++) {
            var indexMin = i;
            for (var j = i + 1; j < items.length; j++) {
                if (items[j] < items[indexMin]) {
                    indexMin = j;
                }
            }

            var temporary = items[i];
            items[i] = items[indexMin];
            items[indexMin] = temporary;
        }
    }
}

https://replit.com/@hexlet/java-sorting-selection#src/main/java/Main.java

В реализации мы сохраняем не сам минимальный элемент, а его индекс в массиве. Это нужно потому, что в конце каждого прохода минимальный элемент записывается в начало массива. При этом элемент, который был там до этого, нужно вставить куда-то в неупорядоченную половину — легче всего просто поменять их местами.

Быстрая сортировка

Можно сделать сортировку еще быстрее, если менять местами не соседние элементы, а элементы на самом большом расстоянии друг от друга.

Возьмем для примера массив, отсортированный в порядке убывания — от больших к меньшим. Чтобы разместить элементы в порядке возрастания, надо попарно поменять их местами: первый и последний, потом второй и предпоследний, и так далее, как показано на схеме:

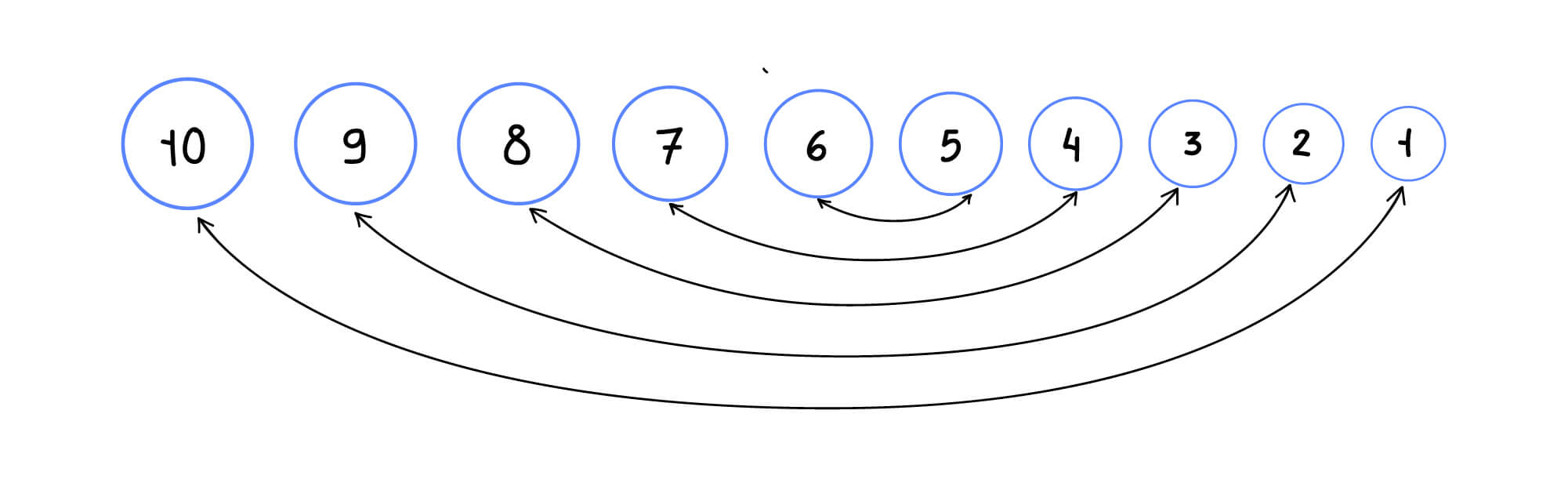
Сортировки массива в обратном порядке реализуется так:

let left = 0;
let right = items.length - 1;

while (left < right) {
  const temporary = items[left];
  items[left] = items[right];
  items[right] = temporary;

  left += 1;
  right -= 1;
}

Python

left = 0
right = len(items) - 1

while left < right:
    items[left], items[right] = items[right], items[left]
    left += 1
    right -= 1

PHP

<?php

$left = 0;
$right = count($items) - 1;

while ($left < $right) {
    $temporary = $items[$left];
    $items[$left] = $items[$right];
    $items[$right] = $temporary;

    $left += 1;
    $right -= 1;
}

Java

var left = 0;
var right = items.length - 1;

while (left < right) {
  var temporary = items[left];
  items[left] = items[right];
  items[right] = temporary;

  left++;
  right--;
}

В примере выше мы создали две переменные-указателя. Переменная left указывает на следующий элемент для обмена слева, а переменная right — справа. Для обмена используем уже знакомую временную переменную temporary:

const temporary = items[left];
items[left] = items[right];
items[right] = temporary;

Python

# В Python временная переменная не требуется
items[left], items[right] = items[right], items[left]

PHP

<?php

$temporary = $items[$left];
$items[$left] = $items[$right];
$items[$right] = $temporary;

Java

var temporary = items[left];
items[left] = items[right];
items[right] = temporary;

На каждой итерации цикла после обмена мы увеличиваем левый указатель, сдвигая его вправо, и одновременно уменьшаем правый, сдвигая влево:

left += 1;
right -= 1;

Python

left += 1
right -= 1

PHP

<?php

$left += 1;
$right -= 1;

Java

left++;
right--;

Похожий подход применяется в алгоритме быстрой сортировки. Он частично упорядочивает массив, перемещая в начало маленькие элементы, а в конец — большие.

Частичное упорядочивание делается с помощью программы, похожей на пример выше. Для начала выбираем опорный элемент — это условный средний элемент, который помогает отличить маленькие элементы от больших. Затем устанавливаем два указателя на начало и конец массива.

Принцип работы быстрой сортировки

Чтобы не запутаться в алгоритме быстрой сортировки, разберем его на схематичном примере. В самом начале наш массив выглядит так:

В качестве опорного элемента выбрано число 4. Левый указатель смотрит на 5, а правый — на 3.

Далее двигаем левый указатель и пропускаем элементы меньше опорного, и ищем неправильный элемент слева. Затем двигаем правый указатель, пропуская элементы больше опорного.

Таким образом мы ищем пару элементов, в которой левый больше правого. Когда пара найдена, меняем элементы местами. В нашем примере 5 и 3 находятся в неправильной позиции — их надо поменять:

Ищем следующую пару для обмена. Справа от 3 находится 4 — наш следующий кандидат для обмена. Обратите внимание, что 4 — опорный элемент, но он тоже принимает участие в сравнениях и обменах.

Слева от числа 5 находятся числа 6, 9 и 7. Они больше опорного элемента 4, поэтому указатель их пропускает. В итоге он останавливается на числе 2:

Меняем их местами и ищем следующую пару. Следующие кандидаты — числа 10 и 1:

Меняем их местами и останавливаемся, потому что левый и правый указатели упираются друг в друга. Мы получили частично упорядоченный массив. Разбиваем его на две части там, где указатели встретились:

Продолжаем частичное упорядочивание левой и правой половин массива. Правая половина перед упорядочиванием показана на рисунке:

Выбираем новый опорный элемент из подмассива. На этот раз это 7. Сдвигая указатели, меняем местами пары 10 и 5, а также 8 и 6. Числа 4 и 9 останутся на своих местах. Частично упорядоченный подмассив принимает такой вид:

Левый и правый указатель встречаются посередине — на числе 7. Мы снова разбиваем массив на две половины и переходим к упорядочиванию левой и правой половин.

Как реализовать быструю сортировку

Попробуем реализовать алгоритм на JavaScript. Начнем с функции частичного упорядочивания:

const partition = (items, left, right, pivot) => {
  while (true) {
    while (items[left] < pivot) {
      left += 1;
    }

    while (items[right] > pivot) {
      right -= 1;
    }

    if (left >= right) {
      return right + 1;
    }

    const temporary = items[left];
    items[left] = items[right];
    items[right] = temporary;

    left += 1;
    right -= 1;
  }
};

Python

def partition(items, left, right, pivot):
    while True:
        while items[left] < pivot:
            left += 1

        while items[right] > pivot:
            right -= 1

        if left >= right:
            return right + 1

        items[left], items[right] = items[right], items[left]
        left += 1
        right -= 1

PHP

<?php

function partition(&$items, $left, $right, $pivot)
{
    while (true) {
        while ($items[$left] < $pivot) {
            $left += 1;
        }

        while ($items[$right] > $pivot) {
            $right -= 1;
        }

        if ($left >= $right) {
            return $right + 1;
        }

        $temporary = $items[$left];
        $items[$left] = $items[$right];
        $items[$right] = temporary;

        $left += 1;
        $right -= 1;
    }
}

Java

class App {
    public static int partition(int[] items, int left, int right, int pivot) {
        while (true) {
            while (items[left] < pivot) {
                left++;
            }

            while (items[right] > pivot) {
                right--;
            }

            if (left >= right) {
                return right + 1;
            }

            var temporary = items[left];
            items[left] = items[right];
            items[right] = temporary;

            left++;
            right--;
        }
    }
}

В качестве параметров функция получает:

Массив items
Указатели на левую и правую часть подмассива left и right
Опорный элемент для сравнения pivot

Сначала в цикле пропускаются элементы слева, которые меньше опорного:

while (items[left] < pivot) {
  left += 1;
}

Python

while items[left] < pivot:
    left += 1

PHP

<?php

while ($items[$left] < $pivot) {
    $left += 1;
}

Java

while (items[left] < pivot) {
    left++;
}

Затем пропускаются элементы справа, которые больше опорного:

while (items[right] > pivot) {
  right -= 1;
}

Python

while items[right] > pivot:
    right -= 1

PHP

<?php

while ($items[$right] > $pivot) {
    $right -= 1;
}

Java

while (items[right] > pivot) {
    right--;
}

Если указатели встретились или зашли друг за друга, мы завершаем цикл и возвращаем место встречи в качестве результата. Нам предстоит разбить массив на два подмассива, поэтому надо решить, что именно возвращать. Мы можем сказать, что граница — это место, где заканчивается левый подмассив, или место, где начинается правый. Большой разницы здесь нет.

Решим, что функция partition возвращает индекс элемента, где начинается правый подмассив:

if (left >= right) {
  return right + 1;
}

Python

if left >= right:
    return right + 1

PHP

<?php

if ($left >= $right) {
    return $right + 1;
}

Java

if (left >= right) {
    return right + 1;
}

Если указатели остановились, то они указывают на два элемента в неверном порядке. Левый указатель смотрит на элемент, который больше опорного. При этом правый указатель смотрит на элемент, который меньше опорного.

Меняем местами и сдвигаем элементы, чтобы в следующей итерации продолжить поиск следующей неправильной пары:

const temporary = items[left];
items[left] = items[right];
items[right] = temporary;

left += 1;
right -= 1;

Python

items[left], items[right] = items[right], items[left]
left += 1
right -= 1

PHP

<?php

$temporary = $items[$left];
$items[$left] = $items[$right];
$items[$right] = $temporary;

$left += 1;
$right -= 1;

Java

var temporary = items[left];
items[left] = items[right];
items[right] = temporary;

Обычно условие завершения цикла пишут в начале (оператор while) или в конце (оператор do…while). В функции partition() условие становится известно в середине цикла.

В языках программирования нет специального синтаксиса для такой ситуации. Обычно программисты записывают бесконечный цикл с помощью конструкции while (true), а выход из цикла делают с помощью операторов break или return:

while (true) {
  // ...

  if (left >= right) {
    return right + 1;
  }

  // ...
}

Python

while True:
    # ...

    if left >= right:
        return right + 1

    # ...

PHP

<?php

while (true) {
    // ...

    if ($left >= $right) {
        return $right + 1;
    }

    // ...
}

Java

while (true) {
    // ...

    if (left >= right) {
        return right + 1;
    }

    // ...
}

Частично упорядоченный массив нельзя назвать полностью отсортированным. Чтобы закончить сортировку, мы должны рекурсивно повторить упорядочивание для левой и правой половин массива.

Про рекурсию мы говорили на прошлом уроке. Так выглядит рекурсивный алгоритм быстрой сортировки. Он немного похож на рекурсивную функцию бинарного поиска:

const sort = (items, left, right) => {
  const length = right - left + 1;

  if (length < 2) {
    return;
  }

  const pivot = items[left];

  const splitIndex = partition(items, left, right, pivot);
  sort(items, left, splitIndex - 1);
  sort(items, splitIndex, right);
};

Python

def sort(items, left, right):
    length = right - left + 1

    if length < 2:
        return

    pivot = items[left]
    split_index = partition(items, left, right, pivot)
    sort(items, left, split_index - 1)
    sort(items, split_index, right)

PHP

<?php

function mySort(&$items, $left, $right)
{
    $length = $right - $left + 1;

    if ($length < 2) {
       return;
    }

    $pivot = $items[$left];

    $splitIndex = partition($items, $left, $right, $pivot);
    mySort($items, $left, $splitIndex - 1);
    mySort($items, $splitIndex, $right);
}

Java

class App {
    public static int partition(int[] items, int left, int right, int pivot) {
        // ...
    }

    public static void sort(int[] items, int left, int right) {
        var length = right - left + 1;

        if (length < 2) {
            return;
        }

        var pivot = items[left];

        var splitIndex = partition(items, left, right, pivot);
        sort(items, left, splitIndex - 1);
        sort(items, splitIndex, right);
    }
}

Для упорядочивания нужно не менее двух элементов. Поэтому мы остановим рекурсивный вызов, когда встретим пустой подмассив или подмассив с одним элементом:

const length = right - left + 1;

if (length < 2) {
  return;
}

Python

length = right - left + 1

if length < 2:
    return

PHP

<?php

$length = $right - $left + 1;

if ($length < 2) {
    return;
}

Java

var length = right - left + 1;

if (length < 2) {
    return;
}

Функция partition возвращает индекс первого элемента в правом подмассиве. Это помогает функции sort корректно вызвать саму себя:

const splitIndex = partition(items, left, right, pivot);
sort(items, left, splitIndex - 1);
sort(items, splitIndex, right);

Python

split_index = partition(items, left, right, pivot)
sort(items, left, split_index - 1)
sort(items, split_index, right)

PHP

<?php

$splitIndex = partition($items, $left, $right, $pivot);
sort($items, $left, $splitIndex - 1);
sort($items, $splitIndex, $right);

Java

var splitIndex = partition(items, left, right, pivot);
sort(items, left, splitIndex - 1);
sort(items, splitIndex, right);

Единственный код, который вызывает вопросы — выбор опорного элемента:

const pivot = items[left];

Python

pivot = items[left]

PHP

<?php

$pivot = $items[$left];

Java

var pivot = items[left];

Почему мы всегда выбираем самый левый элемент подмассива?

Средний элемент должен находиться ровно посередине отсортированного массива. В таком случае его называют медианой. Чтобы узнать медиану, нужно иметь отсортированный массив, а чтобы отсортировать массив — знать медиану. Получается замкнутый круг.

На практике необязательно делить массив ровно пополам — достаточно разбить массив на приблизительно равные части — алгоритм все равно будет работать быстро. Если элементы в массиве расположены в случайном порядке, то можно брать любой элемент по счету — в среднем массив будет всегда разбит пополам.

Можно выбрать самый левый элемент в качестве опорного элемента — как видно на примере выше, это работает.

Выше мы написали универсальную функцию, которая может сортировать отдельные подмассивы. Сложность в том, что такой функцией не очень удобно пользоваться — приходится передавать параметры left и right даже тогда, когда надо отсортировать массив целиком.

Чтобы упростить себе жизнь, напишем вспомогательную функцию, которая всегда сортирует массив целиком:

const quicksort = (items) => sort(items, 0, items.length - 1);

const items = [ 57, 10, 52, 43, 55, 93, 34, 24, 99 ];
quicksort(items);
console.log(items); // => [ 10, 24, 34, 43, 52, 55, 57, 93, 99 ]

https://replit.com/@hexlet/js-sorting-qsort#index.js

Python

def quicksort(items):
    sort(items, 0, len(items) - 1)

items = [57, 10, 52, 43, 55, 93, 34, 24, 99]
quicksort(items)
print(items)  # => [10, 24, 34, 43, 52, 55, 57, 93, 99]

https://replit.com/@hexlet/python-sorting-qsort#main.py

PHP

<?php

function quicksort(&$items)
{
    mySort($items, 0, count($items) - 1);
}

$items = [ 57, 10, 52, 43, 55, 93, 34, 24, 99 ];
quicksort($items);
print_r($items); // => [ 10, 24, 34, 43, 52, 55, 57, 93, 99 ]

https://replit.com/@hexlet/php-sorting-qsort#main.php

Java

class App {

    public static void quicksort(int[] items) {
        sort(items, 0, items.length - 1);
    }

    // ...
}

int[] items = { 57, 10, 52, 43, 55, 93, 34, 24, 99 };
App.quicksort(items);
System.out.println(Arrays.toString($items));
// => [ 10, 24, 34, 43, 52, 55, 57, 93, 99 ]

https://replit.com/@hexlet/java-sorting-qsort#src/main/java/Main.java

Быстрая сортировка намного эффективнее сортировки выбором. Причем эта разница особенно видна на больших массивах. Если сортировать миллион элементов, сортировка выбором окажется медленнее в десятки тысяч раз.

Универсальная функция сортировки

Мы реализовали три функции сортировки, каждая из которых упорядочивает в возрастающем порядке элементы простых типов: чисел, дат, строк.

Вспомним пример с интернет-магазином, в котором мы сталкиваемся с более сложной задачей — сортировкой по разным атрибутам. Представим, что нам предстоит сортировать товары по трем атрибутам:

Название — name
Цена — price
Рейтинг — rating

Сам массив выглядит так:

const products = [
  { name: "Телевизор", price: 100000, rating: 9.1 },
  { name: "Холодильник", price: 20000, rating: 8.3 },
  { name: "Пылесос", price: 14000, rating: 7.5 },
  { name: "Стиральная машина", price: 30000, rating: 9.2 },
  { name: "Миелофон", price: 200000, rating: 8.7 },
  { name: "Микроволновка", price: 7000, rating: 8.2 },
  { name: "Проигрыватель", price: 20000, rating: 9.0 },
  { name: "Посудомоечная машина", price: 80000, rating: 7.8 },
  { name: "Мультиварка", price: 5000, rating: 7.1 },
];

Python

products = [
  {"name": "Телевизор", "price": 100000, "rating": 9.1},
  {"name": "Холодильник", "price": 20000, "rating": 8.3},
  {"name": "Пылесос", "price": 14000, "rating": 7.5},
  {"name": "Стиральная машина", "price": 30000, "rating": 9.2},
  {"name": "Миелофон", "price": 200000, "rating": 8.7},
  {"name": "Микроволновка", "price": 7000, "rating": 8.2},
  {"name": "Проигрыватель", "price": 20000, "rating": 9.0},
  {"name": "Посудомоечная машина", "price": 80000, "rating": 7.8},
  {"name": "Мультиварка", "price": 5000, "rating": 7.1},
]

PHP

<?php

$products = [
    ['name' => 'Телевизор', 'price' => 100000, 'rating' => 9.1],
    ['name' => 'Холодильник', 'price' => 20000, 'rating' => 8.3],
    ['name' => 'Пылесос', 'price' => 14000, 'rating' => 7.5],
    ['name' => 'Стиральная машина', 'price' => 30000, 'rating' => 9.2],
    ['name' => 'Миелофон', 'price' => 200000, 'rating' => 8.7],
    ['name' => 'Микроволновка', 'price' => 7000, 'rating' => 8.2],
    ['name' => 'Проигрыватель', 'price' => 20000, 'rating' => 9.0],
    ['name' => 'Посудомоечная машина', 'price' => 80000, 'rating' => 7.8],
    ['name' => 'Мультиварка', 'price' => 5000, 'rating' => 7.1],
];

Java

Map[] products = {
  Map.of ("name", "Телевизор", "price", 100000, "rating", 9.1),
  Map.of ("name", "Холодильник", "price", 20000, "rating", 8.3),
  Map.of ("name", "Пылесос", "price", 14000, "rating", 7.5),
  Map.of ("name", "Стиральная машина", "price", 30000, "rating", 9.2),
  Map.of ("name", "Миелофон", "price", 200000, "rating", 8.7),
  Map.of ("name", "Микроволновка", "price", 7000, "rating", 8.2),
  Map.of ("name", "Проигрыватель", "price", 20000, "rating", 9.0),
  Map.of ("name", "Посудомоечная машина", "price", 80000, "rating", 7.8),
  Map.of ("name", "Мультиварка", "price", 5000, "rating", 7.1)
};

Можно реализовать несколько функций сортировки, но есть и более эффективный способ. Интернет-магазину подойдет универсальная функция сортировки.

Каждую из трех видов сортировок выше можно сделать универсальной — и тогда алгоритм сможет сортировать данные любого типа. Для этого надо добавить еще один параметр — функцию сравнения (компаратор). Универсальная функция сортировки вызывает компаратор каждый раз, когда требуется сравнить два элемента и определить, какой из них больше.

У компаратора два параметра — два элемента массива, которые надо сравнить. Если первый больше второго, компаратор возвращает 1. Если первый меньше второго, компаратор возвращает -1. Если элементы равны, компаратор возвращает 0.

Вот так будет выглядеть компаратор, сравнивающий элементы по цене:

const compareByPrice = (item1, item2) => {
  if (item1.price < item2.price) {
    return -1;
  } else if (item1.price == item2.price) {
    return 0;
  } else {
    return 1;
  }
};

Python

def compare_by_price(item1, item2):
    if item1['price'] < item2['price']:
        return -1
    elif item1['price'] == item2['price']:
        return 0
    else:
        return 1

PHP

<?php

function compareByPrice($item1, $item2)
{
    if ($item1['price'] < $item2['price']) {
        return -1;
    } else if ($item1['price'] == $item2['price']) {
        return 0;
    } else {
        return 1;
    }
}

Java

public static ToIntBiFunction<Map<String, Object>, Map<String, Object>> compareByPrice = (item1, item2) -> {
        var price1 = (int) item1.get("price");
        var price2 = (int) item2.get("price");

        if (price1 < price2) {
            return -1;
        } else if (price1 == price2) {
            return 0;
        } else {
            return 1;
        }
};

А вот так — компаратор, сравнивающий элементы по рейтингу:

const compareByRating = (item1, item2) => {
  if (item1.rating < item2.rating) {
    return -1;
  } else if (item1.rating == item2.rating) {
    return 0;
  } else {
    return 1;
  }
};

Python

def compare_by_rating(item1, item2):
    if item1[rating] < item2[rating]:
        return -1
    elif item1[rating] == item2[rating]:
        return 0
    else:
        return 1

PHP

<?php

function compareByRating($item1, $item2)
{
    if ($item1['rating'] < $item2['rating']) {
        return -1;
    } else if ($item1['rating'] == $item2['rating']) {
        return 0;
    } else {
        return 1;
    }
}

Java

public static ToIntBiFunction<Map<String, Object>, Map<String, Object>> compareByRating = (item1, item2) -> {
        var rating1 = (double) item1.get("rating");
        var rating2 = (double) item2.get("rating");

        if (rating1 < rating2) {
            return -1;
        } else if (rating1 == rating2) {
            return 0;
        } else {
            return 1;
        }
};

Универсальная функция сравнивает два элемента, но не использует операторы «больше» или «меньше». Вместо этого она вызывает компаратор и проверяет результат. Так выглядит универсальная пузырьковая сортировка:

const bubbleSort = (items, comparator) => {
  for (let limit = items.length - 1; limit > 0; limit -= 1) {
    for (let i = 0; i < limit; i += 1) {
      if (comparator(items[i], items[i + 1]) > 0) {
        const temporary = items[i];
        items[i] = items[i + 1];
        items[i + 1] = temporary;
      }
    }
  }
};

https://replit.com/@hexlet/js-sorting-universal#index.js

Python

def bubble_sort(items, comparator):
    for limit in range(len(items) - 1, 0, -1):
        for i in range(limit):
            if comparator(items[i], items[i + 1]) > 0:
                items[i], items[i + 1] = items[i + 1], items[i]

https://replit.com/@hexlet/python-sorting-universal#main.py

PHP

<?php

function bubbleSort(&$items, $comparator)
{
    for ($limit = count($items) - 1; $limit > 0; $limit -= 1) {
        for ($i = 0; $i < $limit; $i += 1) {
            if ($comparator($items[$i], $items[$i + 1]) > 0) {
                $temporary = $items[$i];
                $items[$i] = $items[$i + 1];
                $items[$i + 1] = $temporary;
            }
        }
    }
}

https://replit.com/@hexlet/php-sorting-universal#main.php

Java

class App {
    public static void bubbleSort(Map[] items, ToIntBiFunction comparator) {
        for (var limit = items.length - 1; limit > 0; limit--) {
            for (var i = 0; i < limit; i++) {
                if (comparator.applyAsInt(items[i], items[i + 1]) > 0) {
                    var temporary = items[i];
                    items[i] = items[i + 1];
                    items[i + 1] = temporary;
                }
            }
        }
    }
}

https://replit.com/@hexlet/java-sorting-universal#src/main/java/Main.java

Компаратор также используется, чтобы изменить направление сортировки. Если элементы надо упорядочить по убыванию, новая функция компаратор должна возвращать 1 там, где старая возвращала -1, и наоборот.

Дополнительные материалы

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты

Для полного доступа к курсу нужен базовый план

Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.

Получить доступ

130

курсов

1000

упражнений

2000+

часов теории

3200

тестов