Подсчет по биекции — Комбинаторика

• Теорема Кейли
  • Доказательство с помощью биекции
• Выводы

Самый простой способ посчитать что-либо — это соотнести объекты с чем-то более простым. Например, можно изучить абстрактные операции на бытовых примерах: соотносить числа и множества с книгами и книжными полками.

Это же упрощение работает и в математике: чтобы подсчитать сложные объекты, надо соотносить их с объектами, которые вы уже умеете считать. Для этого используется теорема Кейли. В этом уроке мы рассмотрим эту теорему и докажем ее. Вы узнаете, что такое биекция, а также умная конструкция.

Теорема Кейли

Теорема Кейли применяется, чтобы подсчитать количество меченых прямых деревьев. Другими словами, теорема Кейли помогает ответить на вопрос: «Сколько всего существует деревьев на фиксированном множестве вершин множестве V?».

При этом характер элементов V не важен. Например, мы можем взять такое выражение:

V = [n] В этом случае ответ будет зависеть не от [n], а только от размера V. Обозначим это число через t(n).

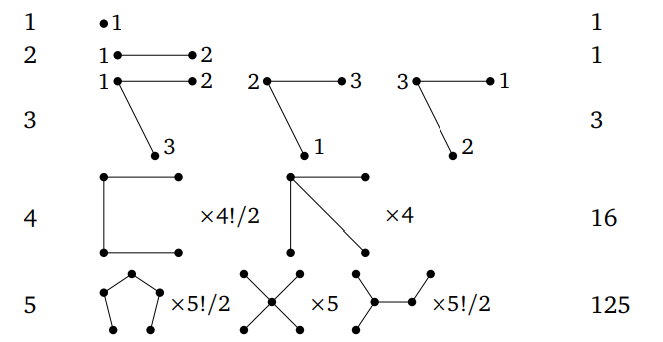
Теперь сгенерируем деревья. Сначала определяем все возможные формы деревьев — то есть немеченые деревья на n вершинах.

Затем найдем все способы присвоить элементам V их метки:

В правой части этой схемы мы видим числа 1, 1, 3, 16 и 125. Они равны n^(n-2).

Таким образом можно сформулировать теорему Кейли:

Для всех n верно, что число прямых деревьев на множестве вершин размера n равно n^(n-2)

Попробуем доказать эту теорему с помощью биекции.

Доказательство с помощью биекции

Код Прюфера – это такой способ кодирования деревьев с n вершинами с помощью последовательности.

Чтобы доказать эту теорему, выполним первый шаг:

Создадим код Прюфера ( y1 , . . . . , yn - 1 ) дерева T на множестве вершин V = [n]

Для этого нам нужно рекурсивно определить три последовательности:

• (x1 , . . . . , xn - 1 )
• ( y1 , . . . . , yn - 1 ) вершин
• (T1 , . . . . , Tn - 1 ) деревьев

Эти последовательности можно определить следующим образом:

• T1 := T
• Для 1 ≤ i ≤ n - 1, пусть xi — вершина степени -1 в Ti с наименьшим индексом
• Для 1 ≤ i ≤ n - 1, пусть yi — сосед xi в Ti
• Для 1 ≤ i ≤ n-2, пусть Ti + 1 := Ti - xi — дерево, которое получили, когда удалили вершины xi и ребра {xi , yi }

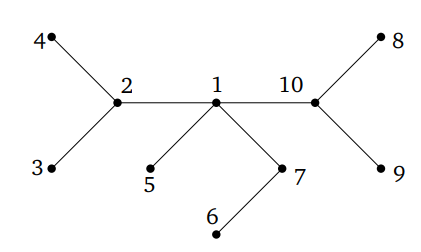
Рассмотрим следующее дерево:

У нас есть две последовательности:

• (x1 , . . . . , x9 ) = (3, 4, 2, 5, 6, 7, 1, 8, 9)
• ( y1 , . . . . , y9 ) = (2, 2, 1, 1, 7, 1, 10, 10, 10)

Рассмотрим код Прюфера ( y1 , . . . . , yn - 1 ).

У каждого дерева есть хотя бы две вершины степени 1, поэтому вершина n никогда не будет удалена. Следовательно, yn - 1 = n.

Выберем k in {1, . . . , n - 2}. Удаляются только вершины степени -1, поэтому степень вершины v в дереве Tk на единицу больше, чем число вхождений v среди ( yk , . . . . , yn-2 ).

Получается, вершины степени 1 в Tk — это те вершины, которые не встречаются в этом выражении:

{x1 , . . . . , xk-1 } cup { yk , . . . . , yn-2 }

Теперь xk — наименьший элемент из [n], который не входит в множество. Такой элемент всегда существует, и у него не более n - 2 членов.

Отсюда следует, что из последовательности ( y1 , . . . . , yn-2 ) можно восстановить:

• (y1 , . . . . , yn - 1 )
• (x1 , . . . . , xn - 1 )

Поэтому мы можем восстановить в таком порядке: Tn - 1 , . . . , T1 = T.

Каждое дерево дает последовательность, с помощью которой можно восстановить уникальное дерево. В этом случае повторное присоединение xk к yk однозначно определено. Поэтому количество последовательностей (y1, . . . ,yn-2) и количество деревьев должны быть равны. Число последовательностей равно n^n-2, так как каждый yi принимает n различных значений.

Биекция — это не единственный способ доказательства теоремы Кейли. Еще есть умная конструкция, которая помогает в подсчетах более сложных структур. Этот прием встречается все чаще, но пока мы не будем останавливаться на нем подробно из-за объемного и трудоемкого доказательства.

Выводы

В этом уроке мы изучили еще один инструмент комбинаторики — теорему Кейли, которая помогает упростить подсчеты и свести их к уже известным объектам.

Чтобы разобраться в этом теореме, мы познакомились с такими фундаментальными понятиями, как биекция и код Прюфера. Эти термины будут полезны далее в курсе по комбинаторике и в других курсах по дискретной математике.