Композиция функций — Функции

• Что такое составные функции
• Свойства составных функций
• Как решать составные функции
• Композиция функции с самой собой
• Выводы

Композиция функций — это процесс объединения двух или более функций в одну функцию. Функция представляет собой некоторое действие. Возьмем приготовление хлеба и переведем этот процесс на язык математики:

• Мука — x
• Приготовление теста из муки с помощью кухонного комбайна — g(x)
• Запекание хлеба в печи — f(x)
• Приготовление хлеба — выход g(x) надо поместить в функцию f(x)
• Готовый хлеб — функция f(g(x)), то есть композиция функций f(x) и g(x)

В этом уроке мы как раз изучим эту тему — посмотрим, что такое композиция функций в математике и как ее вычислить.

Что такое составные функции

В математике составная функция — это операция, при которой две функции порождают новую функцию. В некоторых источниках то же самое явление называется композицией функции.

Возьмем такой простой пример:

• У нас есть две функции — f и g
• Вместе они порождают функцию h
• Составной функцией будет считаться h(x) = g(f(x))

Как видите в примере выше, функция g применяется к функции f. Другими словами, одна функция применяется к результату другой функции.

Давайте посмотрим на математическое определение составной функции:

• Пусть f : A → B и g : B → C — две функции
• Тогда составная функция будет состоять из f и g — это обозначается как g ∘ f
• Составная функция g ∘ f определяется как функция g ∘ f : A → C
• Функция g ∘ f : A → C задается через g ∘ f (x) = g(f (x)), ∀ x ∈ A

На рисунке ниже показано графическое представление составных функций:

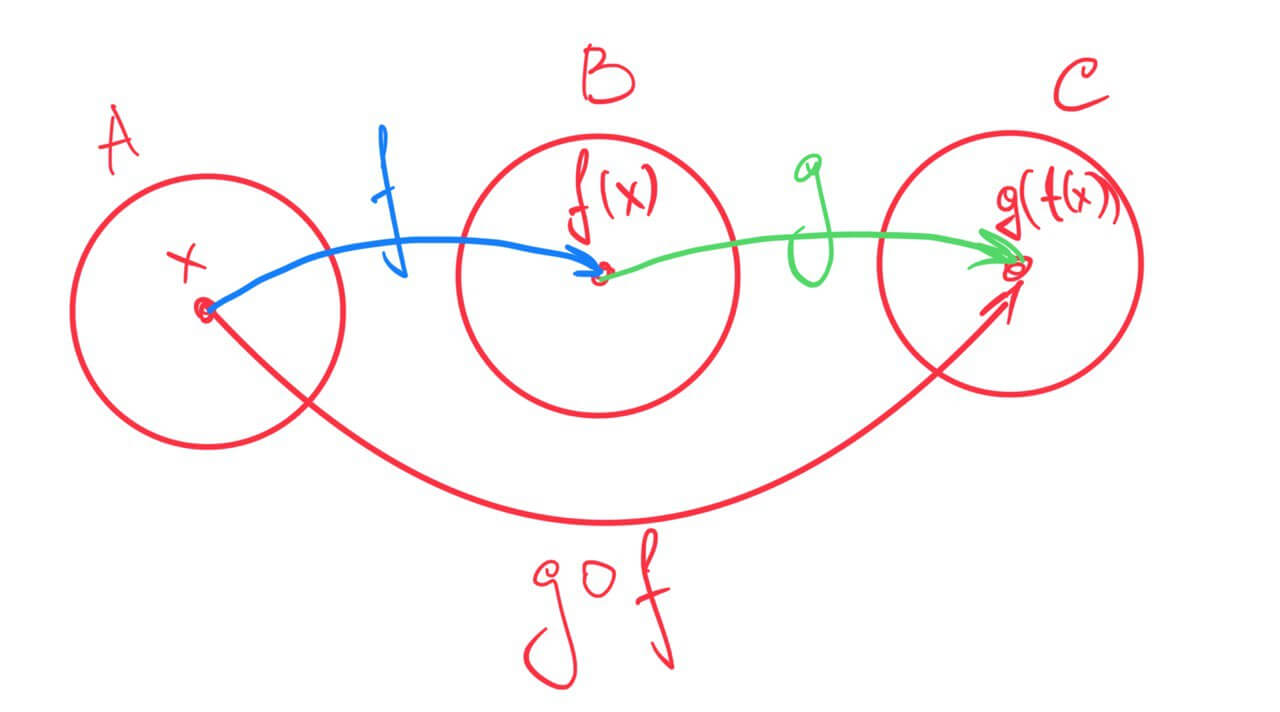
Порядок функции является важным моментом при работе с композицией функций, потому что выражения (f ∘ g) (x) и (g ∘ f) (x) не равны между собой.

Это можно очень хорошо понять на примере. Представим машину, которая сначала запекает торт, а затем украшает его глазурью. Будем рассматривать эти действия как функции:

• Запекание — функция b
• Украшение — функция i

Машина будет производить торт, используя b ∘ i — сначала печь, затем украшать. Но если функции поменять местами (i ∘ f), то машина сначала украсит сырой торт, а сожжет его в печке вместе со всеми украшениями. Такая перестановка действий не сработает, поэтому нам нужны оба домена.

Теперь рассмотрим, как обозначаются составные функции и их области:

• Символ: В обозначении составных функций используется символ, похожий на маленький круг. Так это выглядит на практике — (g∘f)(x)
• Домен: f(g(x)) читается как «f от g от x». В композиции (f ∘ g) (x) домен функции f становится g(x)
• Область: это множество всех значений, которые входят в функцию
• Пример: Если f(x) = 3x+1 и g(x) = x^2, то f от g от x, f(g(x)) = f(x^2) = 3x^2+1

Обратите внимание, что будет, если мы обратим операцию над функцией. Например, если мы возьмем g от f от x, то в итоге получим g(f(x)) = g(3x+1) = (3x+1)^2.

Свойства составных функций

У составных функций есть два основных свойства:

• Ассоциативное
• Коммутативное

Рассмотрим их подробнее.

Ассоциативное свойство:

Если есть три функции f, g и h, то составные функции считаются ассоциативными только тогда и только тогда, когда f ∘ (g ∘ h) = (f ∘ g) ∘ h

Коммутативное свойство:

Две функции f и g коммутативны друг с другом тогда и только тогда, когда g ∘ f = f ∘ g

Есть еще несколько свойств составных функций:

• Композиция функций один-к-одному всегда один к одному
• Композиция двух онто-функций всегда онто
• Обратная композиция двух функций f и g равна композиции обратных обеих функций, например, (f ∘ g)^-1 = (g^-1 ∘ f^-1)

Как решать составные функции

В математике решение составной функции — это получение композиции двух функций. Выполним следующие шаги, чтобы понять, как это выглядит на практике.

Шаг 1: Возьмем две функции:

f(x) = x^2 g(x) = 3x

Запишем их в виде составной функции:

(f ∘ g) (x)

Также ее можно записать как f[g(x)].

Шаг 2: Возьмем переменную x, которая есть во внешней функции. Заменим ее внутренней функцией, взяв за основу отдельные функции:

Поскольку g(x) = 3x, результат на этом шаге будет выглядеть так:

(f ∘ g)(x) = f(3x)

Шаг 3: Далее мы можем упростить функцию.

Поскольку f(x) = x^2, результат на этом шаге будет выглядеть так:

(f ∘ g)(x) = f(3x) = (3x)^2=9x^2

Таким образом, мы за три шага решили составную функцию.

Композиция функции с самой собой

Также существуют составные функции, которые содержат композицию функции с самой собой.

Предположим, что f — это функция. Тогда композиция функции f с самой собой будет выглядеть так:

(f∘f)(x) = f(f(x))

Давайте разберемся в этом на практике. Возьмем такой пример:

Условие: f(x) = 3x^2

Исходя из этого условия, попробуем найти (f∘f)(x).

Решение будет выглядеть так:

Дано: f(x) = 3x^2

(f∘f)(x) = f(f(x))

=f(3x^2)

=3(3x^2)^2

=3*9x^4

=27x^4

Выводы

В этом уроке мы рассмотрели композицию функций — это действие, при котором функции a и b объединяются для получения новой функции. Эта новая функция c формулируется как c(x) = b(a(x)).

Это означает, что функция b применяется к функции x. Другими словами, когда функция применяется к выходу другой функции, она называется составной функцией.

Самостоятельная работа

Задача 1

По условию нам дано:

• f(x) = 2x
• g(x) = x+1

Найдите (f∘g)(x), если x = 1.

Сначала обращаемся к условию:

• f (x) = 2x
• g(x) = x+ 1

Вычисляем композицию f из g:

(f∘g)(x) = f(g(x)) = f(x+1) = 2(x+1)

Теперь положим значение x = 1:

f(g(1)) = 2(1+1) = 2 (2) = 4

Ответ: 4

Задача 2

По условию нам дано:

• f(x) = 2x +1
• g(x) = -x^2

Найдите (g∘f)(x) для x = 2.

Подставим значения из условия в выражение g(f(x)):

g(f(x)) = g(2x+1) = -(2x+1)^2

Теперь положим x =2:

g(f(2)) = -(2,2+1)^2 = -(4+1)^2 =-(5)^2 =-25

Ответ: -25

Задача 3

По условию у нас есть три функции:

• f(x) = x
• g(x) = 2x
• h(x) = 3x

Найдите композицию этих функций [f ∘ (g ∘ h)] (x) для x = -1.

Подставим функции из условия в выражение [f ∘ (g ∘ h)] (x):

[f ∘ (g ∘ h)] (x) = f ∘ (g(h(x))) = f ∘ g(3x) =f(2(3x)) =f(6x) =6x

Возьмем x = -1:

[f ∘ (g ∘ h)

(-1) = 6(-1) = -6]

Ответ: -6

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты