Равенство — Функции

• Что такое равные функции
• Как определяется равенство функций
  • Обычный способ определения равенства функции
  • Категориальный способ определения равенства функции
• Ограничения функций
• Булевы функции и комбинаторные сети
• Выводы

Два числа равны, если они представляют собой одно и то же число. Две переменные равны, если они представляют собой одно и то же число. Следуя этим очевидным понятиям, мы можем сказать, что две функции равны, если они представляют собой одну и ту же функцию.

Но все не так очевидно: само понятие «равные функции» указывает на то, что существует более одного способа представления функции. Другими словами, вопрос о равенстве двух функций возникает, когда две формы функции дают одинаковые значения. Это происходит, потому что есть альтернативные способы представления одной и той же математической сущности.

В математике такие случаи иногда встречаются. В этом уроке мы рассмотрим их подробнее и выясним, что такое равные функции и как использовать их.

Что такое равные функции

Для начала рассмотрим функцию модуля. Возьмем два эквивалентных выражения:

• f(x)=|x|
• g(x)=√{x^2}

Эти две формы функции дают одинаковые значения для всех действительных значений x. Таким образом, эти две функции f(x) и g(x) являются равными функциями.

С другой стороны, существуют эквивалентные формы — они представляют одинаковые значения, но не для всех значений x в областях двух определений. Рассмотрим такой пример:

(x)=2log(e)x g(x)=log(e)x^2

Логарифмическая функция f(x) определена для x>0. Это означает, что ее область — это (0, ∞). При этом для логарифмической функции g(x) областью будет => x^2 > 0.

Это неравенство справедливо для всех значений x, кроме x=0. Значит, область g(x) - R-{0}.

Очевидно, что домены двух функций не равны: для значения x = -1 функция g(x) дает значение, при этом функция f(x) не определена для этого значения x.

Таким образом, два уравнения не равны. Однако две функции равны, если мы ограничим рассмотрение домена пересечением двух доменов. Следовательно:

f(x)=g(x); x ∈ (0,∞)

Существует еще одна возможность. Две эквивалентные формы имеют одинаковые домены, но дают разный набор значений. В этом случае две функции также не равны.

Как определяется равенство функций

Чтобы вычислить равенство функции, используют два способа:

• Обычный
• Категориальный

Разберем каждый способ подробнее.

Обычный способ определения равенства функции

Информация в функции состоит из:

• Входов, которые мы можем ей предоставить
• Выходов, которые эти входы производят

Математики определяют функцию как набор пар элементов (x,y), где появляющиеся x — возможные входы, а пара (x,y) находится в наборе, если y является выходом для входа x.

Есть разница между функцией и просто отношением. В случае с функцией для данного x, который является возможным входом, существует только одна пара (x,y). То есть у каждого входа есть уникальный выход.

Множество x, которые появляются, называется областью функции, а множество y — диапазоном функции. В итоге равенство функций сводится к понятию равенства множеств: две функции или два набора пар равны, если они равны как множества — содержат одинаковые пары.

У равных функций обязательно есть равные области и диапазоны. Обычно начинают с множества X и множества Y и определяют функцию от X к Y как подмножество S декартово произведения X * Y, такое, что множество x, которые появляются в паре (x,y) в S, состоит из всего X, и для каждого x в X существует ровно один y в Y, такой, что (x,y) находится в S.

Категориальный способ определения равенства функции

Этот способ мышления наиболее заметен, когда человек рассматривает вещи с точки зрения теории категорий, а не просто теории множеств. Рассмотрим функцию от множества действительных чисел к самой себе. Она задана формулой f(x) = x^2. Область действия этой функции — множество действительных чисел ≥ 0 — неотрицательных действительных чисел.

Теперь рассмотрим функцию от множества действительных чисел к множеству неотрицательных действительных чисел. Она задана формулой g(x) = x^2. Равна ли функция f формуле g? Как множества — они одинаковы, поэтому по общему определению, приведенному выше, они равны. Но есть ситуации, когда необходимо провести различие между этими двумя понятиями.

Если начать с множества X и множества Y и говорить, что f — это функция от X к Y, то X называется доменом, а Y — кодоменом f.

В категориальном мышлении функция — это не просто набор пар. Это набор пар вместе с информацией о его кодомене. Две функции считаются равными, если они равны как множества, и их кодомены равны. Получается, что функции f и g не считаются равными. Это называется категориальным способом мышления, потому что в теории категорий примитивными вещами являются не множества, а так называемые объекты. Функция между этими объектами называется морфизмом. Она тоже считается примитивным объектом.

Обычно об объектах думают как об абстрактных вещах, а о морфизмах — как о стрелках между этими вещами. В некоторых контекстах объекты являются реальными множествами, а морфизмы — реальными функциями между этими множествами. Но в других случаях объекты не будут множествами, как и функции.

Поскольку функции определяются как подмножества произведения двух множеств — как множества упорядоченных пар — две функции равны, когда они равны как множества. Рассмотрим такое определение:

Пусть F, G : X -> Y — две функции. Функции F и G равны тогда и только тогда, когда они содержат одинаковые упорядоченные пары

Существует теорема, которая выводит ряд правил для эквивалентных функций. Приведем ее вывод:

Пусть F и G — функции, такие, что F = G. Тогда:

• Домен (F) = домен (G)
• Диапазон (F) = диапазон (G)
• Для каждого x ∈ (F), F(x) = G(x)

Ограничения функций

Рассмотрим такой пример — нужно написать алгоритм для вычисления sqrt(R(x)) = x^2 для x ∈ R.

Введем такое ограничение — в качестве входных данных должны использоваться только натуральные числа. Уже этим утверждением можно заставить тот же алгоритм определить sqrtN, функцию от N до N.

Это пример ограничения функции на меньшую область. Посмотрим, как эта же мысль выражается в формальном определении:

Пусть:

• A, B и C — это множества, такие, что B C A
• F : A → C — функция

В таком случае ограничение F на B будет обозначаться как F|_B.

Обозначим функцию из B в C, определенную как множество:

F|_B = {(x, y) ∈ F :x B}

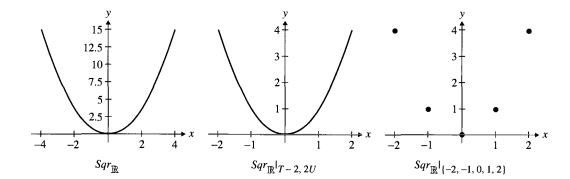
Ниже показаны два примера ограничений функции sqrtR:

Булевы функции и комбинаторные сети

В булевой алгебре используются двоичные переменные и логические операции. Алгебраическое выражение известно как булево выражение, оно используется для описания булевой функции. Булево выражение состоит из постоянного значения 1 и 0, символов логических операций и двоичных переменных.

Эквивалентность для булевых функций определяется так:

Булева функция от n булевых переменных — это функция вида: B :{0, 1} x {0, 1} x ... x {0, 1} --> {0, 1}

Область B содержит 2^n элементов. Каждому элементу 2^n упорядоченных n-кортежей присваивается значение 0 или 1. Пример булевой функции на трех булевых переменных приведен в таблице:

Булевы функции могут представлять собой набор переключателей, которые реагируют соответствующим образом. Также это может быть набор условий, которые нужно выполнить для определенных действий.

Иногда удобно представлять функции в виде таблицы. Но проблема часто заключается в том, чтобы встроить эту функцию в комбинаторную сеть.

Посмотрим, как представить функцию в терминах одной из этих нормальных форм.

Для функции из таблицы дизъюнктивная нормальная форма имеет вид:

F(p, q, r) = (p A q A r) V (p A -q A r) V (p A -q A -r) V (-p A q A r) V (-p A q A -'r) V (-p A -q A -'r)

Комбинаторная схема — это схема, показанная на рисунке:

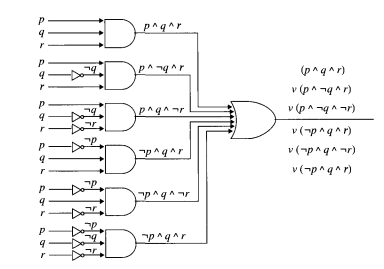
Обратите внимание, что у ворот есть несколько входов. Это сделано для удобства или по другим причинам. Мы также можем записать ворота с тремя входами как набор ворот с двумя входами каждый, как показано на рисунке ниже:

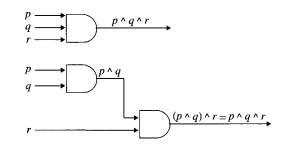
Выводы

В этом уроке мы рассмотрели решения эквивалентных уравнений на заданном интервале. Повторим главную мысль урока — две функции можно считать равными, если они имеют эквивалентные домен и кодомен. Их значения также должны быть одинаковыми для всех элементов области.

Самостоятельная работа

Задача №1

Определите, являются ли f(x) и g(x) тождественными функциями:

• f(x)=x/x^2
• g(x)=1/x

Задача №2

Определите, являются ли f(x) и g(x) тождественными функциями:

• f(x)=log_e(x)-log_e(x^2+1)
• g(x)=log_e(x/(1+x^2))

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты