- Возрастающие и убывающие функции
- Правила проверки функций
- Возрастание и убывание на графике
- Свойства возрастающих и убывающих функций
- Выводы
Ранее в курсе мы уже рассматривали разные свойства функций. Сегодня мы разберем еще одно свойство — возрастание и убывание.
В этом уроке мы рассмотрим понятие возрастающей и убывающей функций, их свойства, графическое представление, теоремы для проверки возрастающих и убывающих функций, а также примеры для лучшего понимания.
Возрастающие и убывающие функции
Возрастающие и убывающие функции — это функции, для которых значение производной увеличивается и уменьшается соответственно с изменением значения x.
Рассмотрим подробнее, что значит это определение. Для проверки поведения возрастающих и убывающих функций используется производная функции . Считается, что:
-
Функция возрастает, если значение увеличивается с ростом значения
-
Функция убывает, если значение уменьшается с ростом значения x
Давайте рассмотрим формальные определения возрастающей и убывающей функции, чтобы понять их смысл.
Во всех определениях выше соблюдаются общие условия. Возрастание и убывание функции рассматривается:
-
На интервале
-
Для любых двух значений и в
-
Если значение
А теперь рассмотрим сами определения:
-
Возрастающая функция — функция возрастает, если
-
Убывающая функция — функция убывает, если
-
Строго возрастающая функция — функция строго возрастает, если
-
Строго убывающая функция — функция строго убывает, если
Правила проверки функций
Чтобы проверить возрастание и убывание, можно использовать производную функции. Посмотрим, как это работает на практике.
Предположим, что функция дифференцируема на открытом интервале , тогда она определяется так:
-
Если на , то функция является возрастающей на
-
Если на , то функция является убывающей функцией на
Чтобы разобраться подробнее, возьмем такой пример:
-
Рассмотрим , определенную для всех действительных чисел
-
Производная от имеет вид
-
Мы знаем, что квадрат числа всегда больше или равен , поэтому для всех
-
Следовательно, — возрастающая функция
Возрастание и убывание на графике
Теперь мы знаем значение и определение возрастающих и убывающих функций. Дальше давайте посмотрим на графическое представление возрастающих и убывающих функций, которое поможет нам понять поведение функций.
Кроме производной, есть еще один способ определить возрастание и убывание функции. Можно взглянуть на ее график:
-
Функция возрастает, если график идет вверх по мере продвижения к правой стороне оси
-
Функция убывает, график идет вниз по мере продвижения к правой стороне оси
Посмотрите на этот пример:
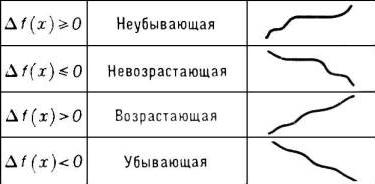
На приведенных выше графиках показано графически представлены все четыре типа функций:
-
Строго возрастающая
-
Строго убывающая
-
Возрастающая
-
Убывающая
Как видно из графиков, возрастающая функция ведет себя по-разному:
-
В одних частях графика есть строго возрастающие интервалы
-
В других частях графика есть интервалы, где функция постоянна
Аналогично, убывающая функция состоит из интервалов, где функция строго убывает и где функция постоянна.
Свойства возрастающих и убывающих функций
Выше вы научились проверять, является ли функция возрастающей или убывающей.
Теперь давайте рассмотрим алгебраические свойства возрастающих и убывающих функций. Они помогут вам проводить операции с функциями.
Есть два свойства, связанные с суммами:
-
Если функции и являются возрастающими на открытом интервале , то сумма функций также возрастает на этом интервале
-
Если функции и — убывающие функции на открытом интервале , то сумма функций также убывает на этом интервале
Еще два свойства связаны с произведениями:
-
Если функции и — возрастающие функции на открытом интервале и , на , то произведение функций также возрастает на этом интервале
-
Если функции и — убывающие функции на открытом интервале и на , то произведение функций также убывает на этом интервале
Еще несколько свойств связаны с обратными функциями:
-
Если функция — возрастающая функция на открытом интервале , то обратная функция убывает на этом интервале
-
Если функция — убывающая функция на открытом интервале , то противоположная функция — возрастающая на этом интервале
-
Если функция — возрастающая функция на открытом интервале , то обратная функция убывает на этом интервале
-
Если функция — убывающая функция на открытом интервале , то обратная функция возрастает на этом интервале
Выводы
В этом уроке мы узнали, как работают возрастающие и убывающие функции. Теперь мы умеет определять это свойство двумя способами — через производную и по графику. Также мы познакомились со свойствами возрастающих и убывающих функций — они помогут вам проводить операции с функциями.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
