Частичные функции — Функции

• Зачем нужны частичные функции
• Как обозначаются частичные функции
• Формальное определение частичной функции
• Примеры частичных функций
  • Пример 1
  • Пример 2
  • Пример 3
• Выводы

В этом курсе мы уже обсуждали, что компьютерные программы связаны с математическими функциями. У программ есть:

• Вход — любая строка символов, которую ввели в программу
• Выход — любая строка символов, которую вывела программа после выполнения
• Функция — операция, которая превращает строку со входа в строку на выходе

При определенных условиях программы попадают в бесконечные циклы. Из-за этого они не дают никакого результата. Программа не может вычислить функцию от входных данных, потому что на каждый входной сигнал ей нужен ровно один выходной сигнал.

В таких случаях вычисляется частичная функция, которую мы и рассмотрим в этом уроке.

Зачем нужны частичные функции

Для начала вспомним, что числа бывают разных видов, в том числе:

• Вещественные — это любые числа, включая десятичные и дробные (например, 1, 1.1 и 1.2)
• Натуральные — это только целые числа (например, 1, 2 и 3)

А теперь возьмем функцию f(x) = x/3 и определим ее для разных видов чисел.

В первом случае все сработает хорошо:

• Мы заранее ограничим область функции вещественными числами
• Потом возьмем на вход вещественные числа
• Применим функцию f(x) = x/3

На выходе получим тоже вещественные числа:

• Если x=1, то f(x) = 1/3 = 0.33
• Если x=1.1, то f(x) = 1.1/3 = 0.36
• Если x=1.2, то f(x) = 1.2/3 = 0.4

Здесь функция сработает во всех случаях, так что ее можно считать полностью определенной функцией.

Во втором случае все сработает не так гладко:

• Мы заранее ограничим область функции натуральными числами
• Потом возьмем на вход натуральные числа
• Применим функцию f(x) = x/3

На выходе мы получим такой результат:

• Если x=1, то f(x) = 1/3=0.33
• Если x=2, то f(x) = 2/3 =0.66
• Если x=3, то f(x) = 3/3=1

Сложность в том, что для x=1 и x=2 выходом функции будет дробное число, а не натуральное. Изначально мы ограничили функцию только натуральными числами, но на выходе получили дробные.

Значит, функция сработает не во всех случаях, поэтому ее называют частично определенной функцией.

Другими словами, это частичная функция — то есть функция, которая работает только частично. Она обозначается так:

f:A → B

Такие сложности с входными данными могут встретиться в программировании. Если в этом случае опираться только на полностью определенные функции, то программа может работать со сбоями и уходить в бесконечные циклы.

Как обозначаются частичные функции

Теперь разберем другой пример частичной функции.

Предположим, что мы изучаем таблицу с почтовыми расходами. В ней обозначено, сколько стоит пересылка посылок разного веса:

В этой таблице обозначены диапазоны. Например, за три доллара можно отправить груз, который весит более 1 кг, но меньше или равно 5 кг.

Обратите внимание, что в таблице не указана стоимость пересылки грузов более 15 кг. Если бы мы использовали функцию, она была бы частичной, потому что в таблице дана не вся информация.

Можно дополнить таблицу и расширить правило — например, указать, что посылки весом более 15 кг стоят $9. Тогда функция будет полной.

Такие примеры помогают понять, как частичные функции применяются на практике. Они помогают изучать вычислимость — выяснять, какие функции можно вычислить с помощью программ.

Формальное определение частичной функции

Теперь посмотрим на частичные функции с точки зрения математики. Ее формальное определение можно сформулировать так:

Частичная функция F с областью определения X и кодоменом Y — это подмножество X * Y. При этом для каждого x ∈ X существует одно самое большое y с (x, y) ∈ F.

Такая функция называется «частичной функцией F из X в Y» и обозначается так:

F : X → Y

Областью частичной функции F : X → Y является множество:

{x ∈ X: для некоторого y ∈ Y, (x, y) ∈ F}

Когда F называют частичной функцией, подразумевается, что в ее области определения существует какой-либо x, при котором F(x) не определена. При этом он не обязательно существует.

Примеры частичных функций

Чтобы закрепить знания о частичных функциях, разберем несколько примеров.

Пример 1

Вычитание на N — это частичная функция:

• Ее область определения — N 2
• Ее кодомен — N

Для i > j, i - j не определено на N, поэтому область вычитания можно обозначить так:

{(i, j) ∈ N^2 : i > j}

Диапазон (-) равен N. Чтобы показать, что произвольное n ∈ N находится в диапазоне (-), заметим, что n = n -0.

Пример 2

Деление на R — это частичная функция. Ее область определения — R^2, ее кодомен — R, но ее область — это:

{(x, y) ∈ R^2 : y A 0}

Ее диапазон — R.

Пример 3

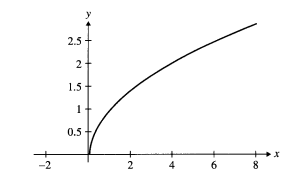
Для x ∈ R пусть sqrt(x) — неотрицательный квадратный корень из x. Тогда это частичная функция, так как sqrt(x) не определена для x > 0. Область определения — R, а ее кодомен — R. Диапазон — [0, oo].

Пусть G — подмножество R. G — это график частичной функции, если каждый раз при x0 ∈ X вертикальная прямая x = xo пересекает G не более чем в одной точке. Это называется тестом на вертикальную линию для частичной функции.

На рисунке показано подмножество R x R, которое не является функцией, так как вертикальная линия x = -1 не пересекает график. Это частичная функцией, так как ни одна вертикальная линия, которая определяется элементом ее области, не пересекает график более одного раза:

Выводы

В этом уроке мы изучили частичные функции — это такие функции, которые срабатывают только частично. Также их называют частично определенными функциями, потому что не все выходные значения будут попадать в заранее определенную область функции.

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты