Понятие функции как правила важно для всех, кто начинает заниматься программированием. В этом уроке мы разберем эту тему на примерах.
Что такое функция как правило
Функция — это уравнение, которое показывает связь между входом и выходом , причем для каждого входа существует ровно один выход.
Представим покупателя, который хочет купить товар на развес — например, яблоки. Он решает купить килограммов, продавец умножает это число на цену, и мы получаем — сумму покупки.
В этой задаче есть две переменные:
-
Независимая переменная — это вес товара , так так эту переменную покупатель меняет сам
-
Зависимая переменная — это сумма покупки , ведь она зависит от веса товара
Для обозначений можно использовать такие термины:
-
Вес товара = Входная переменная = Независимая переменная = Домен
-
Сумма покупки = Выходная переменная = Зависимая переменная = Диапазон
Функции обычно представлены правилом — то есть свойством, в котором зависимая переменная выражается в терминах независимой переменной , например:
Еще можно представить функцию в виде графика. Самый простой способ построить график — сначала составить таблицу с входами и соответствующими выходами. Снова используем пример с яблоками:
Вход, килограмм |
Выход, рублей |
|
|
|
|
|
|
|
|
Пара входного значения и соответствующего выходного значения называется упорядоченной парой. Обычно пару записывают так:
На графике упорядоченные пары обозначаются так:
-
Входное значение соответствует горизонтальной оси
-
Выходное значение соответствует вертикальной оси
Таким образом, мы можем записать наши значения в виде упорядоченных пар:
-
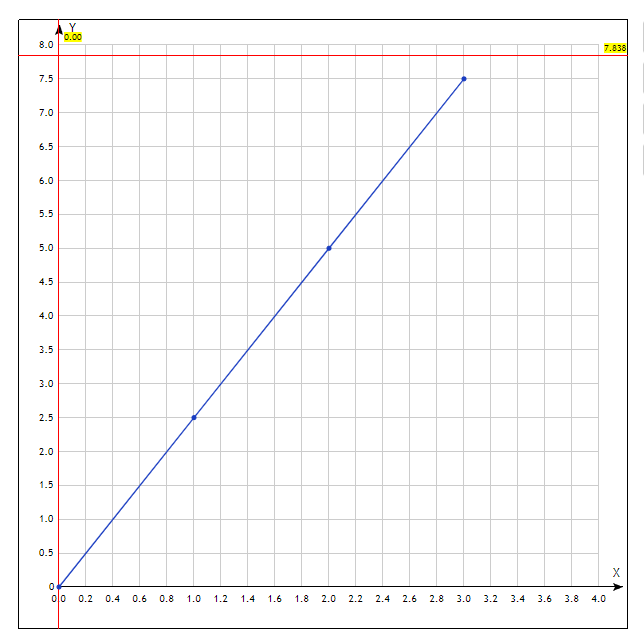
— эта упорядоченная пара также называется началом координат
-
-
-
Эти упорядоченные пары можно построить в виде графика:
Сопоставление набора входов с соответствующими выходами называется отношением. Каждая функция является отношением, но не все отношения являются функциями. В примере выше мы уже увидели, что каждый вход (вес яблок) дает ровно один выход (сумму покупки) — так работают все функции.
Если вы не уверены, является ли отношение функцией или нет, можно провести вертикальную линию прямо через график. Если зависимость не является функцией, то график будет содержать по крайней мере две точки с одинаковой координатой , но с разными координатами .
Как эти правила работают на практике
Чтобы подробнее разобраться в этой теме, изучим различные функции как правила на примерах определения функции.
Функция с несколькими характеристиками
Перейдем к первому примеру. Функцию могут определять следующие правила:
-
Пусть — функция с доменом и кодоменом, равными
-
Эта функция выдает для четных входов и для нечетных
-
Для из попробуем вычислить . Это можно сделать, например, так:
input N
Fact = 1
while N > 0
Fact = Fact. N
N=N-l
print FactСам код не является функцией:
-
Код — это один из способов реализации правила, который определяет функцию
-
Функция — это связь между входом и выходом
Следовательно, множество различных правил могут привести к одной и той же функции.
Идентичные функции
Используя правила, мы можем добавлять функции дополнительные характеристики или ограничения.
Например, следующие два алгоритма вычисляют одну и ту же функцию:
-
Для любого из можно вывести
-
Для любого из можно вывести
С помощью этих правил мы можем показать идентичность функций.
Решение от обратного
Зная правило, мы можем вывести функцию. Посмотрим, как это работает на примере:
Пусть — правило с доменом и кодоменом, равными . Это правило выводит на каждый вход
Представьте, что мы хотим показать, что это правило не определяет функцию. Решение выглядит так:
не определена, так как не входит в кодомен. Поэтому — это не функция
Выводы
В этом уроке мы узнали, как ведет себя функция, если мы воспринимаем ее как функцию. В этом случае функция — это уравнение, которое показывает связь между входом и выходом , причем для каждого входа существует ровно один выход.
Эти знания помогут вам в программировании, ведь умение работать с функциями необходимо в работе с большинством современных языков программирования.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
