Подграфы — Теория графов

• Что такое подграфы
• Индуцированные подграфы
• Подграфы и клики
• Независимое множество
• Выводы

В этом уроке мы разберем, что такое подграфы, какие они бывают и как выглядят. Эти инструменты упростят работу со сложными графами

Что такое подграфы

Подграф — это часть графа, в которой мы берем некоторые его вершины и ребра. Другими словами, граф H является подграфом графа G, если вершины и ребра H являются подмножеством вершин и ребер G.

Ниже слева показан граф. Части исходного графа, которые не являются частью подграфа, показаны серым цветом и пунктирными линиями, хотя обычно их просто опускают:

Обратите внимание, что если ребро входит в подграф, то обе его конечные точки должны входить в него. Не имеет смысла иметь ребро без конечной точки.

Существует несколько видов подграфов, которые мы и разберем далее в уроке.

Индуцированные подграфы

Чтобы лучше понять этот вид подграфов, обратимся к еще одному понятию — инцидентным вершинам. Так называют вершины, если у них есть общее ребро. Например, если между вершинами A и B есть ребро, значит A и B считаются инцидентными.

Индуцированными называют подграфы, в которых все вершины включает в себя все ребра исходного графа, инцидентные этой вершине.

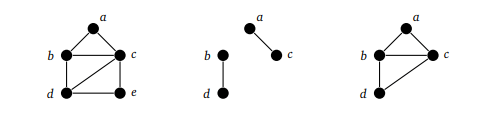
Для наглядности посмотрим на графы ниже:

Здесь изображено три графа:

• Исходный граф, из которого следуют следующие два подграфа
• Неиндуцированный подграф. Он включает вершины a, b, c и d, но не повторяет все ребра с этими вершинами. На исходном графе показаны пять ребер с этими вершинами AB, AC, BC, BD, CD. На подграфе всего два ребра — не хватает BC, AB и CD
• Индуцированный подграф. Он включает вершины a, b, c и d и повторяет все ребра с этими вершинами — AB, AC, BC, BD, CD

Когда нам нужно удалить вершины из графа, мы также должны удалить все ребра, инцидентные этим вершинам. Посмотрим на таком примере:

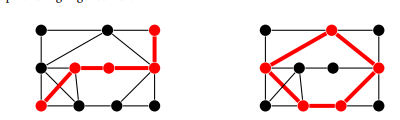
Ниже показан граф и два подграфа после удаления вершин:

• Исходный граф
• Подграф с удаленной вершиной a — значит, мы должны удалить четыре ее ребра
• Подграф с удаленными вершинами b и c — значит, мы должны удалить ребра с этими вершинами и в итоге разбить граф на две части

Если G — граф, а S — подмножество его вершин, то мы удалить вершины и обозначить новый граф через G - S. Если S состоит только из одной вершины v, то вместо этого мы будем писать G - v. Если удаляем только одно ребро e, обозначим это G - e.

Подграфы и клики

В работе с подграфами часто употребляется термин «клика» — это подмножество вершин графа, любые две из которых соединены ребром. Другими словами, это объединение смежных вершин.

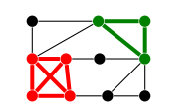
Посмотрим на примере:

На этом графе у нас есть две клики:

• Из четырех вершин в левом нижнем углу (обозначена красным)
• Из трех вершин в правом верхнем углу (обозначена зеленым)

Чтобы точнее понять, что такое клика, представьте социальную сеть. По сути — это граф. Люди — это вершины, а ребра — это отношения людей между собой. Кликой в этом графе можно назвать группу друзей, коллег или любых других знакомых людей.

Особенно часто клики упоминают в работе с циклами и путями в графах. Примеры пути и цикла в графе:

Когда мы говорим, что граф содержит путь или цикл, значит, в нем есть подграф с кликой в несколько вершин, который является путем или циклом.

Независимое множество

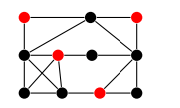
Существует и противоположность клики — независимое множество. Это набор вершин в графе, в котором ни одна вершина не является смежной с другой.

Снова представим граф — социальную сеть. Независимое множество в нем — это набор людей, которые все незнакомы друг с другом.

Так независимое множество выглядит в графе:

Выводы

В этом уроке вы узнали больше о подграфах, кликах и независимых множествах. Теперь вы сможете эффективнее работать с сложными графами и большим количеством вершин, ведь вы сможете разделить запутанный граф на несколько подграфов и изучить отдельные клики.

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты