Двудольные графы — Теория графов

• Что такое двудольный граф
• Как определить, что граф двудольный
• Как доказать теорему о двудольных графах
• Что такое полный двудольный граф

В этом уроке мы разберем еще один тип графа — двудольный. Узнаем, что это за граф, и как его определить.

Что такое двудольный граф

Двудольный граф — это граф, вершины которого можно разбить на две части. При этом ребра будут проходить только между частями, но никогда внутри одной из них.

Так выглядят двудольные графы:

Вершины графа разбиты на две части — верхнюю и нижнюю. Пересечения возможны только между двумя частями, но не внутри них. При этом верхняя и нижняя части — независимые множества.

Обычно двудольные графы рисуют так, чтобы множество X располагалось сверху, а множество Y — снизу. Несмотря на это, не все двудольные графы рисуются именно так. Например, ниже показаны двудольные сетки:

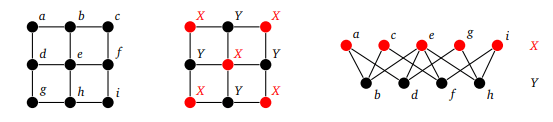
Как определить, что граф двудольный

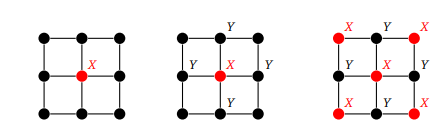
Чтобы определить двудольный граф, начните с любой вершины и пометьте ее буквой X. Каждую из ее соседей пометьте буквой Y, а далее снова пометьте каждую из соседей Y буквой X. Продолжайте помечать вершины и их соседей противоположными метками.

Если получится, что у двух соседних вершин одинаковые метки или какая-то вершина окажется помеченной и X, и Y, значит, граф — не двудольный. Если это не произошло, граф — двудольный. Пример показан ниже:

Предположим, мы попробуем алгоритм на треугольнике K3. Начнем с того, что обозначим вершину X. Затем две соседние вершины обозначим Y. Далее появляется проблема, так как эти вершины — смежные. Аналогичная проблема возникает и C5:

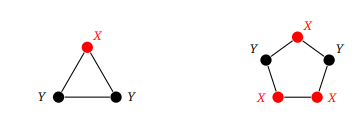
Такое происходит только с нечетными циклами, поэтому у двудольных графов их не бывает. Нечетные циклы — это единственное, чего не может быть у двудольных графов. Докажем это.

Как доказать теорему о двудольных графах

Если граф двудольный, то у любого цикла должна быть четная длина. Чтобы убедиться в этом, начнем с предположения, что два двусоставных множества называются X и Y. Выберем любой цикл в графе и пометим вершины X и Y.

Предположим, мы начинаем трассировку с вершины X. Тогда вторая, четвертая, шестая и следующие четные вершины находятся в X, а остальные — в Y. Когда мы вернемся в начальную вершину, пройдем четное количество шагов. Это значит, что у цикла четная длина:

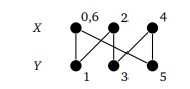
Предположим, что у нас есть граф, в котором нет нечетных циклов. Выберем любую компоненту графа и любую вершину в ней. Пусть X — все вершины компоненты на четном расстоянии от a, а Y — все вершины компоненты на нечетном расстоянии от a.

Мы утверждаем, что это образует двудольное разбиение компоненты. Для этого покажем, что нет ребер ни внутри X, ни внутри Y.

Предположим, что существует такое ребро между вершинами u и v, которые находятся в X или в Y. Значит, u и v находятся либо на четном расстоянии от a, либо на нечетном.

Напомним, что расстояние между вершинами — это длина кратчайшего пути между ними. Рассмотрим кратчайшие пути из a → u и из a → v. Пусть b — последняя общая вершина этих путей. Путь b → u, за которым следует ребро uv, а затем путь v → b образует цикл.

Его длина — это сумма слагаемых:

• 1
• Расстояние от b до u
• Расстояние от b до v

При этом сумма этих слагаемых будет четной. Внутри X и внутри Y не может быть ни одного ребра. Таким образом, X и Y образуют двудольное разбиение компонента. Мы можем проделать тот же процесс для каждой компоненты, чтобы получить двудольное разбиение всего графа.

Пример нечетного цикла, который создали во второй части доказательства:

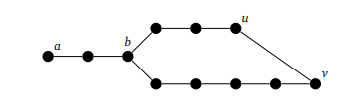
Теперь нужно выбрать вершину и разбить граф на две группы:

• Вершины, которые находятся на четном расстоянии от выбранной вершины
• Вершины, которые находятся на нечетном расстоянии от выбранной вершины

Это основная идея доказательства. Во многих теоремах в теории графов есть одна большая идея, вокруг которой вращается доказательство.

Что такое полный двудольный граф

У двудольных графов есть еще один класс — полные двудольные графы. У них есть возможные ребра между двумя частями. Km, n обозначает полный двудольный граф, одна часть которого состоит из m вершин, а другая — n вершин. Например:

Мы разобрали, что такое двудольные графы и как они выглядят. Теперь вы знаете, как провести доказательство того, что граф двудольный и какие его свойства указывают на это.

Самостоятельная работа

Задача №1

Является ли следующий граф двудольным?

Этот граф можно перерисовать в таком виде:

Этот граф состоит из двух наборов вершин:

• X = {1, 4, 6, 7}
• Y = {2, 3, 5, 8}

Вершины множества X соединяются только с вершинами множества Y и наоборот. Кроме того, любые две вершины внутри одного множества не соединяются. Это удовлетворяет определению двудольного графа.

Следовательно, этот граф является двудольным.

Задача №2

Чему равно максимальное количество ребер в двудольном графе на 12 вершинах?

Известно, что максимально возможное число ребер в двудольном графе на 'n' вершин = (1/4) x n^2.

Подставим n = 12. Посчитаем максимальное количество ребер в двудольном графе на 12 вершинах:

=(1/4) x (12)^2

=(1/4) x 12 x 12

=36

Следовательно, максимальное количество ребер в двудольном графе на 12 вершинах = 36.

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты