Теория: Связанность графов

В теории графов много разных типологий и делений на виды. В этом уроке мы рассмотрим еще одну типологию и познакомимся с понятием связанности. Эти знания помогут эффективнее строить графы, особенно в тех задачах, когда речь идет о расстояниях.

Связный и разомкнутый граф

Граф называется связным, если можно проложить путь между каждой парой его вершин. Если хотя бы две вершины не соединены, граф называется несвязным или разомкнутым. Посмотрим на примере ниже:

Также в разговоре о связанности графов важен еще один термин — компонента графа. Это максимальный связный подграф, который нельзя сделать больше, не потеряв связанность при этом.

Вернемся к примеру выше и рассмотрим второй граф. Он разомкнутый, при этом в нем есть три связных подграфа. Например, нижняя часть треугольника — связный подграф, но не компонент. Другими словами, множество вершин компоненты такое, что для любых двух вершин из этого множества существует путь из одной в другую.

Компонента — это связный подграф, который настолько велик, насколько это возможно. Нет такой вершины, которую можно было бы добавить к нему, и чтобы он оставался связным. Также компонента — это связный подграф, который не содержится ни в каком другом связном подграфе.

У связного графа может быть только одна компонента. Компонента из одной вершины, называется изолированной вершиной.

Как и другие, связные графы можно делить на большее количество компонентов. Разберем, как это можно сделать.

Вершина и ребро разреза

У вершин и ребер есть два важных типа:

• Вершина разреза — это вершина, удаление которой разбивает граф на большее количество компонентов, чем было
• Ребро разреза — это ребро, которое при удалении разбивает граф на большее количество компонентов, чем было

Если удалить из связного графа вершину разреза или ребра разреза, то граф разъединится. Например:

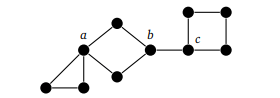
В этом графе вершины a, b и c — разрезанные, так как удаление любой из них приведет к разъединению графа. Ребро bc — разрезанное по той же причине. Других разрезанных вершин и разрезанных ребер в графе нет.

Разрезанные вершины и ребра действуют как «узкие места», когда речь идет о связности. Например, любой путь в графе выше от крайней левой до крайней правой вершины должен проходить через a, b, c и ребро bc.

Если удалить разрезанную вершину, это разобьет связный граф на две составляющие или больше. Например, удаление центра звезды разобьет вершину на множество компонентов. Удаление разрезанного ребра может разбить только связный граф только на две составляющие.

Расстояние

Промежуток между двумя вершинами графа называется расстоянием и показывает, насколько вершины удалены друг от друга.

Например, если обозначить расстояние между двумя вершинами d(u, v), значит, это длина кратчайшего пути между u и v в графе.

Посмотрим на этот граф:

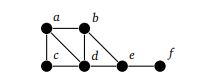
На приведенном ниже графике b, c и d находятся на расстоянии 1 от a. Вершина e находится на расстоянии 2 от a, а вершина f — на расстоянии 3 от a:

Кроме того, существует несколько путей из a в d, но длина самого короткого пути — 1, поэтому это и есть расстояние.

Выводы

В этом уроке мы познакомились с еще несколькими важными терминами из теории графов:

• Связный граф — граф, в котором можно проложить путь между каждой парой его вершин
• Разомкнутый граф — граф, в котором хотя бы две вершины не соединены
• Компонента — максимальный связный подграф, который нельзя сделать больше, не потеряв связанность при этом
• Вершина или ребро разреза — это вершина или ребро, удаление которых разбивает граф на большее количество компонентов, чем было