Существует много теорем, которые гарантируют наличие у графа гамильтонова цикла. При этом должно работать условие, что у графа есть определенные свойства. Одним из самых простых является условие Дирака, с котором мы познакомимся в этом уроке.
Как найти гамильтонов цикл с условием Дирака
Докажем наличие гамильтонова цикла в графе через теорему с условием Дирака. Допустим, если в простом графе с n ≥ 3 вершинами у каждой вершины степень не менее n/2, то у графа есть гамильтонов цикл.
Используем доказательство существования — пока каждая вершина смежна хотя бы с половиной вершин, у этого графа есть гамильтонов цикл. Этот способ показывает, что гамильтонов цикл существует, но не показывает, как его найти.
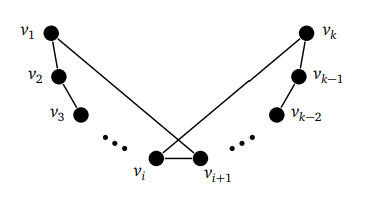
Найдем в графе путь stem:P максимальной длины. Пусть его вершины называются v1 , v2 , . . . . , vk. Мы покажем, что P можно превратить в цикл C.
Если v1 и vk смежные, то очевидно, что у нас есть цикл. В противном случае мы найдем цикл, показав, что на пути есть две смежные вершины, vi и vi+1. При этом v1 смежна с vi+1, а vk смежна с vi. Тогда мы получим цикл v1 , v2 , . . . . vi, vk, vk-1, ... vi+1, v1:
У конечных точек v1 и vk не может быть соседей, которые не лежат на P. В противном случае мы могли бы продлить путь до более длинного. Поэтому v1 — смежная с n/2 вершинами от v2 до vk-1.
Нам нужно, чтобы vk была смежной с вершиной на пути, которая предшествует одной из этих n/2 вершин. Если бы это было не так, то на пути было бы n/2 вершин, к которым vk не примыкает. Но это невозможно, так как у vk есть n/2 соседей, и все они должны лежать на пути.
Еще нам нужно показать, что только что найденный цикл C точно содержит все вершины графа. Предположим, что есть еще какая-то вершина w, которая не лежит в C. Поскольку v1 смежна с n/2 вершинами, все из которых лежат в P, более половины вершин графа лежат в P.
Так как deg(w) ≥ n/2, w должна быть смежной с какой-то вершиной vj из P. Но тогда мы могли бы создать более длинный путь, чем P. Для этого мы бы начали с вершины, которая следует сразу за vj в цикле C, прошли назад до vj, а затем в обход до w. Это невозможно, поэтому каждая вершина графа должна лежать на C, что делает C гамильтоновым циклом.
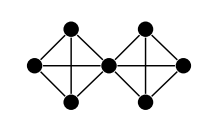
n/2 из теоремы не может быть уменьшено еще больше. Например, в приведенном ниже графе каждая вершина имеет степень не менее n/2 - 1, но гамильтонова цикла не существует из-за разрезанной вершины:
Выводы
В этом уроке мы разобрали теорему с условием Дикара, которая гарантирует наличие у графа гамильтонова цикла. Условие, что каждая вершина должна быть смежной по крайней мере с n/2 вершинами, гарантирует, что каждая вершина имеет довольно высокую степень. Это дает графу много ребер и нам большую свободу в попытках создать гамильтонов цикл.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
