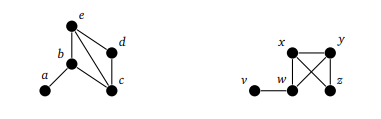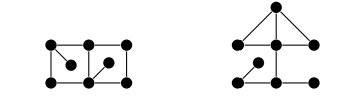Изоморфизм — Теория графов

• Что такое изоморфные графы
• Как доказать изоморфность графов
• Как доказать неизоморфность графов

Термин «изоморфизм» буквально означает «одинаковая форма». Он встречается во многих отраслях математики, в том числе в теории графов. В этом уроке мы узнаем, что означает этот термин. Вы научитесь определять изоморфные графы и доказывать свою точку зрения математически.

Что такое изоморфные графы

Два графа изоморфны, если это один и тот же граф, просто нарисованный или представленный по-другому. Например, на этом рисунке показаны два графа, которые изоморфны друг другу:

В обоих графах каждая вершина смежна с каждой другой вершиной, поэтому это две изоморфные копии K4.

Для такого простого примера несложно представить себе превращение одного графа в другой — надо просто переставить вершины местами. Но для графов с большим числом вершин такой подход не сработает.

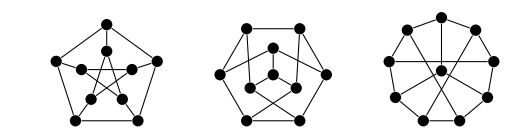
На самом деле довольно сложно показать, что большие графы изоморфны. Например, здесь все три графа изоморфны, но это неочевидно с первого взгляда:

В таких неочевидных случаях мы можем математически доказать, изоморфны графы друг другу или нет.

Как доказать изоморфность графов

Чтобы доказать изоморфность, рассмотрим ее определение:

Графы G и H изоморфны, в функции f: V(G) → V(H) соблюдаются два условия одновременно:

• v является смежным с w в G
• f (v) является смежным с f (w) в H

Другими словами, два графа считаются изоморфными, если мы можем идеально сопоставить вершины одного графа с вершинами другого. При этом смежность тоже должна совпадать:

• Если две вершины были смежными в первом графе, во втором они тоже должны быть смежными
• Если две вершины не были смежными в первом графе, во втором они тоже не должны быть смежными

Попробуем применить это определение на практике и доказать изоморфность этих графов:

Для этого мы сопоставляем вершины следующим образом:

• a ↔ v
• b ↔ w
• c ↔ x
• d ↔ z
• e ↔ y

Так это выглядит в виде функции:

• f(a) = v
• f(b) = w
• f(c) = x
• f(d) = z
• f(e) = y

С вершинами разобрались, осталось проверить, все ли ребра совпадают:

• Возьмем ребро ab в первом графе
• Вспоминаем, что вершины a и b сопоставлены с v и w
• Проверяем, есть ли ребро vw во втором графе
• Такое ребро есть, так что можно идти дальше

Таким же образом проверяем не-ребра:

• Посмотрим на первый граф и выясним, что на нем нет ребра от a до e
• Вспоминаем, что вершины a и e сопоставлены с v и y
• Проверяем, есть ли ребро vy во втором графе
• Такого ребра нет, так что можно идти дальше

Эта проверка может показать долгой и утомительной, но таким образом можно точно проверить все ребра и не-ребра.

Эту работу можно ускорить с помощью алгоритмов графов, но это отдельная сфера математики, о которой пока мы не будем говорить подробно.

Как доказать неизоморфность графов

Как мы увидели на примере выше, изоморфность доказать не всегда легко. С другой стороны, доказать неизоморфность двух графов обычно проще — нужно найти свойство, которое эти два графа не разделяют.

Например, два графа могут отличаться такими свойствами:

• Разное количество вершин или ребер
• Разное количество компонент
• Степени вершин в каждом графе
• Содержание абсолютно одинаковых подграфов

Чтобы лучше понять эти свойства, рассмотрим такой пример:

В этом примере графы имеют такие свойства:

• Одинаковое количество вершин и ребер
• Одна компонента в обоих случаях
• По две вершины степени 1, три вершины степени 2, две вершины степени 3 и одной вершине степени 4

Таким образом, первые три свойства не помогают. Однако нам на помощь приходит четвертое свойство: в первом графе нет треугольника-подграфа, а во втором — он есть.

Существует множество других возможностей доказать неизоморфность. Иногда для этого требуется немного творчества.

Например, вот эти графы неизоморфны:

Обратите внимание, что у них одинаковое количество вершин и ребер, степени почти всех вершин тоже одинаковы. Определим, в чем разница между ними. Второй граф содержит вершину степени 3, смежную с двумя вершинами степени 1 — в первом графе это не так.

К этому же примеру можно подойти по-другому:

1. На первом графе есть два пути длиной в пять вершин:
   • Прямой путь по горизонтали
   • Путь справа налево с поворотом вверх
2. На втором графе пути другие:
   • Прямой путь по горизонтали в пять вершин
   • Путь в три вершины слева направо с поворотом вверх
   • Путь в три вершины справа налево с поворотом вверх

В этом уроке мы разобрали изоморфизм в теории графов. Теперь вы умеете доказывать изормфность и неизоморфность графов даже в тех случаях, когда это неочевидно с первого взгляда.

Самостоятельная работа

Задача №1

Являются ли следующие два графа изоморфными?

Оба графа имеют 6 вершин, 9 ребер. Последовательность степеней одинакова. Однако во втором графе есть цепь длины 3, а минимальная длина любой цепи в первом графе равна 4. Следовательно, данные графы не изоморфны.

Задача №2

Являются ли следующие два графа изоморфными?

Проверим необходимые условия. Начнем с условия 1:

• Количество вершин в графе — G1 = 4
• Количество вершин в графе — G2 = 4

Здесь оба графа G1 и G2 имеют одинаковое количество вершин. Таким образом, условие 1 удовлетворяется.

Проверим условие 2:

• Количество ребер в графе G1 = 5
• Количество ребер в графе G2 = 6

Здесь оба графа G1 и G2 имеют разное количество ребер. Таким образом, условие 2 нарушается.

Поскольку условие 2 нарушается, данные графы не могут быть изоморфными. G1 и G2 не являются изоморфными графами.

Задача №3

Какие из следующих графов изоморфны?

Шаг 1. Проверим необходимые условия. Начнем с условия 1:

• Количество вершин в графе G1 = 4
• Количество вершин в графе G2 = 4
• Количество вершин в графе G3 = 4

Здесь все графы G1, G2 и G3 имеют одинаковое количество вершин. Таким образом, условие 1 удовлетворяется.

Шаг 2. Проверим условие 2:

• Количество ребер в графе G1 = 5
• Количество ребер в графе G2 = 5
• Количество ребер в графе G3 = 4

Здесь графы G1 и G2 имеют одинаковое количество ребер. Таким образом, условие 2 удовлетворяется для графов G1 и G2. Однако графы (G1, G2) и G3 имеют разное количество ребер. Значит, условие 2 нарушается для графов (G1, G2) и G3.

Поскольку условие 2 нарушается для графов (G1, G2) и G3, они не могут быть изоморфными. G3 не изоморфен ни G1, ни G2.

Так как условие 2 удовлетворяется для графов G1 и G2, то они могут быть изоморфны. G1 может быть изоморфен G2.

Шаг 3. Теперь продолжим проверку для графов G1 и G2. Проверим условие 3:

• Последовательность степеней графа G1 = { 2 , 2 , 3 , 3 }
• Последовательность степеней графа G2 = { 2 , 2 , 3 , 3 }

Здесь оба графа G1 и G2 имеют одинаковую последовательность степеней. Таким образом, условие 3 удовлетворяется.

Шаг 4. Проверим условие 4:

• Оба графа содержат два цикла длиной 3 каждый, образованные вершинами со степенями { 2 , 3 , 3 }.

Это означает, что оба графа G1 и G2 имеют одинаковые циклы. Таким образом, условие 4 удовлетворяется.

Таким образом, все 4 необходимых условия выполнены. Значит, графы G1 и G2 могут быть изоморфны.

Шаг 5. Теперь давайте проверим достаточное условие. Мы знаем, что два графа обязательно изоморфны тогда и только тогда, когда изоморфны их комплементарные графы.

Итак давайте построим графы дополнения графов G1 и G2:

Очевидно, что дополняющие графы G1 и G2 изоморфны. Графы G1 и G2 являются изоморфными графами.

Задача №4

Являются ли следующие два графа изоморфными?

Шаг 1. Проверим необходимые условия. Начнем с условия 1:

• Количество вершин в графе G1 = 8
• Количество вершин в графе G2 = 8

Здесь оба графа G1 и G2 имеют одинаковое количество вершин. Таким образом, условие 1 удовлетворяется.

Шаг 2. Проверим условие 2:

• Количество ребер в графе G1 = 10
• Количество ребер в графе G2 = 10

Здесь оба графа G1 и G2 имеют одинаковое количество ребер. Таким образом, условие 2 удовлетворяется.

Шаг 3. Проверим условие 3:

• Последовательность степеней графа G1 = { 2 , 2 , 2 , 2 , 2 , 3 , 3 , 3 , 3 }
• Последовательность степеней графа G2 = { 2 , 2 , 2 , 2 , 2 , 3 , 3 , 3 , 3 }

Здесь оба графа G1 и G2 имеют одинаковую последовательность степеней. Таким образом, условие 3 удовлетворяется.

Шаг 4. Проверим условие 4:

• В графе G1 вершины степени 3 образуют цикл длины 4
• В графе G2 вершины степени 3 не образуют 4-цикл, так как вершины не являются смежными

Здесь оба графа G1 и G2 не содержат одинаковых циклов. Значит, условие 4 нарушается.

Поскольку условие 4 нарушается, данные графы не могут быть изоморфными. G1 и G2 не являются изоморфными графами.

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты