В этом уроке мы разберем знаменитую в теории графов теорему Менгера, которая помогает перекрыть путь от одной вершины к другой.
Теорема Менгера
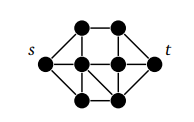
Прежде чем разобраться с теоремой Менгера, представим, что нам даны две вершины в графе. Мы хотим узнать, сколько вершин нужно удалить, чтобы разделить эти две вершины — сделать невозможным переход от одной к другой. Например, в приведенном ниже графе нам нужно удалить три вершины, чтобы сделать невозможным переход от s к t:
Еще нас интересует, сколько существует маршрутов из s в t, у которых нет общих вершин кроме самих s и t. В приведенном выше графе существует множество маршрутов из s в t. Мы можем найти три маршрута, у которых нет общих вершин. Мы можем пройти через вершину, низ или середину.
Число три совпадает с количеством вершин, которые нужно удалить, чтобы отделить s от t. Это не совпадение, а пример теоремы Менгера.
Теорема Менгера: пусть s и t — несмежные вершины в некотором графе. Минимальное число вершин, которые нужно удалить из графа, чтобы из s в t было невозможно попасть, равно максимальному числу путей из s в t, не имеющих общих вершин, кроме s и t.
Если у нас есть набор вершин, которые отделяют s от t, то этот набор должен содержать вершину каждого пути между s и t. А если мы рассматриваем непересекающиеся пути от s к t, то никакая вершина не может удалить два пути одновременно. Получается, что минимальное количество вершин, которое необходимо для отделения s от t такое же, как и максимальное количество непересекающихся путей от s к t. Довольно сложно пойти в другом направлении и показать, что оно не больше.
Это еще одна теорема, подобная теореме Кенига-Эгервари, где минимизация одной величины дает ответ на максимум другой. В теореме Кенига-Эгервари речь шла о том, что минимальное вершинное покрытие приводит к максимальному соответствию того же размера.
Здесь у минимального разделяющего множества вершин тот же размер, что и максимальное число вершинно-разделительных путей. Теорему Кенига-Эгервари можно использовать, чтобы доказать теорему Менгера и наоборот. Эти теоремы в некотором смысле эквивалентны.
Существует также краевая версия теоремы Менгера. Она формулируется так:
Максимальное количество путей между s и t равно минимальное количество ребер, которые нужно удалить, чтобы отделить s от t. При этом у s и t нет общих ребер
Теорема Менгера приводит к следующей характеристике связности:
Граф будет k-связным тогда и только тогда, когда между любой парой вершин есть не менее k путей, у которых нет общих вершин, кроме своих конечных точек
Выводы
В этом уроке мы познакомились с теоремой Менгера. Теперь вы умеете вычислять, сколько вершин нужно удалить, чтобы разделить две вершины. Так вы сможете упрощать и ускорять свою работу с графами, разделяя большие и сложные графы на отдельные подграфы.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
