В этом уроке мы разберем, что такое поточная сеть. Вы узнаете, как строятся такие сети и как диграфы помогают в этом.
Как строится поточная сеть
Представим, что у нас есть диграф и две вершины — источник и сток. У каждого ребра есть вес, который называется его пропускной способностью. Нам нужно пропустить как можно больше материала через диграф от источника к стоку. Это называется потоком, а взвешенный диграф — сетью. Таким образом мы строим сетевой поток.
Например, источник — это a, а сток — h:
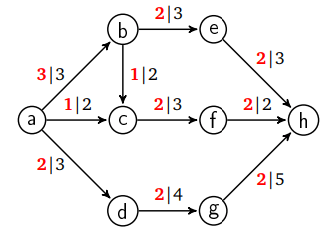
Первое число, выделенное красным на каждом ребре — это значение потока, а второе — пропускная способность. В этом случае поток не оптимальный, так как через сеть можно пропустить больше вещей, чем 6 единиц.
Количество потока на ребре не может превышать его пропускную способность. Еще общее количество потока в вершину должно быть равно общему количеству потока из этой вершины, за исключением источника и стока. В итоге поток проходит через вершины, которые не создают и не потребляют поток.
Общее объем потока, который проходит через сеть, называется величиной потока. Это количество можно найти, если посчитать:
- Общий поток, который выходит из источника
- Общий поток, который входит в сток
Многие реальные проблемы можно смоделировать с помощью сетей потоков. Например, источник — это место, где мы добываем сырье. Его нужно доставить на завод — сток. Края — это различные маршруты, по которым мы можем отправить сырье, а мощность — сколько материала можно доставить по этим маршрутам.
Если предположить, что транспортная сеть — это ограничивающий фактор, то нас интересует, сколько сырья мы можем доставить на фабрику.
Многие несвязанные проблемы теории графов можно преобразовать в проблемы сетевых потоков.
Теорема о максимальном потоке и минимальном разрезе
С потоками тесно связаны разрезы. Разрез — это набор ребер, удаление которых делает невозможным путь от источника к стоку. Нас интересует сумма мощностей ребер в разрезах. Например, ниже показан разрез из ребер be, bc, ac и d g. Его общая емкость равна 3 + 2 + 2 + 4 = 11:
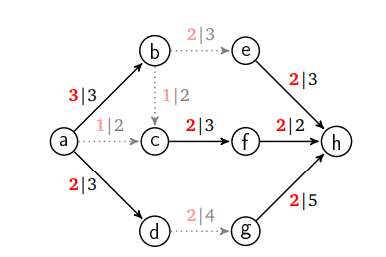
Между потоками и разрезами, а также не пересекающимися путями между вершинами и отсекающими две вершины множествами из теоремы Менгера есть сходства. Разберем взаимосвязь между потоками и разрезами в сети через теорему:
В любой сети ценность каждого потока меньше или равна пропускной способности каждого разреза
Докажем эту теорему. При любом разрезе C каждый поток должен проходить хотя бы через одно ребро C. Если бы это было не так, то C не был бы разрезом, потому что существовал бы способ добраться от источника до стока по этому потоку. Поскольку поток должен проходить хотя бы через некоторые ребра C, его величина не может превышать суммарную мощность этих ребер.
Если мы можем найти поток и разрез одинакового размера, то мы знаем, что наш поток — максимальный, а разрез минимальный.
И у нас есть сетевой аналог теоремы Кенига-Эгервари — теорема Max-flow min-cut:
В любой сети максимальное значение потока равно минимальному значению разреза
Например, на схеме ниже изображен максимальный поток:
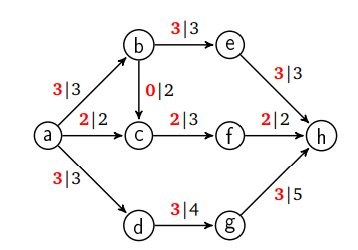
Всего по сети движется восемь единиц потока. Это видно, если сложить поток из источника и поток в сток. Минимальный разрез в этой сети состоит из ребер a → b, a → c и a → d. Их общая пропускная способность равна 3 + 2 + 3 = 8. Поскольку у нас есть поток и разрез одинакового размера, наш поток максимален, а разрез минимален.
Итоги курса
На этом курсе вы познакомились с большинством важных тем из теории графов. Чтобы действительно усвоить материал, не забывайте выполнять все задания и постоянно практиковаться.
В этом курсе все важные темы мы изучили на вводном уровне. Этого уже хватит, чтобы вы смогли применять теорию графов к реальным проблемам. Но если вы хотите погрузиться в теорию графов подробнее, вы можете изучить дополнительную литературу:
- Graph Theory: A Problem Oriented Approach by Daniel A. Marcus, Mathematical Association of America, 2008
- Introduction to Graph Theory, 2nd ed. by Douglas B. West, Prentice Hall, 2001
- Introduction to Graph Theory by Gary Chartrand and Ping Zhang, Dover Publications, 2012
- Graph Theory and Its Applications, 2nd ed. by Jonathan Gross and Jay Yellen, Chapman and Hall/CRC 2005
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
