Нотации — Теория графов

• Что такое простой граф
• Матричная нотация простых графов
  • Матрица смежности
  • Матрица инцидентности
• Выводы

В этом уроке мы переходим от теории к практике. Мы будем работать на примерах и рассмотрим графы со специфическими свойствами. Вы узнаете больше о простых графах, матрицах и других базовых понятиях теории графов.

Что такое простой граф

Простыми называются графы с такими свойствами:

• В них нет параллельных ребер — между вершинами лежит только по одному ребру
• В них нет петель — нет ребер, которые начинаются и заканчиваются в одной и той же вершине

Рассмотрим пример визуализации простого графа:

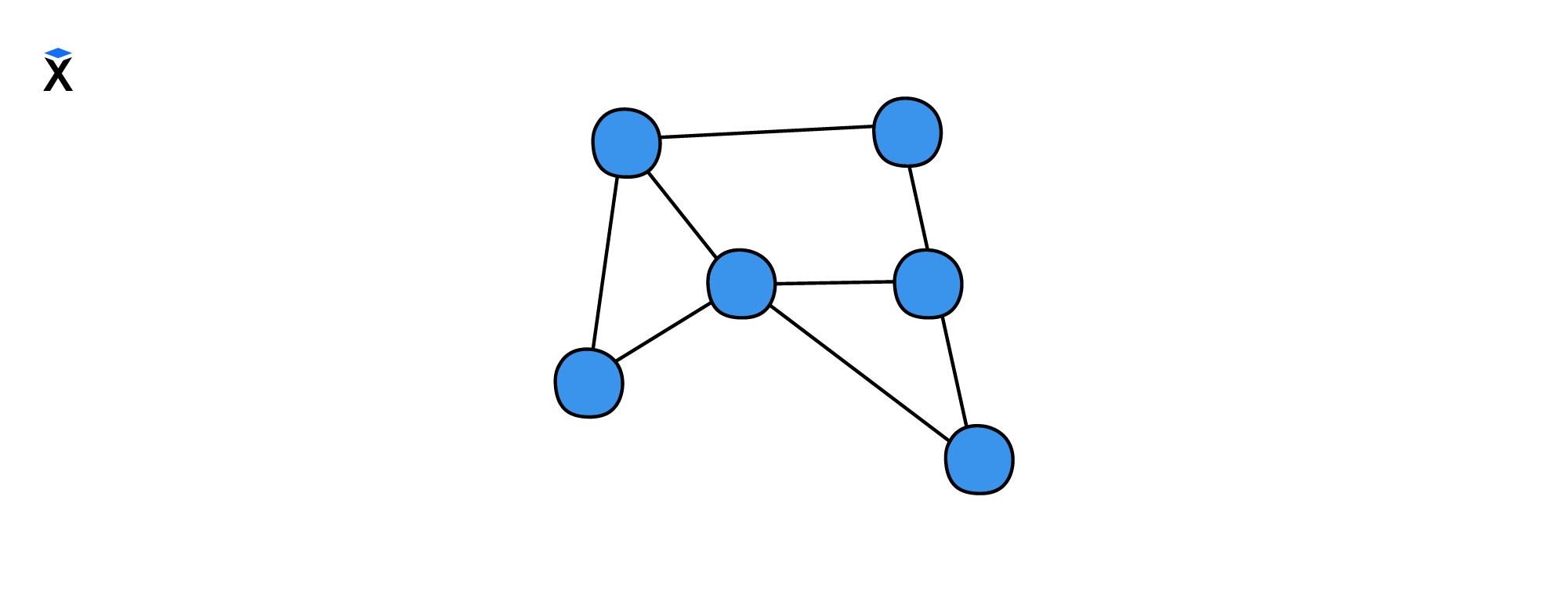
Такие визуальные представления графа содержат массу полезной информации, но пока она нам недоступна. Чтобы раскрыть эти данные в удобном виде, нужно научиться описывать граф.

Для начала обозначим этот граф, чтобы лучше понять открывающую формулу G = <V,E>.

У наших вершин отсутствуют метки, поэтому присвоим любой случайной вершине метку A. Затем пройдемся по графу, обозначая каждую вершину буквенно-цифровым символом. Пока ничего сложного — мы просто присвоили символы вершинам нашего графа:

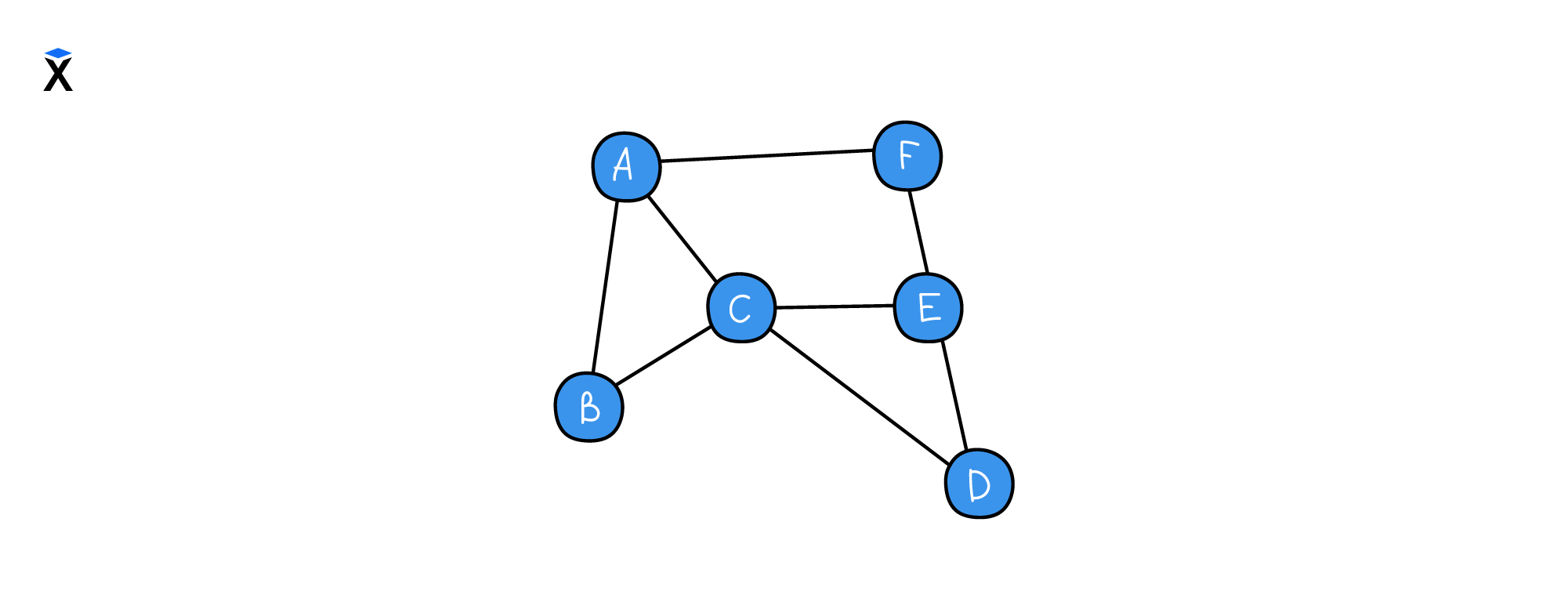
Теперь построим числовую нотацию графа. Для этого мы создадим два набора обозначений:

1. Вершины графа. Здесь все достаточно просто — это набор символов A, B, C, D, E, F
2. Ребра графа. Ребро — это то, что соединяет две вершины. Отсюда следует, что ребро можно представить через две вершины, которые оно соединяет. Другими словами, множество ребер содержит список координатно-подобных вершин. Например, первое ребро между вершинами A и B обозначается как AB

Запишем представление множества для остальной части графа:

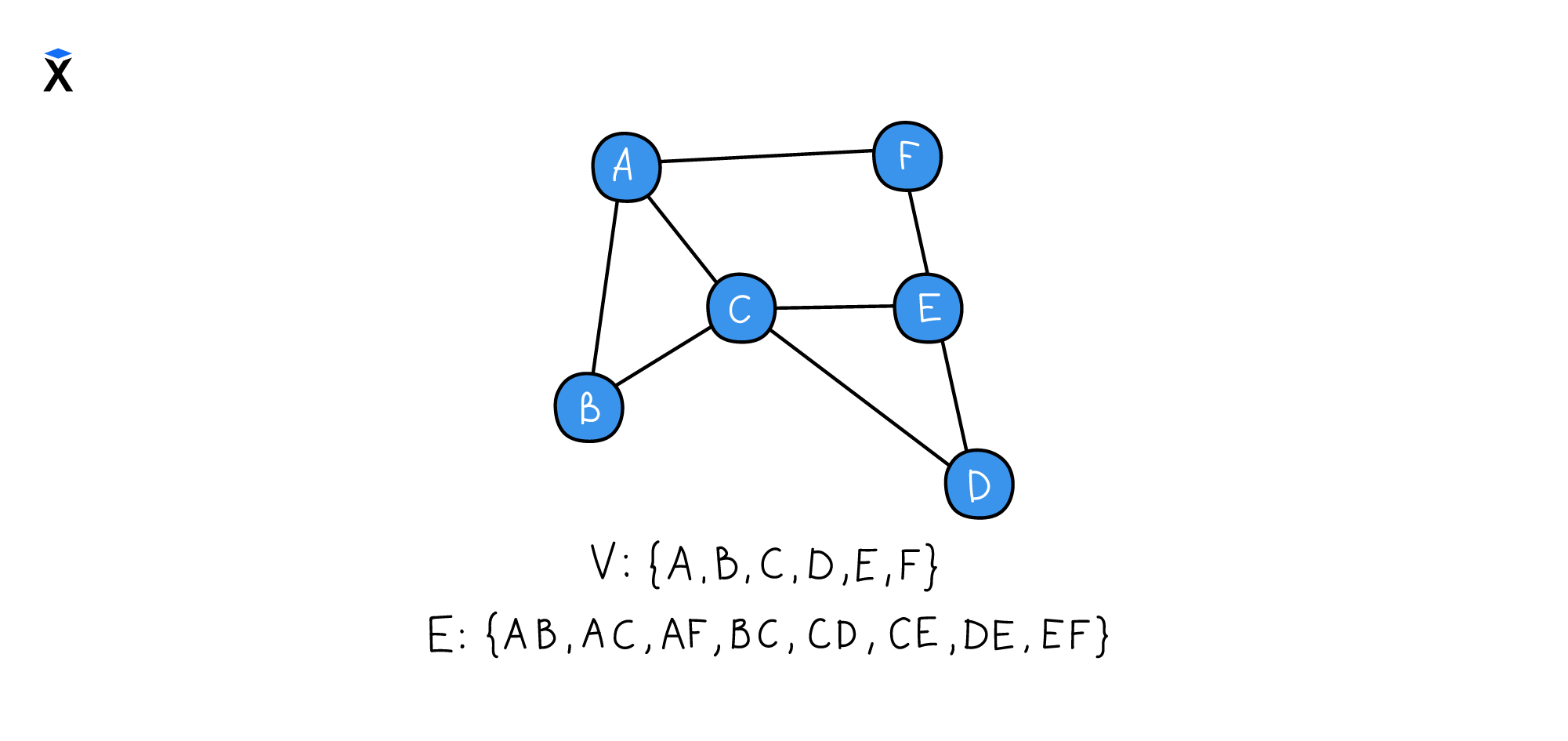
Как показано на рисунке выше, стандартная нотация для графа G может быть идеально описана двумя отдельными наборами обозначений: один для вершин, а другой — для ребер.

Теперь представим, что нам нужно передать граф на обработку компьютеру. Как передать ему обозначения? В текущем виде это было бы неудобно, поэтому воспользуемся другим методом — матричной нотацией.

Матричная нотация простых графов

Компьютеры лучше справляются с числами, чем с распознаванием изображений. Именно поэтому спецификации графа чаще всего передаются компьютеру в матричной форме.

В промышленности практикуются два основных типа:

• Матрицы смежности
• Матрицы инцидентности

Рассмотрим два этих метода и обозначим наш граф обоими способами.

Матрица смежности

Матрица смежности основана на вершинах, смежных друг с другом — еще их называют связанными или соседними. Другими словами, матрица смежности описывает, являются ли две вершины смежными (1) или нет (0). Каждый элемент в такой матрице — это просто булево число, описывающее связность.

Вернемся к примеру —графу G с множеством вершин V и множеством ребер E. В матрице смежности этот граф преобразуется в матрицу размера V^2. Строки и столбцы обозначены одним и тем же единственным набором вершин для любого графа G. Внутри матрицы мы находим либо 0, либо 1. В этом случае единица означает две смежные вершины:

• Первая обозначена в строке
• Вторая обозначена в в столбце

Таким образом, матрица смежности — это граф в виде матрицы, в которой основное внимание уделяется смежным вершинам. Давайте расшифруем наш граф в виде матрицы смежности:

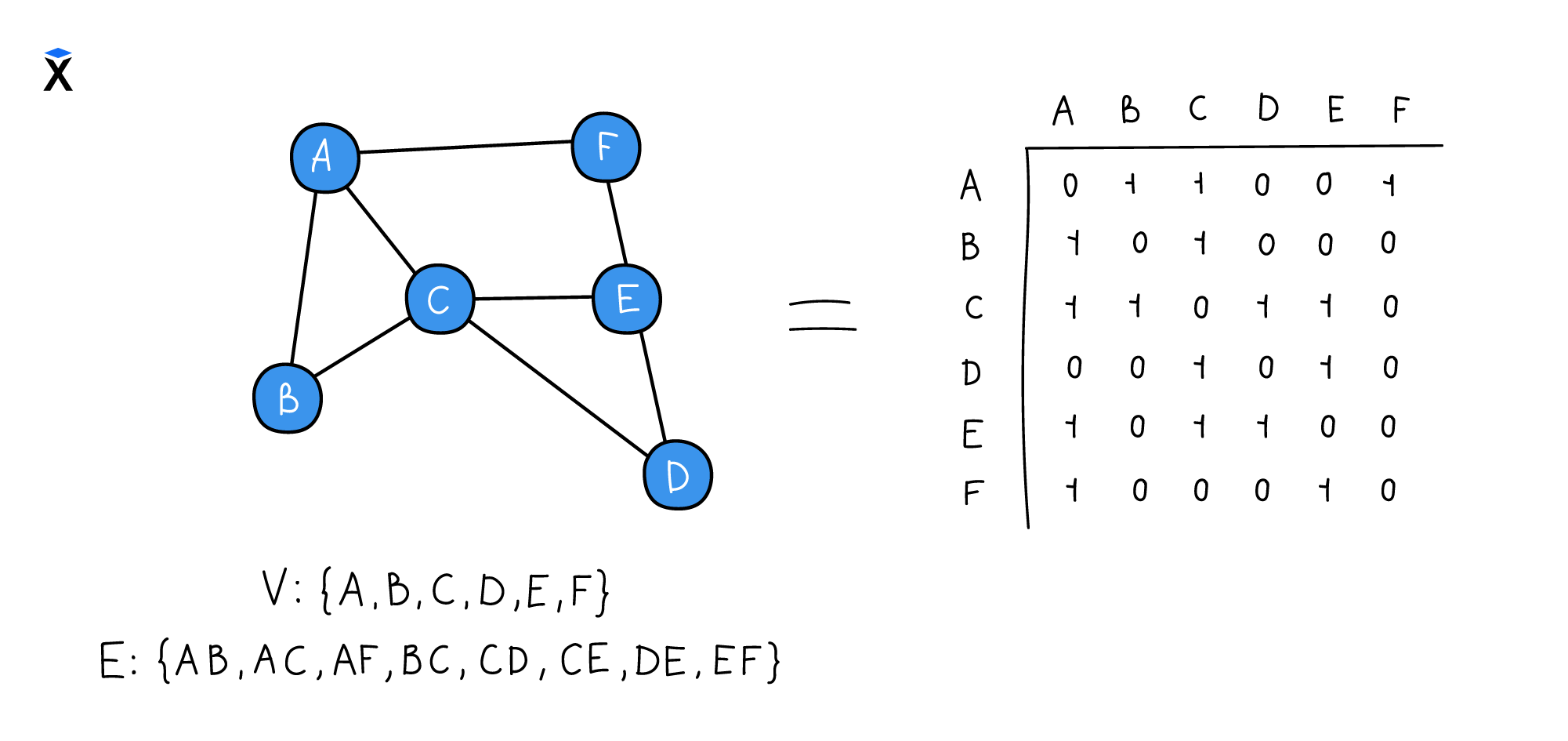
Матрица инцидентности

Второй распространенный синтаксис для преобразования графов в матрицы — это матрица инцидентности.

В ней граф G с множеством вершин V и множеством ребер E преобразуется в матрицу размером V на E. Строки и столбцы обозначаются как вершины и ребра соответственно. Внутри матрицы мы снова видим, что все элементы обозначены либо как 0, либо как 1 — больше булевых чисел. На этот раз единица означает связь между вершиной в строке и ребром в столбце.

Интересное свойство матриц инцидентности: при сложении всех элементов в столбце всегда получается два. Это закономерно, потому что любое ребро в простом графе имеет только две вершины, соединенные с ним.

Запишем наш пример графа в виде матрицы инцидентности:

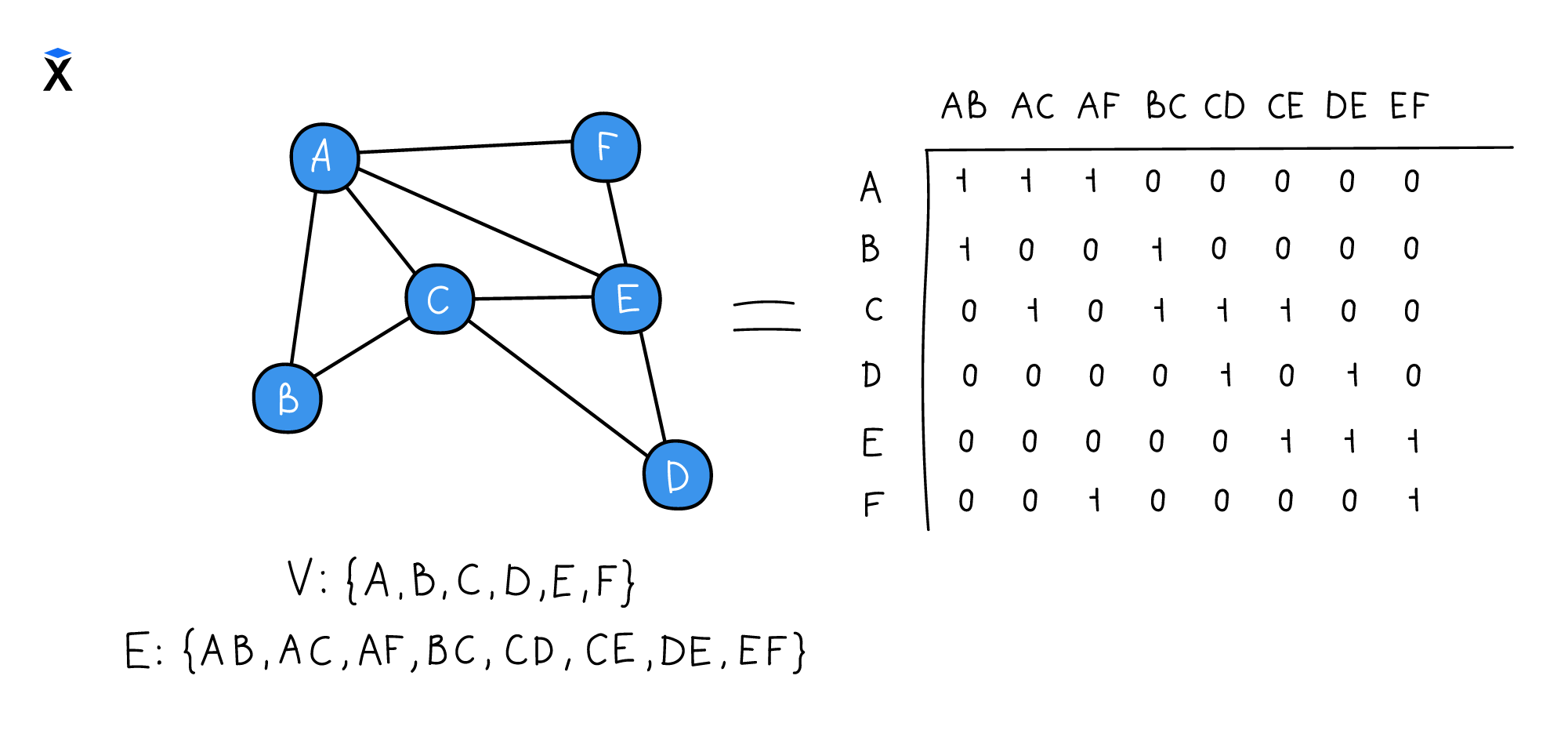
Сравнивая обе матричные нотации, можно вывести несколько дифференциалов:

• В большинстве случаев, ребер всегда больше, чем вершин, поэтому матрицы смежности имеют меньше столбцов, чем матрицы инцидентности
• По той же причине матрицы смежности более разрежены — от 0 до 1. Можно предположить, что они менее информативны на элемент матрицы
• Матрицы смежности всегда имеют форму квадрата, а матрицы инцидентности — форму прямоугольника

Ключевое различие заключается в обозначениях:

• В первой матрице вершины представлены и в строках, и в столбцах
• Во второй матрице вершины представлены только в строках, а столбцы обозначают ребра

Выводы

В этом уроке мы изучили простые графы и матрицы смежности. С этими знаниями вы сможете перейти к изучению различных типов графов, разберетесь с более запутанными графами. В итоге эта тема поможет разобраться в одной интересных областей теории графов — теории сетей.

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты