В этом уроке мы покажем, как работать с графами на примере задачи. Представим, что нам нужно найти кратчайший маршрут на складе для комплектации товаров. При этом не везде можно ездить, а пересечение коридоров на складе разрешено только в обозначенных «поворотных точках». Кроме того, направление движения должно соответствовать указанному для каждого коридора.
Формулируем задачу в теории графов
Сформулируем данную задачу, как оптимизационную в теории графов. Все пункты приема на складе образуют узел в графе, где ребра — разрешенные коридоры и расстояния между узлами. Начнем с упрощенного примера:
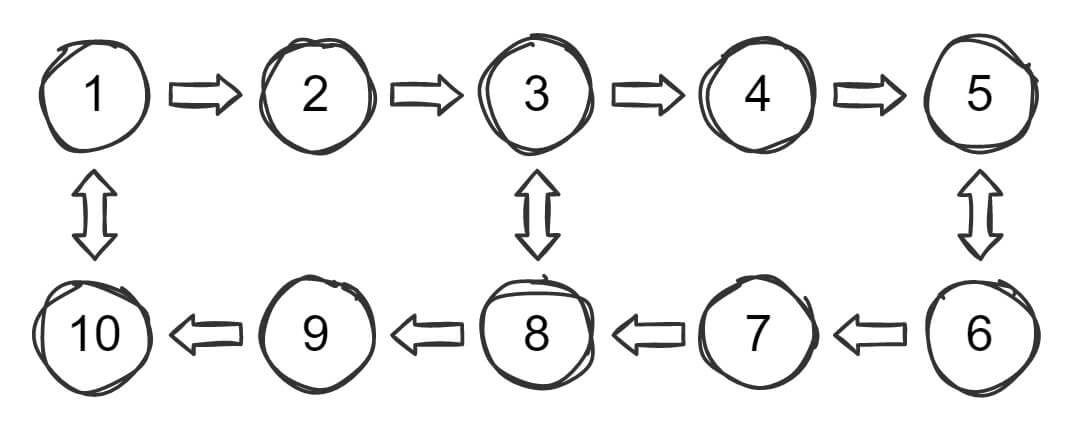
Граф выше — это два коридора с пятью пунктами приема в каждом коридоре. Все пункты — узлы на графе, с адресом в диапазоне от одного до десяти. Стрелки указывают разрешенное направление движения, а двойные стрелки указывают, что вы можете ехать в любую сторону.
Если мы можем представить маршруты движения в виде графа, значит, мы можем использовать математические методы, известные из теории графов. Это поможет найти оптимальный маршрут движения между узлами — пунктами.
Приведенный выше пример графа можно описать с помощью матрицы смежности:
-
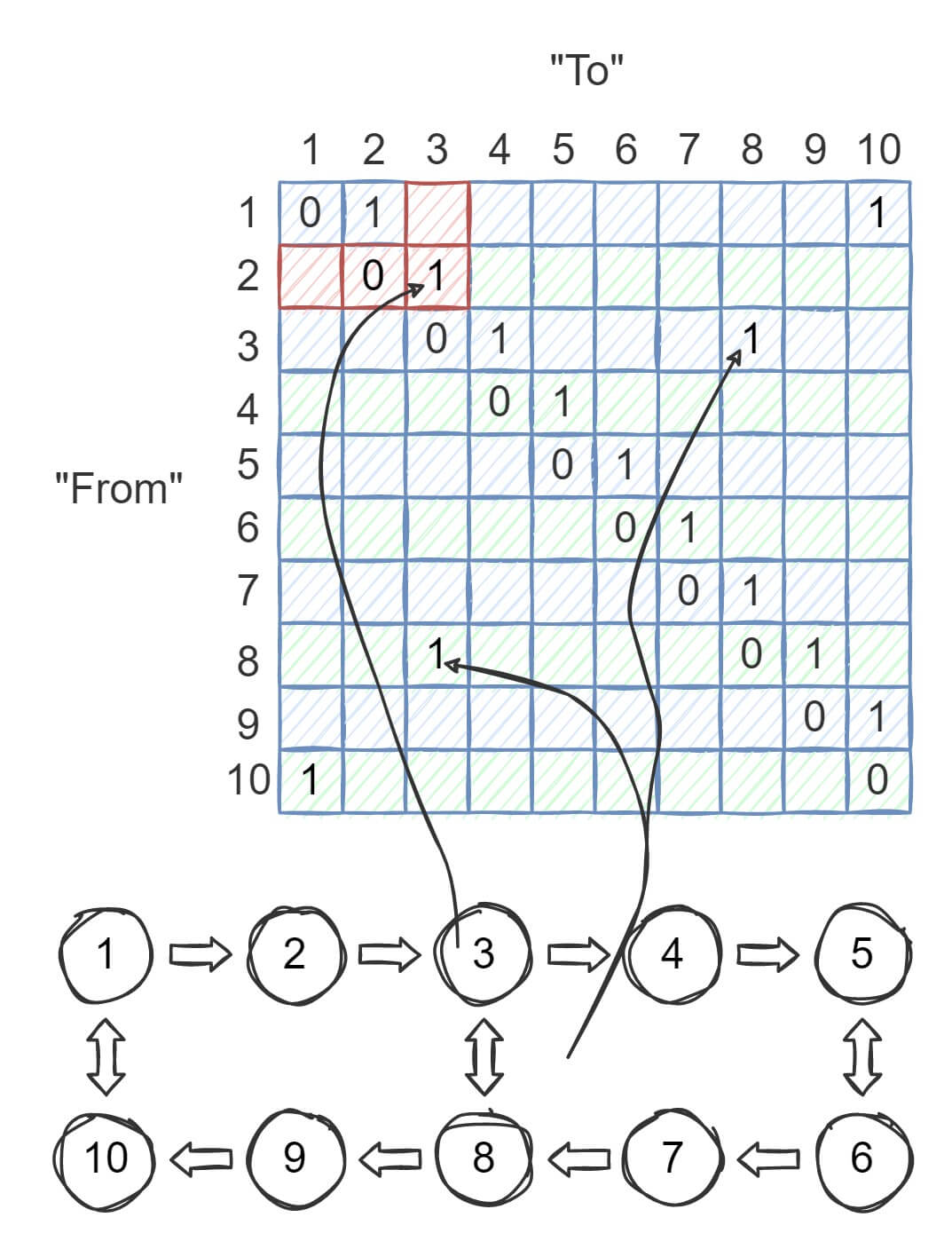
Пример 1: разрешено перемещаться из узла в , но не из в . На это указывает единица в матрице смежности справа
-
Пример 2: разрешено ехать как из узла в , так и из в , на что опять же указывают единица в матрице смежности. В данном случае симметрична
Вернемся к проблеме со складом
Реальный склад больше и сложнее, чем приведенный выше пример. Однако основные принципы работы с графиками остаются теми же. Чтобы упростить реальную задачу, представим небольшой склад:
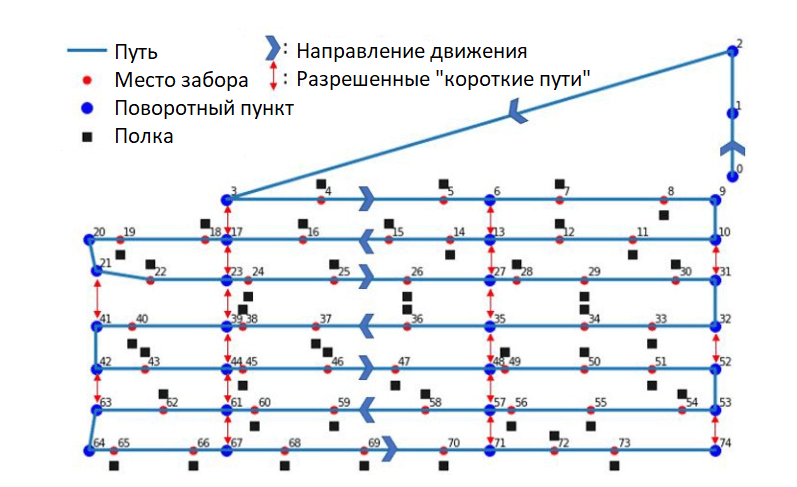
Рассмотрим подробнее эту сложную схему:
-
Здесь показано общее количество полок (точек комплектации) — включена каждая 50-я полка, они отмечены черными квадратами
-
Всем точкам подбора присвоен адрес (номер узла) от 1-74
-
Стрелками показаны разрешенные направления движения, поворотные точки и короткие пути между коридорами
Опишем этот граф в виде матрицы смежности. Еще включим в нее расстояние между различными узлами, так как нам нужно найти оптимальный маршрут:
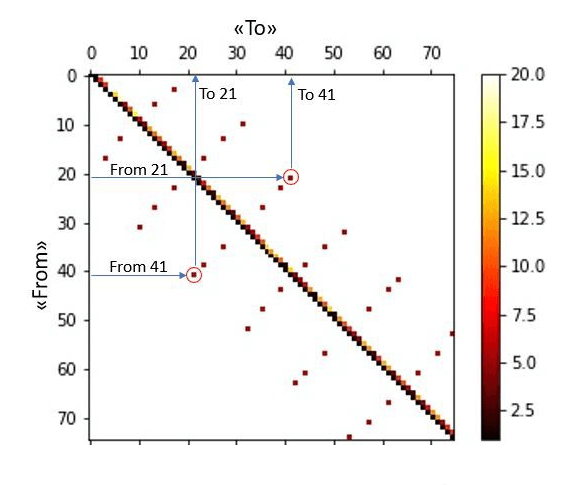
В этой матрице снова указаны все ограничения:
-
Разрешенное направление движения
-
Разрешенные короткие пути
-
Расстояние между узлами
Также на матрице мы четко видим короткий путь между узлами и . Белые области матрицы представляют неразрешенные пути, обозначенные через бесконечное расстояние между этими узлами.
Оптимизация графов — это хорошо известная область математики, которая уже успела прийти к нескольким методам и алгоритмам, которые могут решить этот тип проблемы. В этом примере мы основывали решение на алгоритме Флойда-Уоршалла. Он помогает искать кратчайшие пути во взвешенном графе, и эту темы мы рассмотрим подробнее по ходу курса. Одно выполнение алгоритма позволяет найти длины — суммированные веса кратчайших путей между всеми парами узлов. Хотя он не возвращает подробностей о самих путях, их можно восстановить с помощью простых модификаций алгоритма.
Абстрактное представление склада в виде графа, не решает нашу задачу. При этом благодаря графу можно использовать математическую основу и алгоритмы из теории графов, чтобы решить задачу.
Существует несколько методов и алгоритмов, которые могут решить этот тип задачи. В данном примере мы использовали алгоритм Флойда-Уоршалла — он помогает искать кратчайшие пути во взвешенном графе. Его мы разберем в других уроках этого курса.
С помощью одного действия в алгоритме можно найти длины кратчайших путей между всеми парами узлов. При этом мы не узнаем подробности о каждом пути, а сможем восстановить их с помощью простых модификаций алгоритма.
Если дать этому алгоритму в качестве входных данных список заказов на сборку, в котором перечислены необходимые для комплектации товары, то можно получить оптимальный маршрут.
Например, визуализируем результаты для короткого списка комплектации:
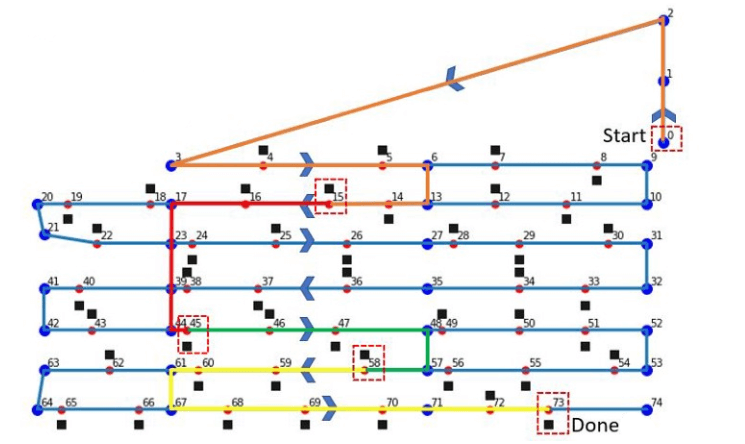
Начнем с узла и заберем товары в узлах и . Алгоритм находит кратчайший допустимый маршрут между этими точками путем вычисления матрицы расстояний . Затем ее можно использовать, чтобы определить общее расстояние между всеми узлами в списке комплектации:
Общее расстояние — это самый короткий путь
Алгоритм протестировал несколько списков подбора в качестве входных данных и проверил предложенные маршруты движения и рассчитанное расстояние, и нашел оптимальный маршрут во всех случаях. Алгоритм соблюдает все наложенные ограничения.
Выводы
В этом уроке вы увидели, как работать с графами на примере задачи. Мы нашли кратчайший маршрут на складе для комплектации товаров и использовали для этого матрицы смежности и алгоритм Флойда-Уоршалла.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
- Статья «Как учиться и справляться с негативными мыслями»
- Статья «Ловушки обучения»
- Статья «Сложные простые задачи по программированию»
- Вебинар «Как самостоятельно учиться»
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
