Алгоритм Дейкстры — Теория графов

Алгоритм Дейкстры находит кратчайшие пути между всеми вершинами графа и их длину. Он используется в ряде реальных приложений, таких как маршрутизация сетевых пакетов.

Разберем, как он работает. Предположим, начальная вершина называется . Алгоритм помечает вершину двумя параметрами:

С помощью алгоритма Дейкстры можно постоянно улучшать стоимость по мере нахождения лучших путей к v. Для этого нужно работать в следующем порядке:

Шаг 1. Устанавливаем метки стоимости каждого соседа на стоимость ребра от до него и метку вершины на . Помечаем как искомое. Эта метка будет означать, что мы не будем посещать ее снова.

Шаг 2. Выбираем помеченную вершину с наименьшей стоимостью и развиваем связи по своему усмотрению. Смотрим каждого соседа . Если сосед не помечен, то мы помечаем его стоимостью плюс вес ребра к нему от . Его вершинной меткой становится .

Если сосед уже помечен, то мы сравниваем его текущую стоимость метки с плюс вес ребра к нему от . Если это не лучше, чем текущая стоимость метки соседа, то мы больше ничего не делаем с этой вершиной. В противном случае мы обновляем стоимость метки на эту новую стоимость и обновляем метку соседней вершины на . Мы повторяем это для каждого незамеченного соседа v и затем помечаем саму v как искомую.

Шаг 3. Продолжаем на каждом шаге выбирать немаркированную вершину с наименьшей стоимостью и обновлять метки ее соседей, как на втором шаге.

Шаг 4. Завершаем алгоритм, когда вершина с наименьшей стоимостью является вершиной назначения. Эта стоимость — общая стоимость кратчайшего пути. Затем мы используем метки вершин для поиска пути от начала до места назначения.

Рассмотрим работу алгоритма на примере, чтобы лучше понять весь его процесс.

Чтобы увидеть, как работает алгоритм Дейкстры, рассмотрим пример ниже. В нем мы ищем кратчайший путь из вершины в вершину :

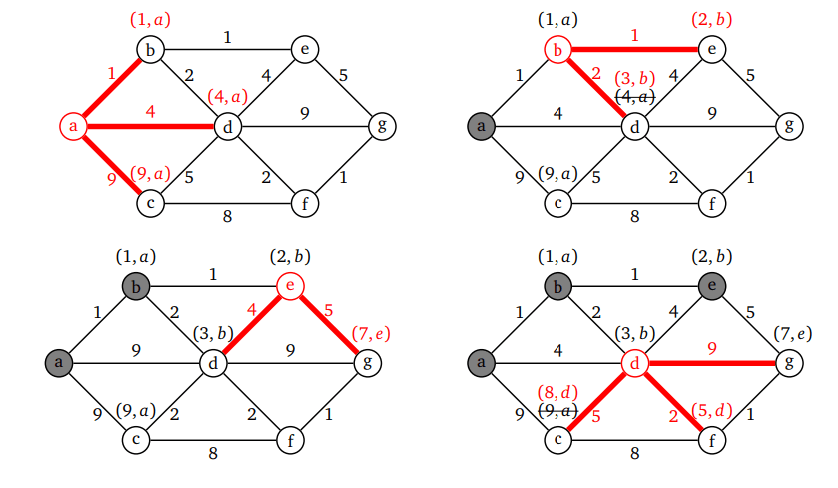
Шаг 1. Мы начинаем с вершины , посещаем каждую из соседних вершин и помечаем их стоимостью от , вместе с . Так мы обозначаем, что нашли их через вершину . Затем мы помечаем как искомое (серым цветом), что означает, что мы больше не будем его посещать.

Шаг 2. Далее мы выбираем соседа , которого пометили наименьшей стоимостью — вершина . Посещаем ее соседей.

Мы можем добраться до из с общей стоимостью . Поскольку добраться из в стоит , мы помечаем как . Получается, что мы можем добраться из в с общей стоимостью . При этом указывает, что мы добрались до через вершину .

Шаг 3. Еще мы можем добраться до вершины с общей стоимостью , пройдя через . Вершину уже пометили, но наш маршрут через дешевле, поэтому мы заменим метку на на . Если бы путь к через был дороже, мы бы не меняли метку на . Также мы игнорируем ребро от обратно к , так как было помечено как искомое. И теперь, когда мы закончили с , мы помечаем его как искомый.

Шаг 4. Продолжаем этот процесс для других вершин графа. Всегда выбирайте ту, которую пометили с наименьшей суммарной стоимостью. Она будет помеченной, но не отмеченной как посещенная.

Следующей вершиной для посещения будет , так как ее общая стоимость на данный момент равна , что дешевле, чем у любой другой помеченной вершины. После еще нескольких шагов мы приходим к тому, что — самая дешевая помеченная вершина. Это наша точка остановки.

Как только вершина нашей цели имеет самую дешевую метку, никакой другой маршрут к этой цели не может быть лучше, чем тот, который мы имеем. Поэтому мы останавливаемся на этой точке, и необязательно исследовать остальные пути.

Затем мы используем эти метки, чтобы проследить обратный путь. Например, в конце вершину пометили меткой , поэтому мы прослеживаем путь назад от к . Вершина пометили меткой , поэтому мы прослеживаем путь назад к . Далее — к и к , что дает нам путь с общей длиной как кратчайший путь.

Мы разобрали, что такое алгоритм Дейкстры, и как с его помощью находить кратчайшие пути. Еще он позволяет постоянно улучшать стоимость по мере нахождения лучших путей. Такой алгоритм часто используется в приложениях для маршрутизации сетевых пакетов.