Создание абстракции — JS: Абстракция с помощью данных

Декартова система координат — не единственный способ графического описания. Другой способ — полярная система координат.

Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости однозначно определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой декартовой, или прямоугольной, системе координат, такие отношения можно установить только путём применения тригонометрических уравнений. (c) Wikipedia

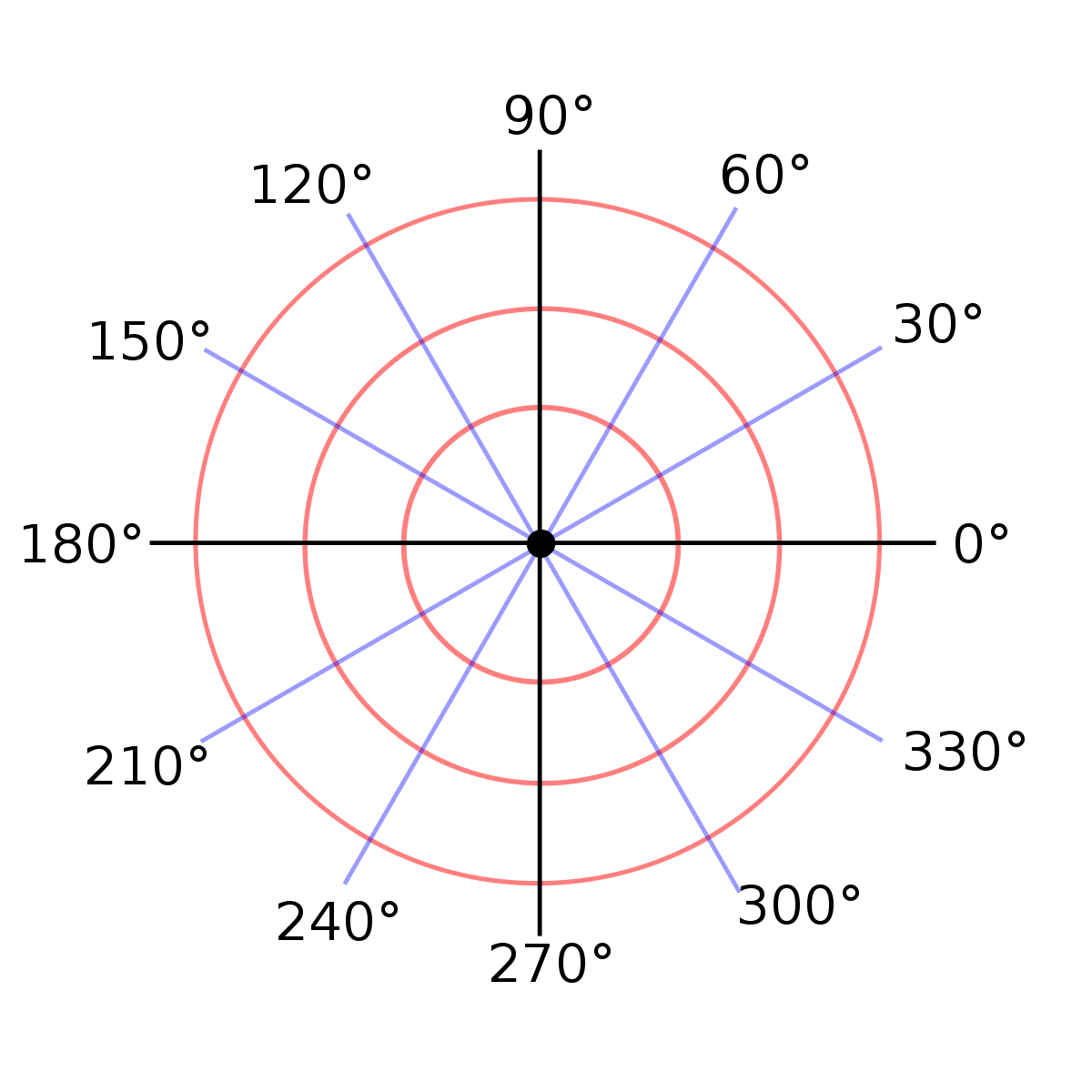
Вообразите себе ситуацию. Вы разрабатываете графический редактор (Photoshop!), и ваша библиотека для работы с графическими примитивами построена на базе декартовой системы координат. В какой-то момент вы понимаете, что переход на полярную систему поможет сделать систему проще и быстрее. Какую цену придётся заплатить за такое изменение? Вам придётся переписать практически весь код.

const point = { x: 2, y: 3 };
const symmetricalPoint = { x: -point.x, y: point.y };

Связано это с тем, что ваша библиотека не скрывает внутреннюю структуру. Любой код, использующий точки или отрезки, знает о том, как они устроены внутри. Это относится как к коду создающему новые примитивы, так и к коду, который извлекает из них составные части. Изменить ситуацию и спрятать реализацию достаточно просто, используя функции:

const point = makePoint(3, 4);
const symmetricalPoint = makePoint(-getX(point), getY(point));

В примере мы видим три функции makePoint(), getX() и getY(). Функция makePoint() называется конструктором, потому что она создает новый примитив, функции getX() и getY() — селекторами (selector), от слова "select", что в переводе означает "извлекать" или "выбирать". Такое небольшое изменение ведёт к далеко идущим последствиям. Главное, что в прикладном коде (том, который использует библиотеку) отсутствует работа со структурой напрямую.

// То есть мы работаем не так
const point = [1, 4]; // мы знаем, что это массив
console.log(point[1]); // прямое обращение к массиву

// А так
const point = makePoint(3, 4); // мы не знаем как устроена точка
console.log(getY(point)); // мы получаем доступ к частям только через селекторы

Глядя на код, даже нельзя сказать, что из себя представляет точка "изнутри", какими конструкциями языка представлена (для этого можно воспользоваться отладочной печатью). Так мы построили абстракцию данных. Суть этой абстракции заключается в том, что мы скрываем внутреннюю реализацию. Можно сказать, что создание абстракции с помощью данных приводит к сокрытию этих данных от внешнего кода.

А вот один из способов реализовать абстракцию для работы с точкой:

const makePoint = (x, y) => ({ x, y });

const getX = (point) => point.x;
const getY = (point) => point.y;

Теперь мы можем менять реализацию без необходимости переписывать весь код (однако, переписывание отдельных частей всё же может понадобиться). Несмотря на то, что мы используем функцию makePoint(), которая создает точку на основе декартовой системы координат (принимает на вход координаты x и y), внутри она вполне может представляться в полярной системе координат. Другими словами, во время конструирования происходит трансляция из одного формата в другой:

const makePoint = (x, y) => {
  // конвертация
  return {
    angle: Math.atan2(y, x),
    radius: Math.sqrt(x ** 2 + y ** 2)
  };
};

Начав однажды работать через абстракцию данных, назад пути нет. Придерживайтесь всегда тех функций, которые вы создали сами. Либо тех, которые вам предоставляет используемая библиотека.

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты

Об обучении на Хекслете

• Статья «Как учиться и справляться с негативными мыслями»
• Статья «Ловушки обучения»
• Статья «Сложные простые задачи по программированию»
• Вебинар «Как самостоятельно учиться»