Операции над множествами — Python: Cловари и множества

• Проверка на равенство
• Объединение множеств
• Пересечение множеств
• Разность множеств
• Симметрическая разность
• Подмножества и надмножества

Если при изучении множеств остановиться на создании и модифицировании, может показаться, что множества не сильно-то и отличаются от списков. Кажется, что они просто позволяют быстрее проверить вхождение элемента, но при этом не поддерживают механизм срезов.

На самом деле, есть более важные аспекты, которые мы и изучим в этом уроке.

Проверка на равенство

Сопоставление множеств — это довольно мощный инструмент. Давайте проверим два множества на равенство:

set([1, 2, 3, 2, 1]) == {3, 1, 2}  # True

Можно подумать, что два множества равны, если каждый отдельный элемент одного множества содержится и во втором. Эта догадка близка к истине, но вспомним, что коллекции в Python хранят только ссылки на объекты. Множества равны, если ссылаются на одни и те же объекты. Одинаковые ссылки равны, но при этом могут быть равны и разные объекты.

Дело в том, что в Python есть специальный протокол проверки на равенство. Большинство встроенных типов данных поддерживает этот протокол. Мы можем проверять на равенство числа, строки, булевы значения. А еще можем приравнивать кортежи, списки, словари.

Здесь Python поступает очень разумно. Если вы приравняете две коллекции одного типа, то эти коллекции будут считаться равными, если их элементы попарно равны с точки зрения протокола. Посмотрите:

[1, 2, ["foo", "bar"]] == [1, 2, ["foo"] + ["bar"]]  # True
(1, True, []) == (1, True, [])  # True
{"a": 1, "b": 2} == {"b": 2, "a": 1}  # True

Словари равны, если порядок ключей разный — лишь бы были равны значения по соответствующим ключам и сами наборы ключей были одинаковыми.

Вот и множества равны, если содержат одинаковые наборы равных попарно элементов.

Объединение множеств

По аналогии с множествами в математике, множества в Python поддерживают операцию объединения (union). Эта операция не объединяет множества, а возвращает новый объект.

Этот объект — это такое множество, которое содержит все элементы, содержащиеся хотя бы в одном из оригинальных множеств. По смыслу объединение похоже на операцию "ИЛИ" из булевой логики: элемент будет присутствовать в объединении, если он присутствует в первом исходном множестве ИЛИ во втором. Так это выглядит на схеме:

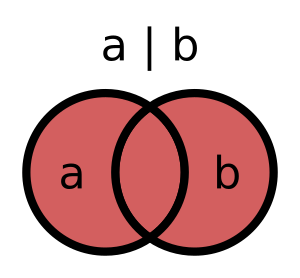
Для объединения множеств в Python используется оператор |:

visited_by_masha = {'Paris', 'London'}
visited_by_kolya = {'Moscow', 'Paris'}
visited_by_kolya | visited_by_masha  # {'London', 'Moscow', 'Paris'}

Пересечение множеств

Еще есть «операция И» — пересечение множеств (intersection). В пересечение входят элементы, присутствующие в первом из оригинальных множеств И во втором:

В Python оператор пересечения — &:

visited_by_masha = {'Paris', 'London'}
visited_by_kolya = {'Moscow', 'Paris'}
visited_by_kolya & visited_by_masha  # {'Paris'}

Разность множеств

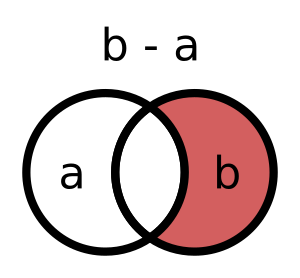
Разность множеств (difference) — такое множество, элементы которого содержатся в первом оригинальном множестве, но не содержатся во втором. Разность представлена оператором -, потому что по смыслу оператор похож на вычитание из арифметики:

visited_by_masha = {'Paris', 'London'}
visited_by_kolya = {'Moscow', 'Paris'}
visited_by_masha - visited_by_kolya  # {'London'}
visited_by_kolya - visited_by_masha  # {'Moscow'}

Так разность можно обозначить на схеме:

Симметрическая разность

Симметрическая разность (symmetric difference) — множество, в которое входят элементы, присутствующие ЛИБО в первом, ЛИБО во втором оригинальном множестве:

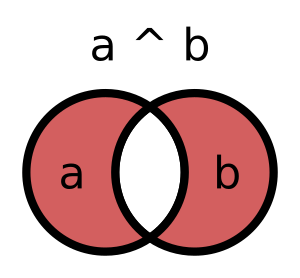
По смыслу операция похожа на исключающее ИЛИ (xor), поэтому и представлена оператором ^:

visited_by_masha = {'Paris', 'London'}
visited_by_kolya = {'Moscow', 'Paris'}
visited_by_kolya ^ visited_by_masha  # {'London', 'Moscow'}

Подмножества и надмножества

Одно множество является подмножеством другого (subset), если все элементы первого входят во второе, но второе может содержать еще и другие элементы. Второе в этом случае является надмножеством для первого (superset):

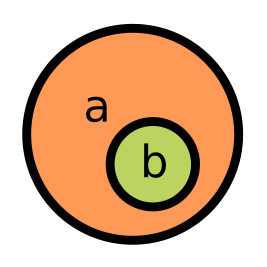
При этом равные множества являются друг для друга одновременно и подмножествами и надмножествами.

В Python соотношение множеств можно проверить с помощью методов issubset и issuperset:

a = {1, 2, 3, 4}
b = {3, 4}
b.issubset(a)  # True
a.issuperset(b)  # True

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты