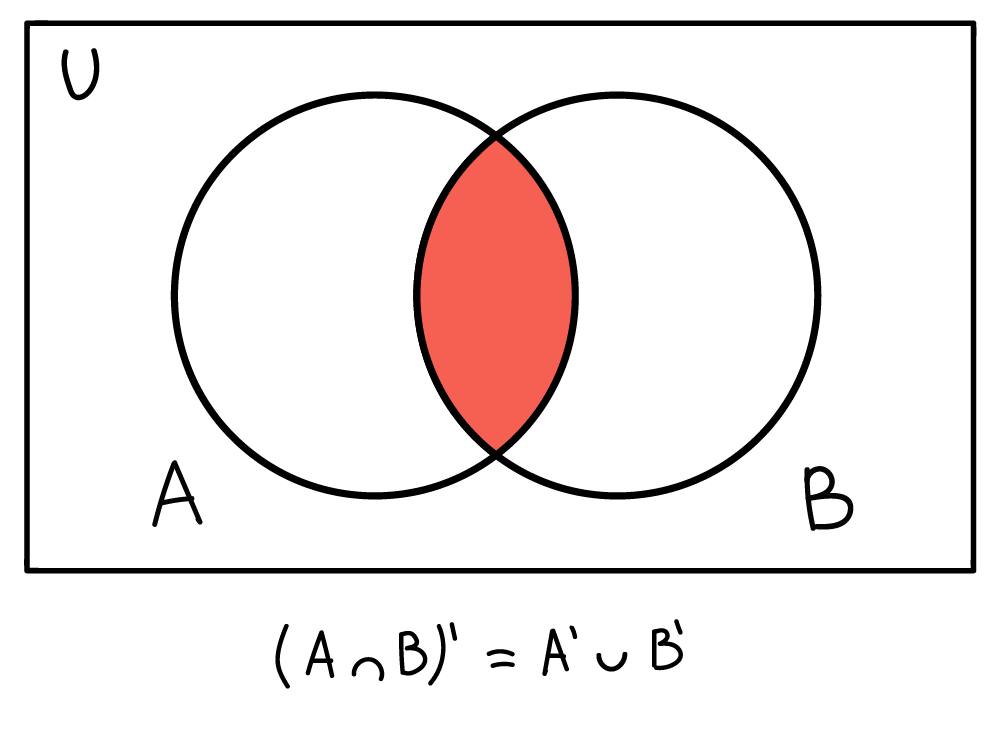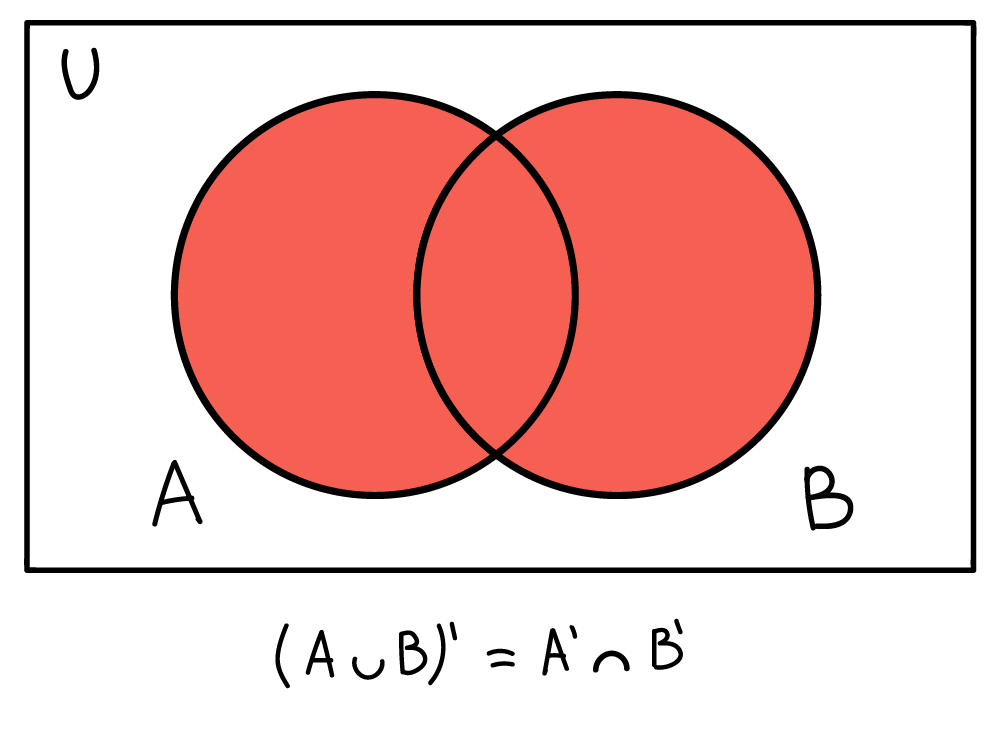- Что такое законы де Моргана?
- Как работают законы де Моргана
- Формула закона де Моргана
- Применение законов де Моргана
Законы де Моргана описывают, как математические утверждения и понятия связаны через их противоположности. В теории множеств законы де Моргана связывают пересечение и объединение множеств через их дополнения.
Если мы хотим упростить операции с множествами, то мы используем законы де Моргана. В этом уроке мы познакомимся с утверждениями законов де Моргана, их применением и примерами.
Что такое законы де Моргана?
Закон де Моргана описывает взаимосвязь между тремя фундаментальными операциями над множествами:
-
Дополнением множеств
-
Объединением множеств
-
Пересечением множеств
В зависимости от взаимосвязи между объединением и пересечением множеств, существует два типа закона де Моргана. Буквально их можно представить так:
-
Не ( и ) — это то же самое, что Не или Не
-
Не ( или ) — это то же самое, что не и не
Для множеств закон де Моргана — это просто наблюдения о связи между множествами и их дополнениями. Простой способ визуализации этих правил — диаграммы Венна.
Переходим к первому закону.
Закон пересечения де Моргана
На диаграмме два множества: и . Мы объединяем их дополнения: на диаграмме это объединение охватывает все пространство, кроме пересечения двух множеств.
Напомним, что дополнение обозначается значком .
Так закон де Моргана для дополнения пересечения двух множеств можно обозначить на схеме:
Дополнение пересечения множеств и — это все пространство на диаграмме, кроме пересечения и .
Оно равно объединению и :
Перейдем к второму закону.
Закон объединения де Моргана
Теперь мы объединяем не дополнения, а сами множества и и смотрим на пересечение их дополнений.
На диаграмме Венна это пересечение охватывает все пространство, кроме объединения двух множеств. Как в первом случае, только наоборот. Отсюда следует закон де Моргана для дополнения объединения двух множеств:
Как и в предыдущем случае, этот закон можно описать такой формулой и показать на диаграмме:
Как работают законы де Моргана
Рассмотрим закон де Моргана на простом примере. Возьмем такое условие задачи:
В ходе недавнего опроса студентов спрашивали, планируют ли они пойти на баскетбольный или футбольный матч.
Всего было опрошено
человек.
учащихся заявили, что они пропустят хотя бы одну из игр. В это число входят и студенты, которые планируют пропустить обе игры.
Сколько студентов планируют посетить обе игры?
Применим закон объединения де Моргана:
студентов пропустят хотя бы одну из игр — это можно интерпретировать как «
студентов пропустят баскетбольную игру или пропустят футбольную игру».
По закону де Моргана, это множество из
студентов является дополнением множества студентов, которые посетят обе игры.
Таким образом, вычислим количество студентов, которые посетят обе игры:
Другой пример:
Найдем, сколько целых чисел от до включительно не являются ни кратными , ни кратными .
Применим закон де Моргана:
По условию:
-
— множество целых чисел от до , которые кратны
-
— множество целых чисел от до , которые кратны
Вопрос состоит в том, чтобы найти .
По законам де Моргана нам надо найти :
-
целых чисел от до , которые делятся на . Это наше множество
-
целых чисел от до , которые делятся на . Это наше множество
-
целых чисел от до , которые кратны и , и
Теперь мы можем найти количество целых чисел от
до
, которые кратны
или
:
Следовательно, количество целых чисел от до , которые не кратны ни ни :
Формула закона де Моргана
Закрепим, что законы де Моргана используется в теории множеств и в булевой алгебре.
Используя эти законы, можно установить связь между объединением и пересечением через дополнение.
Ниже мы разберем различные формы формул в теории множеств:
Также различные формы формул есть в булевой алгебре:
Применение законов де Моргана
Законы де Моргана используются как в элементарной, так и в булевой алгебре. Они помогают сократить сложные выражения, и поэтому широко используются в большинстве инженерных отраслей для создания аппаратуры и упрощения операций.
Рассмотрим такие примеры:
-
Применение закона де Моргана можно увидеть в электронной технике для разработки логических вентилей. С помощью этого закона уравнения могут быть построены с использованием только (И отрицание) или (ИЛИ отрицание). Это приводит к удешевлению аппаратуры
-
Законы де Моргана используются в программировании. Они помогают упростить логические выражения, записанные в коде — тем самым уменьшают количество строк и помогают оптимизировать код. Кроме того, эти законы значительно упрощают и ускоряют проверку некоторых кодов, например на SAS
Самостоятельная работа
Задача №1:
Докажите первый закон де Моргана при таком условии:
Нажмите, чтобы увидеть ответ
Согласно второму закону де Моргана,
.
Таким образом:
*
*
*
*
*
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
