Логотип Хекслета

Теория множеств

Теория: Разность множеств

set-theory-difference-1

В рамках школьной математики все мы научились выполнять сложение, вычитание, умножение и деление чисел. Мы можем применить каждую из этих операций к паре чисел, чтобы получить другое число. Например, при вычитании пары чисел 10 и 7 мы получаем число 3, то есть разность между 10 и 7 равна 3.

Аналогично, есть определенные операции, которые мы можем выполнить над двумя множествами, в результате чего получается другое множество. В этом уроке мы подробно изучим одну из операций над множествами, называемую разностью множеств, ее определение, формулы и примеры.

Разница двух множеств

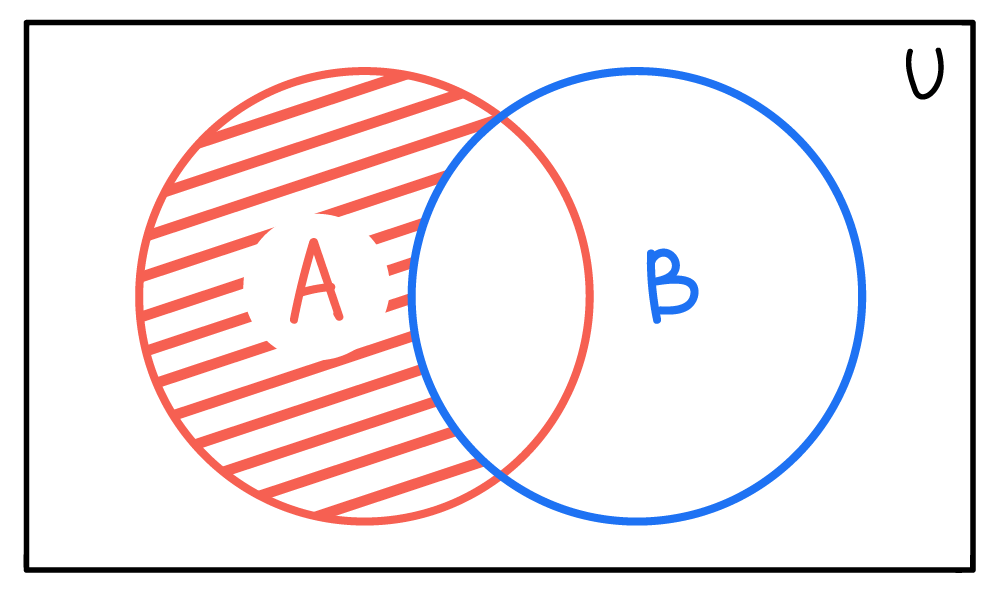
Разность множеств A и B в таком порядке — это множество элементов, которые принадлежат A, но не принадлежат B:

Обозначаем как: A - B, читаем как: «A минус B»

Представление A-B с помощью диаграммы Венна приведено ниже:

set-theory-difference-2

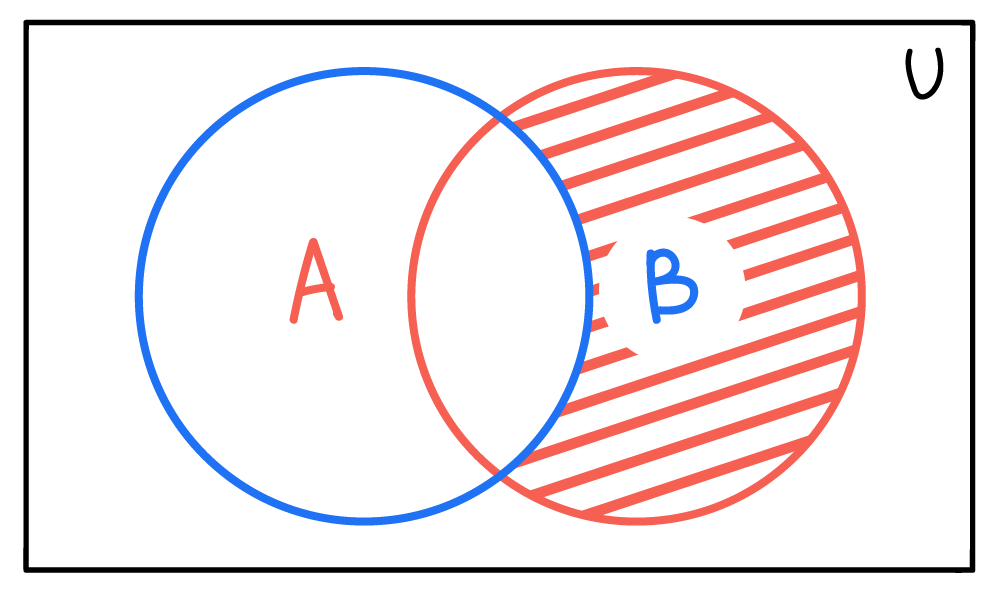
Также мы можем найти B - A. Разность множеств B и A в таком порядке — это множество элементов, которые принадлежат B, но не принадлежат A:

Обозначаем как: B - A, Читаем как: «B минус A»

Диаграмма Венна для B - A будет выглядеть так:

set-theory-difference-3 Также обратите внимание, что A - B не равно B - A, то есть:

A - B != B - A

Симметрическая разность между двумя множествами

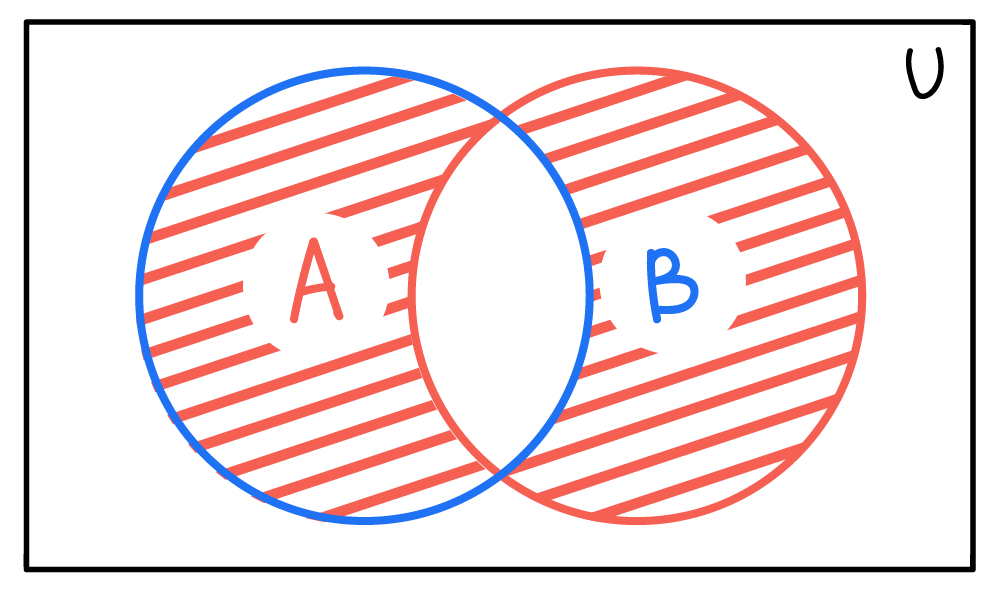
Симметрическая разность множеств содержит элементы, которые находятся либо в множестве A, либо в множестве B, но не в обоих. Она обозначается A ⊝ B и читается как «Симметрическая разность множеств A и B». Так она выглядит на схеме:

set-theory-difference-4

Разность трех множеств

Усложним задачу и попробуем найти разницу между тремя множествами A, B и C.

Предположим, что A, B и C — три непустых множества. Тогда A - B - C представляет собой множество, содержащее элементы A, которые не входят в B и C.

Представление A - B - C в виде диаграммы Венна приведено на следующей диаграмме:

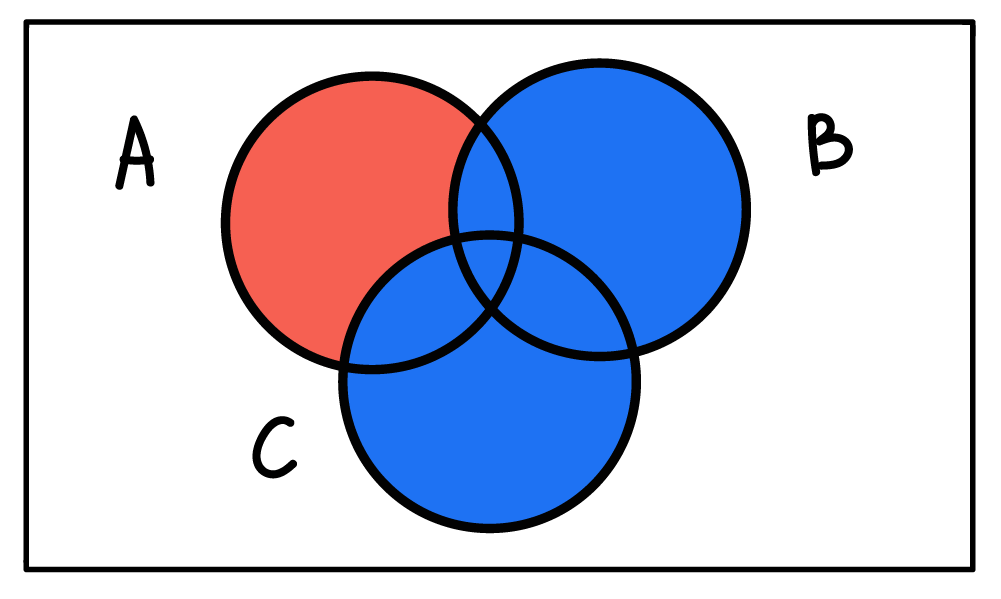
set-theory-difference-5

Правила разности

  • Предположим, что два множества A и B равны. Тогда A - B = A - A = ∅ и B - A = B - B = ∅.
  • Разностью множества и пустого множества является само множество, то есть A - ∅ = A.
  • Разностью пустого и непустого множества является пустое множество, то есть ∅ - A = ∅.
  • Разность множества A от универсального множества U равна пустому множеству, то есть A - U = ∅.
  • Если A и B — непересекающиеся множества (не имеют общих элементов), то A - B = A и B - A = B.

Рекомендуемые программы