- Что такое распределительный закон
- Распределительный закон с переменными
- Распределительный закон при делении
- Распределительный закон с множествами
- Выводы
В математике есть ряд законов и свойств, которые помогают упростить вычисления. С их помощью можно превращать запутанные сложные формулы в простые.
В этом уроке вы познакомитесь с одним из таких законов — он называется распределительным. Это одно из наиболее часто используемых правил в математике. Мы разберем его формулу и рассмотрим решенные примеры, чтобы в дальнейшем вы могли упрощать свои вычисления.
Что такое распределительный закон
Распределительный закон — это алгебраическое свойство, которое используется для умножения нескольких значений в скобках на одно общее значение вне скобок. Само название этого закона означает, что операция подразумевает распределение чего-либо.
По этому закону операцию над числами в скобках можно распределить на каждое отдельное число в этих скобках. Другими словами, можно действовать двумя способами:
- Сначала сложить члены в скобках, а потом умножить их на число вне скобок
- Сначала умножить каждый отдельный член на число вне скобок, а потом сложить результаты
В виде формулы этот закон выглядит еще нагляднее:
A × (B + C) = AB + AC
То же самое работает и с вычитанием:
A × (B - C) = AB - AC
Рассмотрим, как это работает на практике. Возьмем для примера:
2 × (4 + 3)
Вычислить ответ можно двумя способами:
- По обычному порядку действий: сложить 4+3=7 и умножить 7×2=14
- С распределением: умножить 4×2=8 и 3×2=6, а потом сложить 8+6=14
Также в разных источниках вы можете встретить название «дистрибутивный закон» или «распределительное свойство» — эти термины относятся к этому же понятию.
Распределительный закон с переменными
Распределительный закон работает и с переменными. Рассмотрим такой пример:
6 × (2 + 4x)
Два значения внутри скобок — это число и переменная, умноженная на число. Их нельзя сложить друг с другом, поэтому упростить эти значения дальше невозможно. Но мы можем применить распределительный закон к переменной:
6 × 2+6 × 4x
Скобок больше не существует. Каждый член умножается на 6, а потом результаты складываются:
12 + 24x
Выше мы рассмотрели примеры, где распределительный закон упрощает умножение. Обратите внимание, что в этих примерах мы сталкивались только с двумя значениями в скобках. На практике те же принципы применимы и с любым количеством значений и не только к умножению, но и к делению.
Распределительный закон при делении
Мы можем делить большие числа с помощью распределительного закона, разбивая их на меньшие числа.
Для примера разделим 84 ÷ 6. Чтобы упростить эту операцию, можно разбить 84 на более удобные значения:
- 84=60+24
- 84÷6=(60+24)÷6
Теперь распределяем деление на каждое значение в скобках:
- (60 + 24) ÷ 6=(60 ÷ 6) + (24 ÷ 6)
- (60 ÷ 6) + (24 ÷ 6)= 10 + 4
- 10+4= 14
Распределительный закон с множествами
Все те же правила работают и в выражениях с множествами. В этом случае распределительный закон выглядит так:
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C )
То же самое можно обозначить такой формулой:
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C )
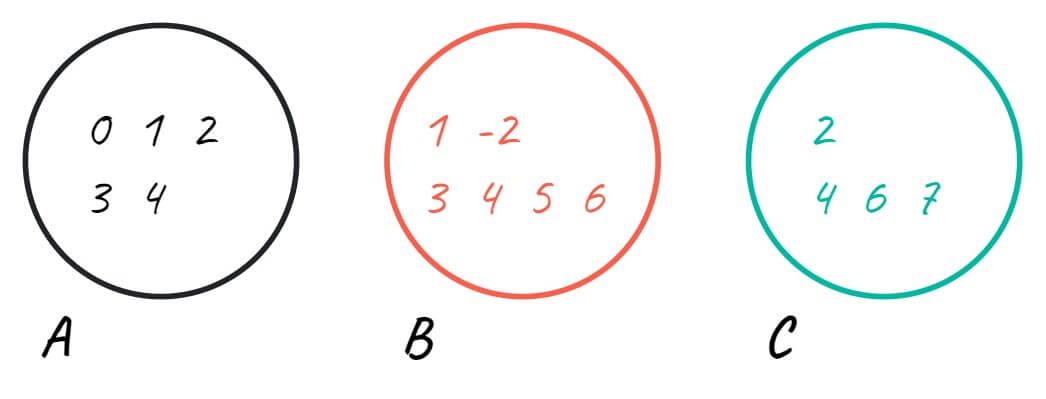
Разберем на примере с диаграммами Венна. Представим, что нам даны три множества:
- A = {0, 1, 2, 3, 4}
- B = {1, -2, 3, 4, 5, 6}
- C = {2, 4, 6, 7}
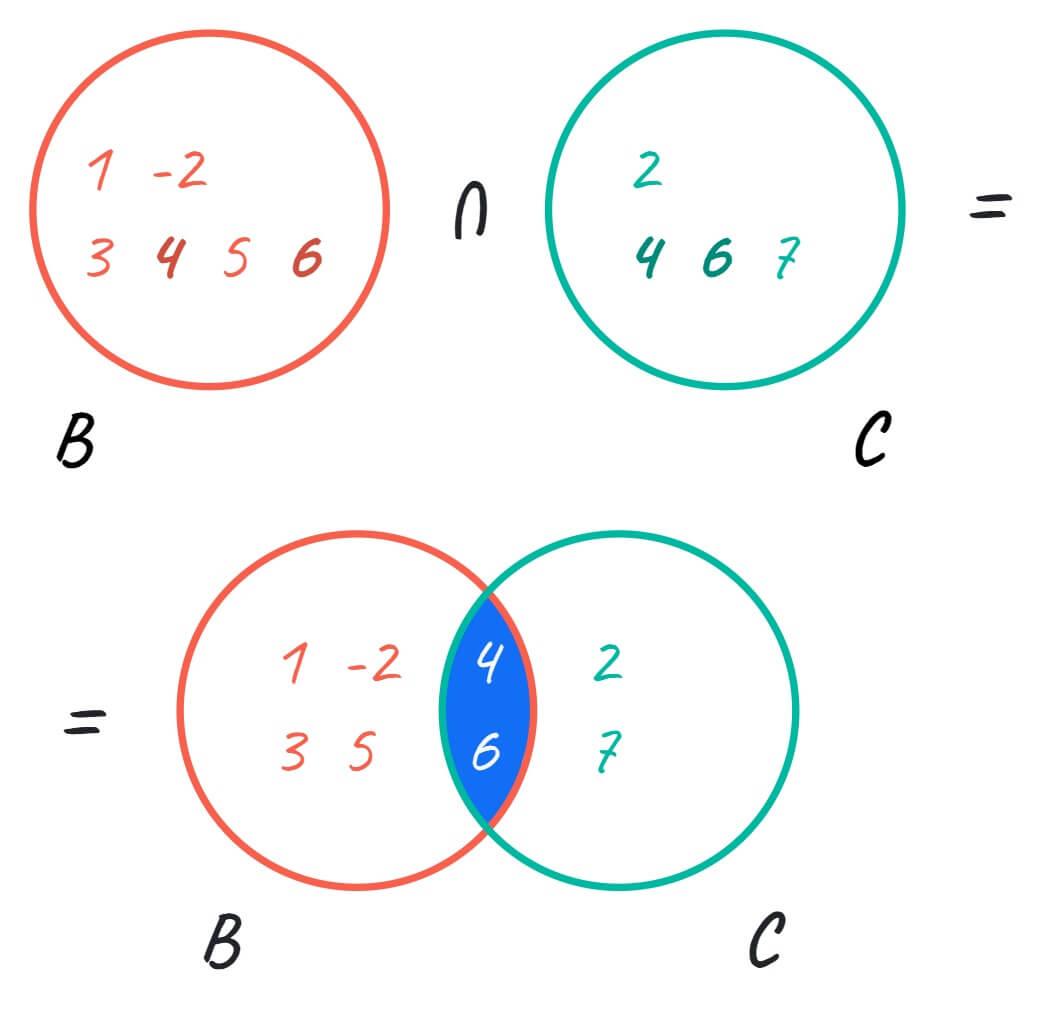
Шаг 1. Сначала найдем общие элементы в B и C:
- B ∩ C = {1, -2, 3, 4, 5, 6} ∩ {2, 4, 6, 7}
- B ∩ C = {4, 6}
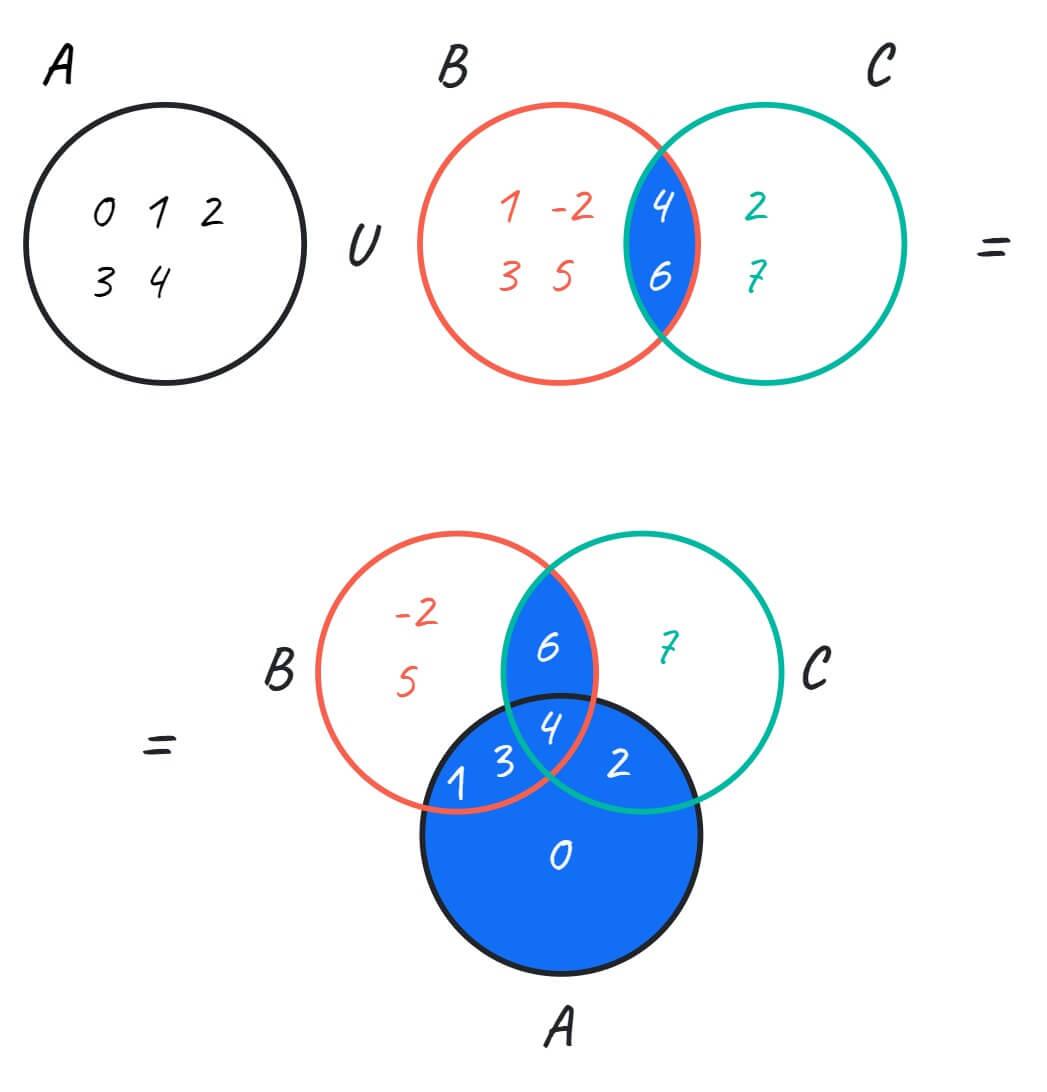
Теперь объединим эти элементы с множеством $A$:
- A ∪ (B ∩ C) = {0, 1, 2, 3, 4} ∪ {4, 6}
- A ∪ (B ∩ C) = {0, 1, 2, 3, 4, 6} — с этим объединением мы и будем сравнивать
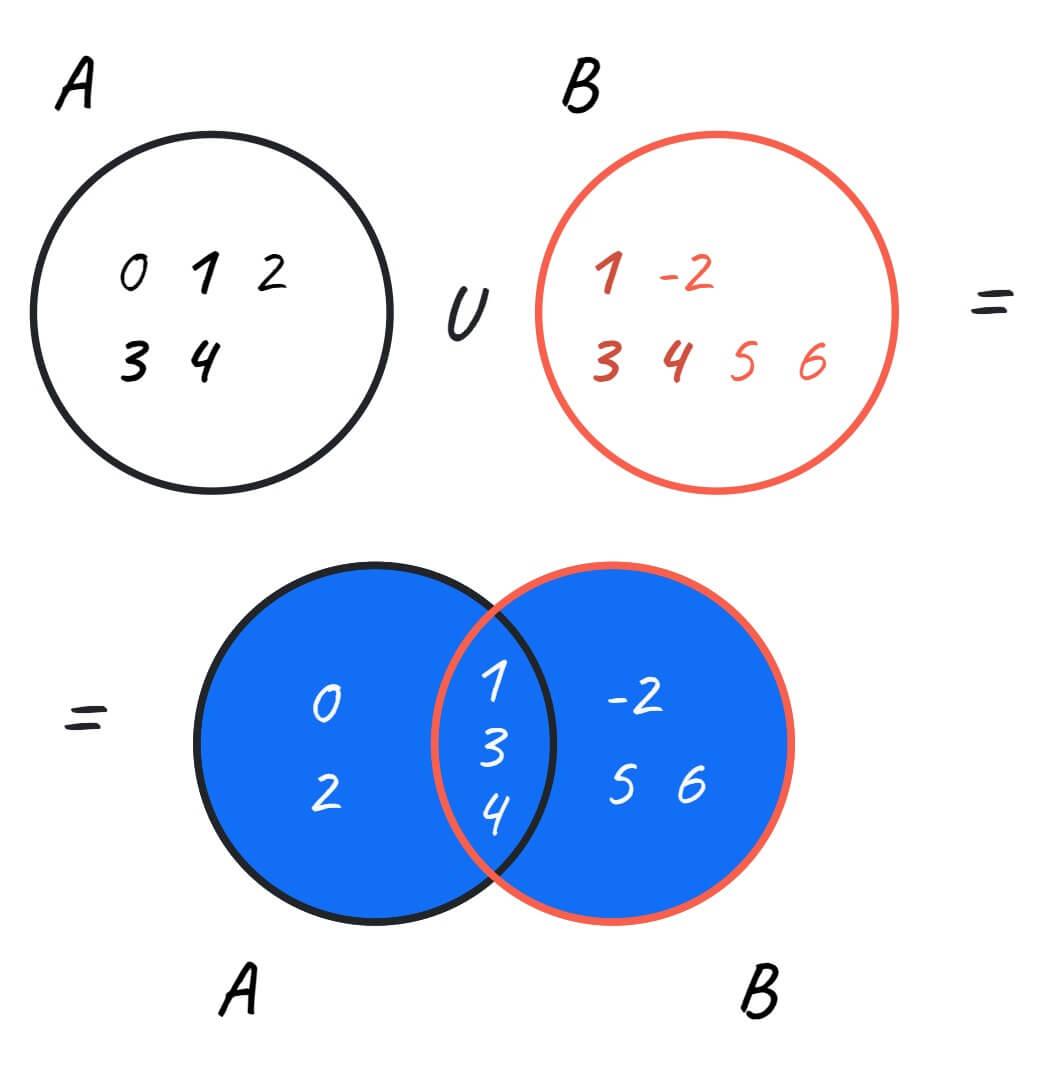
Шаг 2. Объединяем множество $A$ по отдельности. Начнем с $B$:
A ∪ B = {0, 1, 2, 3, 4} ∪ {1, -2, 3, 4, 5, 6} = {-2, 0, 1, 2, 3, 4, 5, 6}
А затем объединим с C:
A ∪ C = {0, 1, 2, 3, 4} ∪ {2, 4, 6, 7} = {0, 1, 2, 3, 4, 6, 7}
Пересечем полученые результаты, то есть найдем совпадающие элементы в них:
* (A ∪ B) ∩ (A ∪ C) = {-2, 0, 1, 2, 3, 4, 5, 6} ∩ {0, 1, 2, 3, 4, 6, 7}
* (A ∪ B) ∩ (A ∪ C) = {0, 1, 2, 3, 4, 6}
Теперь сравним результаты шага 1 и 2:
```text
{0, 1, 2, 3, 4, 6} = {0, 1, 2, 3, 4, 6}
Значит, A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C). Именно это мы и хотели выяснить.
Выводы
В этом уроке мы изучили распределительный закон — одно из наиболее часто используемых правил в математике. С его помощью можно превращать запутанные сложные формулы в простые. Мы можем распределять:
- Умножение по сумме нескольких значений в скобках a(b + c) = ab + ac
- Умножение по разности нескольких значений в скобках a(b - c)=ab - ac
- Деление по сумме нескольких значений в скобках (b+c) ÷ a=(b ÷ a)+(c ÷ a)
- Деление по разности нескольких значений в скобках (b - c)÷a=(b ÷ a)-(c ÷ a)
Те же правила применимы при нескольких значениях в скобках, а также в операциях с множествами. Эти правила помогут вам упрощать выражения в арифметике, алгебре и теории множеств — вы сможете быстрее вычислять и проще приходить к решению задач.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
