Теория множеств

Теория: Нотации

Полный доступ к материалам

Зарегистрируйтесь и получите доступ к этому и десяткам других курсов

set-theory-symbols

Теория множеств — это раздел математики, посвященный изучению коллекций объектов, их свойств и отношений между ними. В этой теме не обойтись без общепринятых условных значений. Без этих знаний вы не сможете понимать математические выражения и дальше продвигаться в изучении дискретной математики.

В этом уроке мы рассмотрим наиболее важные символы в теории множеств — также узнаем, что они значат и как их использовать. Для удобства чтения мы сгруппировали эти символы в таблицы по их функциям.

Константы

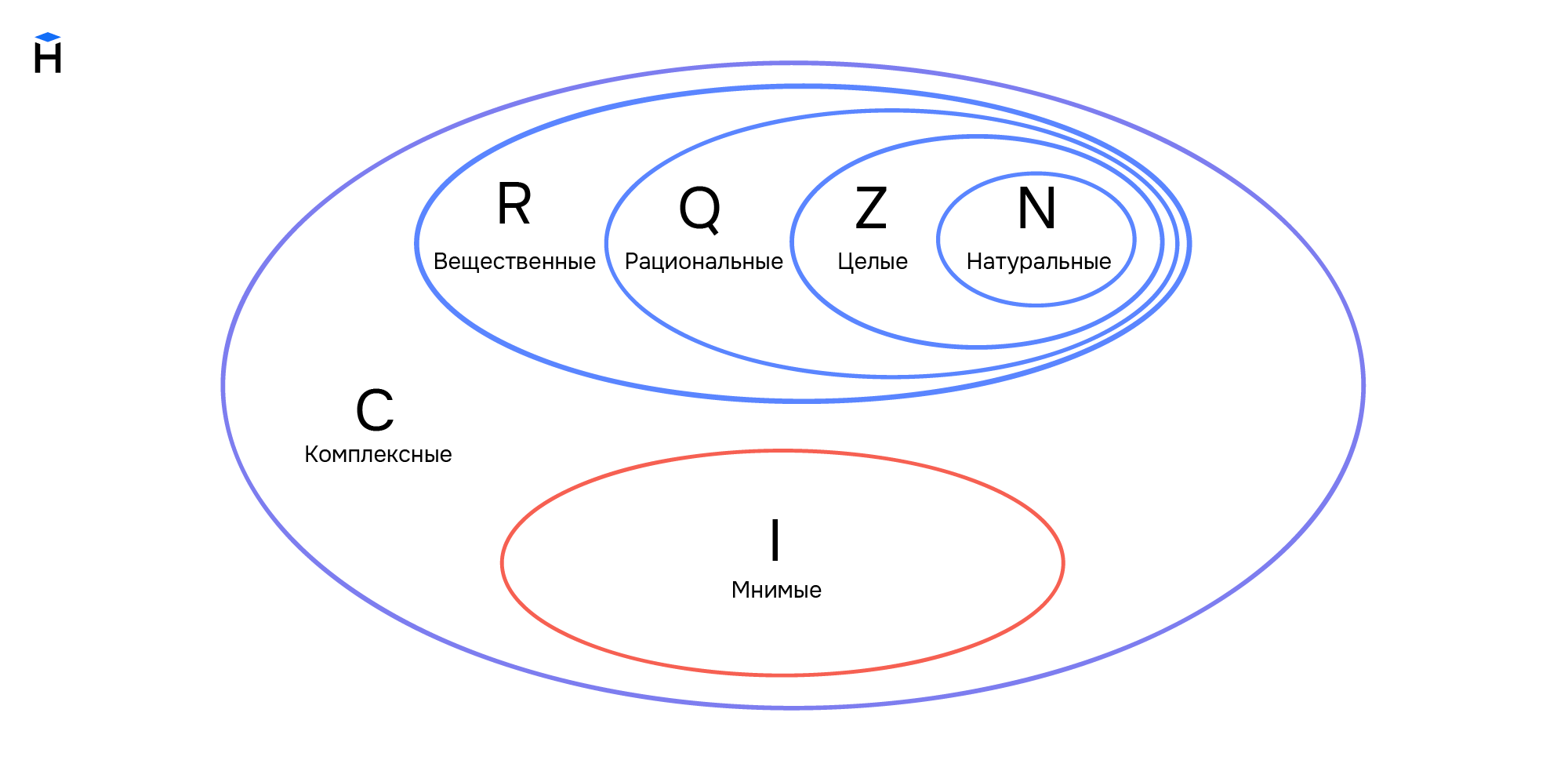
В теории множеств константы — это односимвольные литералы, используемые для обозначения ключевых математических множеств. В таблице ниже мы приводим наиболее заметные из них, а также их значение и примеры:


Ø, ∅, {}	Пустое множество	\|∅\|=0
⊆ {N}	Множество натуральных чисел	1 ∈ {N}
⊆ {Z}	Множество целых чисел	Если m,n ∈ {Z}, тогда m+n, mn ∈ {Z}
⊆ {Q}	Множество рациональных чисел	P ∉ ∈ {Q}
⊆ {I}	Множество иррациональных чисел	Pi ∈ ⊆ {I}
⊆ {R}	Множество действительных чисел	e ∈ {R}
⊆ {C}	Множество комплексных чисел	⊆ {N} ⊆ {Z} ⊆ {Q} ⊆ {R} ⊆ {C}
⊆ {U}	Универсальное множество	Когда U= ⊆ {R}, ⊆ {I}= ⊆ {R} \ ⊆ {Q}

На схеме ниже вы видите, как соотносятся константы между собой:

set-theory-symbols-2

Переменные

Как и в других областях математики, в теории множеств часто используются символы переменных для обозначения различных объектов и величин.

В следующей таблице мы рассмотрим наиболее распространенные константы:


A, B, C	Множества	A ⊆ B ∪ C
a, b, c	Элементы множества	Если a ∈ A и b ∈ B, тогда a , b ∈ A ∪ B
α,β,gamma	Порядковые числа	Если P(β) для всех β<α подразумевает, что P(α) для всех α, тогда P выполняется в общем случае
λ	Предельные ординалы	λ является предельным ординалом, если он не равен ни 0, ни ординалу преемника
κ	Мощность (кардинальные числа)	Для каждого конечного кардинала κ, его преемником является просто κ+1

Разделители

В теории множеств разделители — это символы, используемые для разделения между независимыми математическими сущностями, и часто встречаются в контексте определения множеств.

В следующей таблице мы рассмотрим наиболее распространенные разделители:


{}	Идентификатор для множеств	{37,Pi}
()	Идентификатор для кортежей	(3,7) ∈ {N}
\∣,:	Маркер «Такой, что»	{x^2: ⊆ {Z}}

Реляционные символы

В теории множеств реляционные символы описывают отношения между множествами или отношения между множеством и его элементом.

В следующей таблице мы рассмотрим наиболее распространенные реляционные символы:


x∈Ax∈A	Принадлежит к множеству (Элемент xx входит в множество AA)	2∈N2∈N.
x∉Ax∉A	Непринадлежность к множеству (Элемент xx не входит в множество AA)	Π∉QΠ∉Q
A=BA=B	Эквивалентность множеств (Множества равны)	∅={}∅={}
A⊆BA⊆B	Отношение подмножества (AA является нестрогим подмножеством BB) Символ ⊆⊆ является аналогом ≤, то есть допускается равенство (A=BA=B) множеств	{1,3}⊆{1,3,7}{1,3}⊆{1,3,7} и {1,3,7}⊆{1,3,7}{1,3,7}⊆{1,3,7}
A⊂BA⊂B	Отношение строгого подмножества (AA является строгим подмножеством BB) Символ ⊂⊂ является аналогом <	{1,3}⊂{1,3,7}{1,3}⊂{1,3,7}
AA ⊊ BB	Отношение без подмножества (AA не является подмножеством BB)	Если AA⊊BB, тогда существует такое x∈Ax∈A, что x∉Bx∉B
A⊇BA⊇B	Надмножество (AA является надмножеством BB)	{1,3,7}⊇{7,3}{1,3,7}⊇{7,3}
A⊃BA⊃B	Отношение правильного надмножества (AA является правильным надмножеством BB)	Когда AB⇔A⊂BAB⇔A⊂B
AA ⊋ BB	Отношение без надмножества (AA не является надмножеством BB)	Когда NN⊋R

Каталог

Полный список доступных курсов по разным направлениям

Навигация

Теория