Логистическая регрессия

Логистическая регрессия — это статистический метод, который моделирует вероятность наступления бинарного события. Модель использует исторические данные, набор факторов, влияющих на исход. Результат работы алгоритма — значение от 0 до 1, которое интерпретируется как вероятность принадлежности наблюдения к одному из двух классов. Метод применяется в задачах прогнозирования и классификации, где требуется оценить риск, вероятность или бинарное решение.

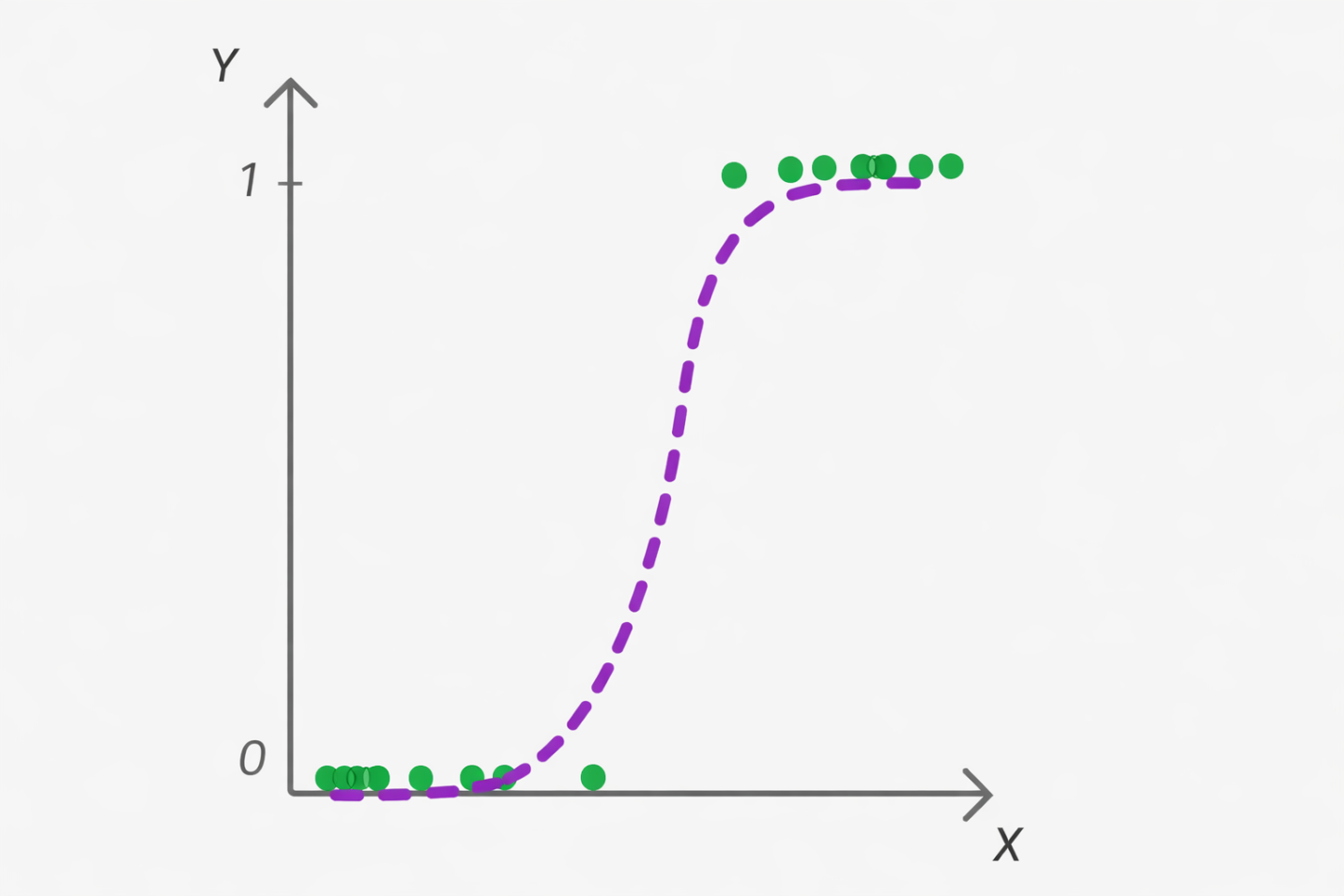
Назначение, общие принципы работы

Логистическая регрессия формирует зависимость между набором независимых переменных и бинарной целевой переменной. Независимые переменные могут быть числовыми, категориальными или бинарными. Модель определяет направление, силу влияния каждого фактора, преобразует линейную комбинацию предикторов в вероятность с помощью логистической функции и выдает итоговое значение вероятности целевого события.

Пример: оценка вероятности оформления кредита. Используются данные о доходе, возрасте, стаже, других атрибутах. На выходе модель формирует вероятность того, что клиент получит одобрение.

Логистическая регрессия включает два ключевых этапа: формирование линейного дискриминанта, преобразование результата в вероятность. Линейная часть задает границу разделения наблюдений, а логистическая функция интерпретирует расстояние до этой границы как вероятность.

Бинарная и множественная регрессия

Простейшая форма модели — бинарная логистическая регрессия. Она применяется, когда целевая переменная принимает два возможных значения. В таких задачах алгоритм разделяет множество объектов на два взаимоисключающих класса.

Существуют также расширенные варианты регрессий:

• Множественная, которая работает с зависимой переменной, имеющей больше двух категорий.

• Порядковая, применяемая при упорядоченных значениях целевой переменной.

• Мультиномиальная, подходящая для задач с неупорядоченными классами.

Все эти разновидности используют единый математический принцип преобразования линейного выражения в вероятности, но отличаются способом обработки целевой переменной и функциями вычисления правдоподобия.

Линейный дискриминант и разделение классов

При визуализации данных наблюдения формируют два облака точек. Между ними ищется разделяющая поверхность. В простых случаях это гиперплоскость, которая делит пространство на две области. Математически такая поверхность описывается линейной функцией.

Пусть координаты наблюдения подставлены в уравнение дискриминанта. Полученное значение обозначается как *t*. Его знак определяет предполагаемый класс объекта:

• t>0 — наблюдение относится к классу «+»;

• t<0 — наблюдение относится к классу «–»;

• t=0 — точка лежит на границе классов.

Чем больше значение |t|, тем выше уверенность в принадлежности к определенной области. Значение t отражает лишь относительное положение точки, но не дает вероятности.

Преобразование t в вероятность

Логистическая регрессия использует экспоненциальное преобразование. Сначала вычисляется отношение шансов:

e^t

Затем оно преобразуется в вероятность:

P+ = e^t / (1 + e^t)

Эта формула ограничивает результат диапазоном от 0 до 1. Если t велико, вероятность стремится к 1; если t мало или отрицательно — к 0. Такое отображение удобно для бинарных решений и позволяет интерпретировать линейную модель в вероятностной форме.

Где используется логистическая регрессия

Метод востребован в аналитике и инженерных задачах. Его применяют там, где требуется интерпретируемая модель и точная оценка вероятности. Основные сферы:

• машинное обучение — классификация, оценка риска, детекция событий;

• нейронные сети — логистическая функция используется в качестве активации для бинарных выходов;

• анализ данных — оценка вероятностей на основе наблюдений;

• финансовая индустрия — кредитный скоринг, риск-модели;

• медицина — прогноз вероятности диагноза или наступления клинических событий;

• маркетинг и бизнес-аналитика — прогноз кликов, покупок, отказов, отклика на предложение.

Метод используют, когда важна прозрачность параметров и контроль качества модели. Коэффициенты логистической регрессии легко интерпретировать, что делает ее удобной в корпоративных системах принятия решений.

Отличие логистической регрессии от линейной

Обе модели используют линейную комбинацию предикторов, однако их цели и свойства различаются. Линейная регрессия моделирует непрерывное значение целевой переменной и формирует прямую линию или гиперплоскость. Логистическая регрессия оперирует вероятностями и использует S-образную сигмоиду.

Основные различия:

• Результат:

• линейная регрессия дает числовое значение;

• логистическая — вероятность.

• Форма функции:

• линейная — прямая;

• логистическая — ограниченная кривая.

• Оптимизация:

• линейная — метод наименьших квадратов;

• логистическая — метод максимального правдоподобия.

Графическая форма делает логистическую регрессию устойчивой к аномальным значениям целевой переменной. Результат всегда остается в допустимом интервале, что важно для вероятностных предсказаний.

Требования к данным

Корректность результатов зависит от нескольких условий. Нарушение предпосылок ведет к смещению коэффициентов и снижению качества модели.

Основные требования:

1. Линейность зависимости между логитом вероятности и предикторами.

2. Отсутствие коллинеарности независимых переменных. Если два признака описывают одно и то же, модель становится нестабильной.

3. Изменчивость предикторов. Если переменная постоянна во всех наблюдениях, ее влияние невозможно оценить.

4. Независимость наблюдений. Значения не должны зависеть друг от друга.

5. Гомоскедастичность. Разброс значений вокруг линии логита должен быть приблизительно одинаковым.

Эти требования делают модель устойчивой и обеспечивают корректную интерпретацию коэффициентов.

Подготовка данных

Перед вычислением модели применяются вспомогательные процедуры. Они улучшают качество предсказаний и устраняют влияние шумов.

Типичные действия:

• фильтрация выбросов;

• удаление дублей;

• проверка предикторов на взаимную зависимость;

• нормализация и кодирование категориальных признаков;

• группировка данных при наличии повторяющихся структур.

Подготовка данных обеспечивает выполнение статистических предпосылок и уменьшает риск переобучения.

Инструменты для вычисления логистической регрессии

Метод реализован во множестве аналитических инструментов:

• Excel — содержит встроенные функции для анализа, построения графиков и работы с большими таблицами;

• Python — стандартные библиотеки (например, scikit-learn) поддерживают обучение и интерпретацию моделей;

• R — специализированный язык для статистики, включающий широкий набор функций для регрессионного анализа;

• Power BI — корпоративная аналитическая платформа, позволяющая автоматизировать вычисления и визуализацию.

Инструменты автоматизируют вычисления, но не устраняют необходимость понимать статистические свойства метода.

Практические аспекты применения

Логистическая регрессия используется в задачах, где важна интерпретация коэффициентов. Каждый коэффициент отражает вклад предиктора в изменение логита вероятности. Знак коэффициента показывает направление влияния, а величина — силу.

Модель легко масштабируется, работает с большим количеством наблюдений и не требует значительных вычислительных ресурсов. Она подходит для систем онлайн-прогнозирования и используется во многих инструментах принятия решений.