- Ссылочная прозрачность
- Устройство списков
- Стоимость операций для списков
- Рекурсивные функции с аккумуляторами
- Хвостовая рекурсия
Ссылочная прозрачность
Эрланг, как и большинство других функциональных языков, поддерживает концепцию ссылочная прозрачность (referential transparency).
Что это такое объясню на примере. Допустим, мы создали некую структуру данных, сохранили ее в некой области памяти, и присвоили как значение некой переменной. При этом в переменной сохраняется ссылка на эту область памяти. Я могу передавать переменную в функцию. При этом значение передается по ссылке, а не копируется. Но функция не может изменить это значение. Так что передача по ссылке безопасна.
Эрланг гарантирует, что выделенная память не модифицируется, и значение, однажды присвоенное переменной, никогда не изменится. По сути в функциональных языках нет переменных, а есть только константы.
Благодаря ссылочной прозрачности:
- устраняется определенный класс ошибок;
- упрощается отладка;
- компилятор имеет больше возможностей для оптимизации кода;
- статический анализатор имеет больше возможностей для проверки корректности кода.
Плата за это -- несколько менее эффективные структуры данных, чем в императивных языках.
Устройство списков
Списки, как и любые другие структуры данных, являются неизменяемыми.
Вот мы создаем список и присваиваем его переменной List:
List = [1, 2, 3, 4].
В памяти у нас появляется вот такая структура:
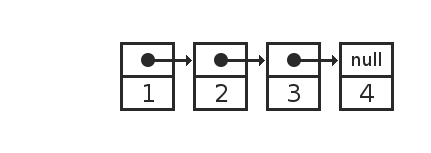
4 элемента списка сохраняются в виде пар ссылка + значение, где ссылка указывает на предыдущий элемент. В последнем элементе ссылка нулевая, никуда не указывает.
Как же нам добавить новый элемент? Этот список мы модифицировать не можем, но можем создать новый список, включающий один новый элемент и все элементы старого списка:
List2 = [0 | List].
Оператор | называется cons, он добавляет новый элемент к голове списка и возвращает новый список.
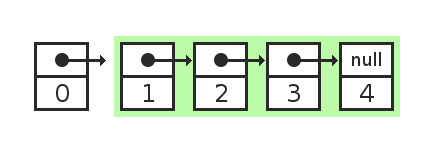
В новом элементе ссылка указывает на первый элемент списка List. В самом списке List ничего не меняется. Область памяти, которую он занимает, модифицировать не нужно.
Итого, у нас теперь есть два списка. Но при этом расход памяти минимальный, ибо большая ее часть используется обоими списками.
Любой список можно представить как последовательность операторов cons:
[0 | [1 | [2 | [3 | [4 | []]]]]]
Или схематически:
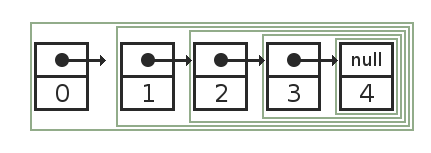
Оператор cons используется и для добавления элемента в начало списка, и для разделения списка на начальный элемент (голова) и все остальные элементы (хвост).
[Head | Tail] = List.
А что было бы, если бы мы использовали двунаправленный связанный список? Он представлен в памяти так:
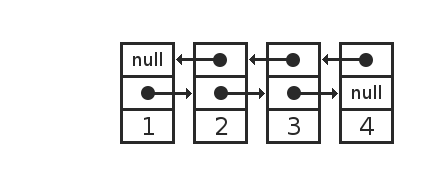
Каждый элемент состоит из значения и двух ссылок. Одна ссылка указывает на предыдущий элемент, другая ссылка на следующий элемент.
И попробуем добавить к такому списку новое значение.
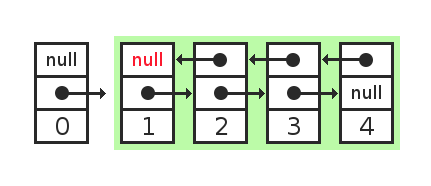
Ссылка в новом элементе указывает на голову списка. Но еще нужно в голове списка поменять ссылку, чтобы она указывала на новый элемент. Поменять ссылку -- это значит, модифицировать память, нарушить ссылочную прозрачность.
Ок, мы можем не модифицировать ссылку в элементе, а скопировать весь элемент:
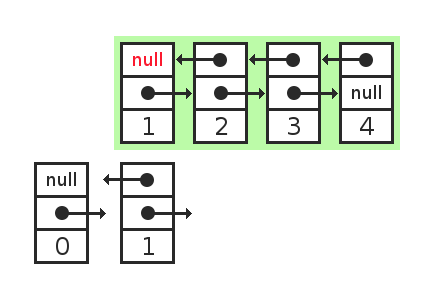
Но теперь нужно менять ссылку в предыдущем элементе. А значит, нужно копировать и его тоже. И таким образом мы скопируем весь список целиком.
Двунаправленные связанные списки делают невозможным использование одного участка памяти несколькими списками. Для каждого придется выделять отдельный участок памяти. А если учесть, что добавление одного элемента, это создание нового списка, то расход памяти будет очень большим.
Стоимость операций для списков
- добавить элемент в начало списка - O(1);
- добавить элемент в конец списка - O(n) и полное копирование памяти;
- определить длину списка - O(n);
- получить N-й элемент - O(n).
Еще рассмотрим суммирование двух списков:
List1 ++ List2.
Стоимость этой операции O(n), где n длина первого списка. Память первого списка копируется, память второго списка используется повторно.
Тут важно, чтобы List1 был коротким, а длина List2 не важна. Часто мы не знаем длинны List1 и поэтому операцию сложения списков считаем дорогой. На одном из последующих уроков мы узнаем, как избегать этой операции с помощью iolist.
Для сравнения, стоимость операций для массивов в императивных языках:
- добавить элемент в начало массива - O(n), ибо все остальные элементы нужно сдвигать;
- добавить элемент в конец массива - O(1), если мы укладываемся в размер массива, O(n) если массив нужно увеличивать;
- определить длину массива - O(1);
- получить/модифицировать N-й элемент - O(1).
Самое главное преимущество массивов над списками -- константное время доступа к любому элементу. Цена за это: потеря ссылочной прозрачности.
В Эрланг есть модуль array, реализующий массивы. Но разработчики его не используют, ибо этот модуль не дает константного времени доступа к любому элементу, и, значит, не имеет никаких преимуществ над списками.
Рекурсивные функции с аккумуляторами
Типичный способ работы со списками -- использование рекурсивных функций и аккумуляторов. Рассмотрим эту тему на конкретных примерах.
Допустим, у нас есть список пользователей:
Users = [{user, 1, "Bob", male},
{user, 2, "Helen", female},
{user, 3, "Bill", male},
{user, 4, "Kate", female}].
И мы хотим отфильтровать пользователей женского пола. То есть, получить новый список, где будут только девушки.
Применим рекурсивную функцию с аккумулятором:
filter_female([], Acc) -> Acc;
filter_female([User | Rest], Acc) ->
case User of
{user, _, _, male} -> filter_female(Rest, Acc);
{user, _, _, female} -> filter_female(Rest, [User | Acc])
end.
Функция получает на вход два аргумента: список пользователей, и список, где будет накапливаться результат выполнения -- аккумулятор. В начале выполнения список пользователей полный, а аккумулятор пустой. На каждом шаге итерации мы будем брать один элемент из первого списка, и, если он нам нужен, то класть его в аккумулятор. В итоге первый список опустошится, а аккумулятор наполнится.
Наша рекурсивная функция имеет два тела (clause). В зависимости от входящих аргументов выполняется либо одно тело, либо другое. Тут действует сопоставление с образцом (pattern matching), который мы будем рассматривать позже. Сейчас мы просто знаем, что первое тело выполняется, когда список пользователей пустой. То есть, это завершение фильтрации. И тут нужно просто отдать накопленный результат.
Второе тело и делает всю работу. Сперва список пользователей с помощью оператора cons делится на голову и хвост (это можно делать прямо в описании аргументов функции). Голова -- это текущий элемент списка, который мы будем анализировать. Хвост -- это остаток списка, который мы передадим дальше, в следующий рекурсивный вызов.
Анализ элемента тут простой: с помощью конструкции case и сопоставления с образцом определяем пол пользователя. Пользователей мужского пола мы игнорируем, а женский пол добавляем в аккумулятор, опять с помощью оператора cons.
case и сопоставление с образцом пока что не изучены, но вы ведь уже прочитали об этом в рекомендованных книгах, правда? Если нет, то самое время прочитать :) Увы, в практических упражнениях приходится немного забегать вперед, ибо без этих конструкций мало чего полезного можно сделать :)
Элементы в аккумуляторе накапливаются в обратном порядке. Если это не важно, то аккумулятор можно вернуть, как есть. Если желательно сохранить оригинальный порядок, то аккумулятор нужно развернуть:
filter_female([], Acc) -> lists:reverse(Acc);
Второй пример. Допустим, из списка пользователей нужно извлечь их идентификаторы и имена. То есть, получить список кортежей вида:
{Id, Name}
Делаем:
get_names([], Acc) -> lists:reverse(Acc);
get_names([User | Rest], Acc) ->
{user, Id, Name, _} = User,
get_names(Rest, [{Id, Name} | Acc]).
Опять два тела у функции. Первое тело отвечает за завершение рекурсии и возврат результата, накопленного в аккумуляторе.
Второе тело обрабатывает каждый элемент списка, извлекает из кортежа {user, Id, Name, Gender} нужные данные Id и Name, и сохраняет их в аккумуляторе.
Хорошая практика -- предлагать как публичный АПИ функцию с одним аргументом. А функцию с аккумулятором скрывать от пользователей модуля. Потому что аккумулятор может быть сложнее, чем просто список, и пользователям модуля незачем об этом знать.
get_names(Users) -> get_names(Users, []).
get_names([], Acc) -> lists:reverse(Acc);
get_names([User | Rest], Acc) ->
{user, Id, Name, _} = User,
get_names(Rest, [{Id, Name} | Acc]).
И вот пример со сложным аккумулятором. Допустим нам нужно разделить пользователей на два списка. В первом те, кому меньше 18 лет, во втором от 18 и старше. Тут, конечно, будет немного другой список пользователей, с указанием возраста:
Users = [{user, 1, "Bob", male, 27},
{user, 2, "Helen", female, 18},
{user, 3, "Bill", male, 15},
{user, 4, "Kate", female, 11}].
Реализация:
partition_users(Users) -> partition_users(Users, {[], []}).
partition_users([], {List1, List2}) -> {lists:reverse(List1), lists:reverse(List2)};
partition_users([User | Rest], {List1, List2}) ->
{user, _, _, _, Age} = User,
if
Age < 18 -> partition_users(Rest, {[User | List1], List2});
true -> partition_users(Rest, {List1, [User | List2]})
end.
На сей раз наш аккумулятор -- это кортеж из двух списков. В первом теле функции, как обычно, возвращаем результат. И тут мы разворачиваем оба списка. Во втором теле функции обрабатываем каждый элемент списка, извлекаем и проверяем возраст. Тех, кто моложе 18 лет, кладем в первый список в аккумуляторе, остальных во второй список.
Хвостовая рекурсия
В эрланг, как и во всех функциональных языках, нет циклов. Их заменяет рекурсия. Надо понимать, что рекурсия -- штука не бесплатная. Каждый рекурсивный вызов требует сохранения на стеке предыдущего состояния функции, чтобы вернуться в него после очередного вызова.
И хотя стек в эрланге легковесный и позволяет делать миллионы рекурсивных вызовов, (а не тысячи, как, в императивных языках), он, все-таки, конечный.
Поэтому в эрланг, как и во многих других функциональных языках, компилятор делает одну полезную штуку, которая называется оптимизация хвостовой рекурсии.
Если рекурсивный вызов является последней строчкой кода в данной функции, и после него больше никаких инструкций нет, то такой вызов называется хвостовым. В этом случае нет необходимости возвращаться по стеку во все вызывающие функции, а можно сразу отдать результат из последнего вызова. И стек не растет, а используется заново каждым новым вызовом, и адрес возврата в нем не меняется.
Это позволяет делать бесконечную рекурсию, которая нужна для бесконечно живущих процессов. А такие процессы нужны серверам :)
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты