JS: Массивы
Теория: Big O
Когда заходит речь про алгоритмы, нельзя не упомянуть понятие «сложность алгоритма» (обозначается как Big O). Оно дает понимание того, насколько эффективен алгоритм.
Как вы помните, алгоритмов сортировок существует много. Все они выполняют одну и ту же задачу, но при этом отличаются друг от друга. В информатике алгоритмы сравниваются друг с другом по их алгоритмической сложности. Эта сложность — количество выполняемых операций алгоритмом для достижения своей цели. Например, разные способы сортировки требуют разного количества "проходов" по массиву перед тем, как массив будет полностью отсортирован. Понятно, что конкретное количество операций зависит от входных данных, например, если массив уже отсортирован, то количество операций будет минимальным (но они все равно будут, потому что алгоритм должен убедиться в том, что массив отсортирован).
Big O как раз придумана для описания алгоритмической сложности. Она призвана показать, как сильно увеличится количество операций при увеличении размера данных.
Вот некоторые примеры того, как записывается сложность: O(1), O(n), O(nlog(n)).
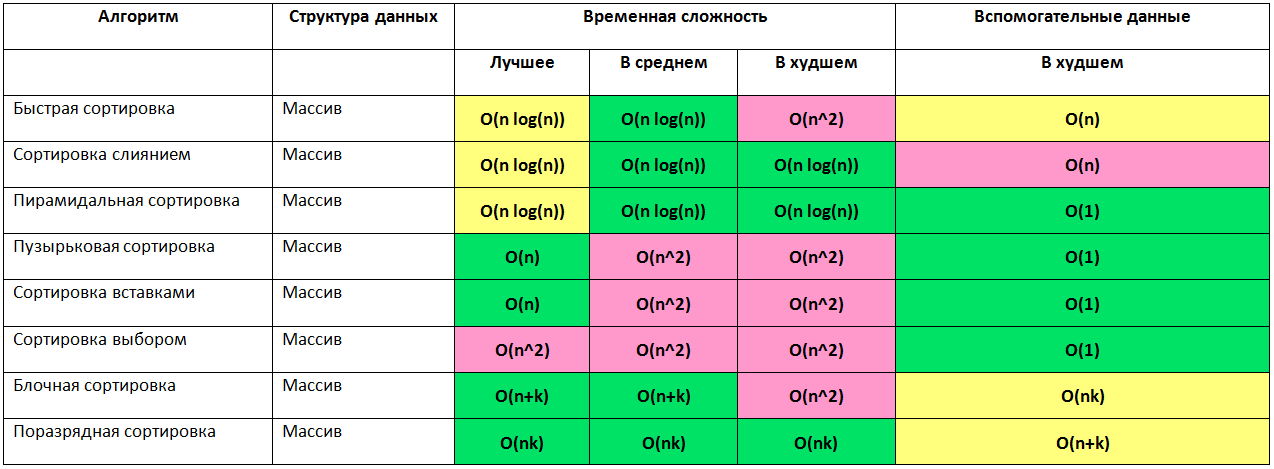
O(1) описывает константную (постоянную) сложность. Такой сложностью обладает операция доступа к элементу массива по индексу. Сложность (в алгоритмическом смысле) доступа к элементу не зависит от размеров массива и является величиной постоянной. А вот функция, которая печатает на экран все элементы переданного массива, используя обычный перебор, имеет сложность O(n) (линейная сложность). То есть количество выполняемых операций, в худшем случае, будет равно количеству элементов массива. Именно это количество символизирует символ n в скобках.
Что такое худший случай? В зависимости от того, в каком состоянии находится начальный массив, количество операций будет разным даже при условии, что массив одного и того же размера. Чтобы проще понять, возьмем в качестве аналогии кубик Рубика. Количество операций (действий) которые нужно проделать для сборки кубика Рубика зависит от того, в каком положении находятся его грани перед сборкой. В некоторых случаях действий понадобится мало, в других много. И вот та ситуация, в которой таких действий понадобится больше всего, и называется худшим случаем. Алгоритмическая сложность всегда оценивается по худшему случаю для выбранного алгоритма.
Еще один пример — вложенные циклы. Вспомните как работает поиск пересечений в неотсортированных массивах. Для каждого элемента из одного массива проверяется каждый элемент другого массива (либо через цикл, либо с помощью метода includes(), чья сложность O(n), ведь в худшем случае он просматривает весь массив). Если принять, что размеры обоих массивов одинаковы и равны n, то получается, что поиск пересечений имеет квадратичную сложность или O(n^2) (n в квадрате).
Существуют как очень эффективные, так и абсолютно неэффективные алгоритмы. Скорость работы подобных алгоритмов падает с катастрофической скоростью даже при небольшом количестве элементов. Нередко более быстрые алгоритмы быстрее не потому, что они лучше. Дело в том, что они потребляют больше памяти или имеют возможность запускаться параллельно (и если это происходит, то работают крайне эффективно). Как и все в инженерной деятельности, эффективность — компромисс. Выигрывая в одном месте, мы проиграем где-то в другом.
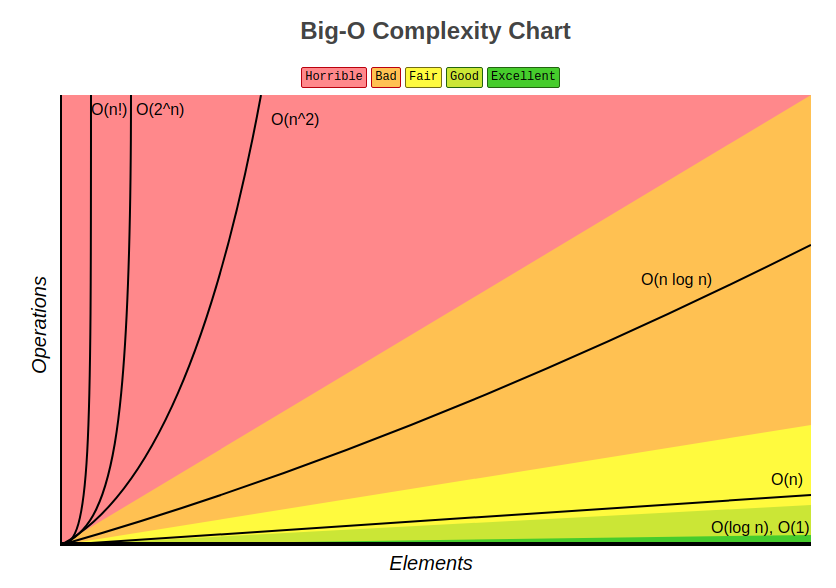
Big O — во многом теоретическая оценка. На практике все может быть по-другому. Реальное время выполнения зависит от множества факторов, среди которых: архитектура процессора, операционная система, язык программирования, доступ к памяти (последовательный или произвольный) и многое другое.
Вопрос эффективности кода довольно опасен. В силу того, что многие начинают учить программирование именно с алгоритмов (особенно в университете), им начинает казаться, что эффективность — это главное. Код должен быть быстрым.
Такое отношение к коду гораздо чаще приводит к проблемам, чем делает его лучше. Важно понимать, что эффективность — враг понимаемости. Такой код всегда сложнее, больше подвержен ошибкам, труднее модифицируется, дольше пишется. А главное, настоящая эффективность редко когда нужна сразу или вообще не нужна. Обычно тормозит не код, а, например, запросы к базе данных или сеть. Но даже если код выполняется медленно, то вполне вероятно, что именно тот участок, который вы пытаетесь оптимизировать, вызывается за все время жизни программы всего лишь один раз и ни на что не влияет, потому что работает с небольшим объемом памяти, а где-то в это время есть другой кусок, который вызывается тысячи раз, и приводит к реальному замедлению.
Программисты тратят огромное количество времени, размышляя и беспокоясь о некритичных местах кода, и пытаются оптимизировать их, что исключительно негативно сказывается на последующей отладке и поддержке. Мы должны вообще забыть об оптимизации в, скажем, 97% случаев. Поспешная оптимизация является корнем всех зол. И, напротив, мы должны уделить все внимание оставшимся 3%. — Дональд Кнут
Перед тем, как пытаться что-то оптимизировать, обязательно прочитайте небольшую онлайн-книжку, которая хорошо объясняет суть всех оптимизаций.
Рекомендуемые программы
Завершено
0 / 22




