Умение работать со средними и медианными значениями помогает сравнивать однородные данные и выяснять, у какой выборки та или иная цифра больше. Оба показателя используются, чтобы одной цифрой охарактеризовать целый набор величин — например, сумму продаж или возраст людей.
Для начала коротко рассмотрим разницу на примере оценки зарплат:
- Среднее значение поможет вычислить среднюю сумму, но эти данные будут искажаться из-за нетипично низких или аномально высоких зарплат некоторых сотрудников
- Медианное значение покажет сумму без искажения, потому что с его помощью мы можем оценить форму распределения данных и выделить на графике отклонения или аномалии
Как видно на примере выше, разница заключается в аномальных значениях — выбросах.
Выбросы
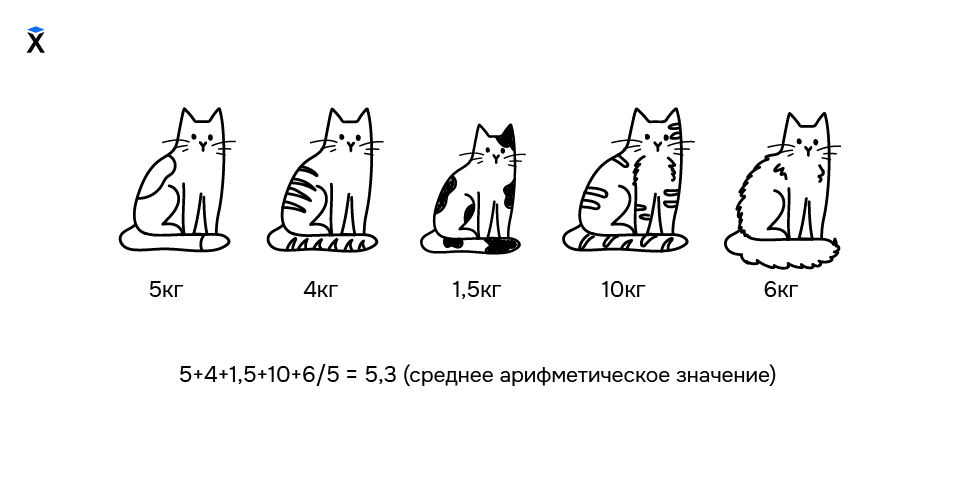
Выбросы — это аномально маленькие или большие значения в наборе данных. Например, мы хотим выяснить типичный вес среди пяти котиков:
- Вася — 5 кг
- Мурка — 4 кг
- Бусинка – 1.5 кг
- Пушок — 10 кг
- Алиса — 6 кг
Выбросами будут вес Бусинки и Пушка — эти значения аномально отличаются от всех остальных.
Как найти самый типичный вес котика? Чтобы оценить набор величин с помощью одной величины, можно использовать разные метрики и статистические показатели:
- Среднее арифметическое
- Медиана
- Мода
- Математическое ожидание
- Дисперсия
- Стандартное отклонение
В этом уроке мы поговорим подробно о среднем арифметическом, медиане и моде.
Среднее арифметическое
Среднее значение — это простой способ вычислить среднее значение в наборе чисел. Нужно просто сложить все числа, а затем разделить полученную сумму на общее количество чисел в наборе.
(3 + 7 + 13) / 3 = 23 / 3 = 7,67
Важно проговорить, что среднее арифметическое не может достоверно описать данные, если в них есть выбросы. В таких случаях более репрезентативными показателями будут медиана, мода или усеченное среднее.
Медиана
Медиана — это числовое значение, которое делит данные на две половины:
- 50% данных находятся выше медианы
- Остальные 50% — ниже
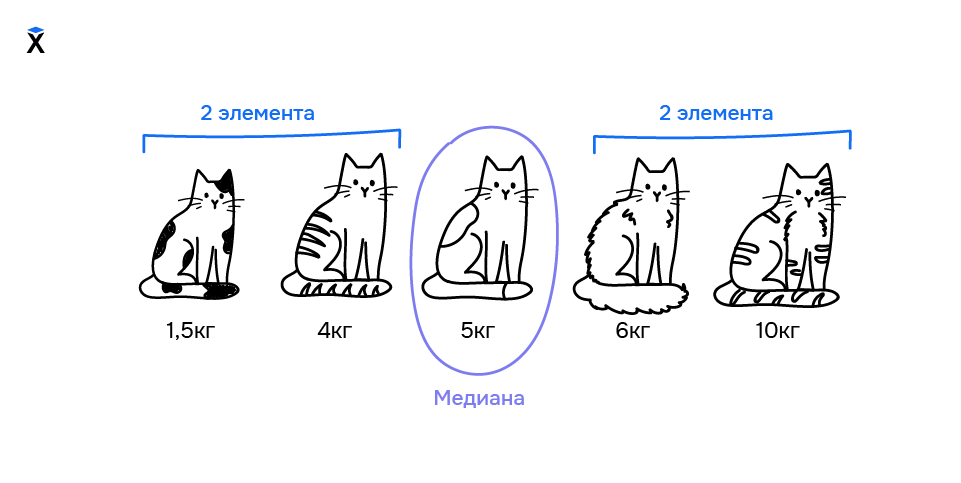
Медиана часто используется в статистике вместо среднего значения, если в данных есть выбросы. Чтобы найти медиану, нужно упорядочить все числа по возрастанию или убыванию, а затем выбрать серединное значение. Рассмотрим такой пример:
- Возьмем для примера выборку чисел
4, 6, 9, 12, 8 - Упорядочим числа по возрастанию —
4, 6, 8, 9, 12 - Найдем середину выборки — это будет третий из пяти элементов, то есть число
8
Если в выборке четное количество элементов медианой считается среднее число между двумя значениями по середине:
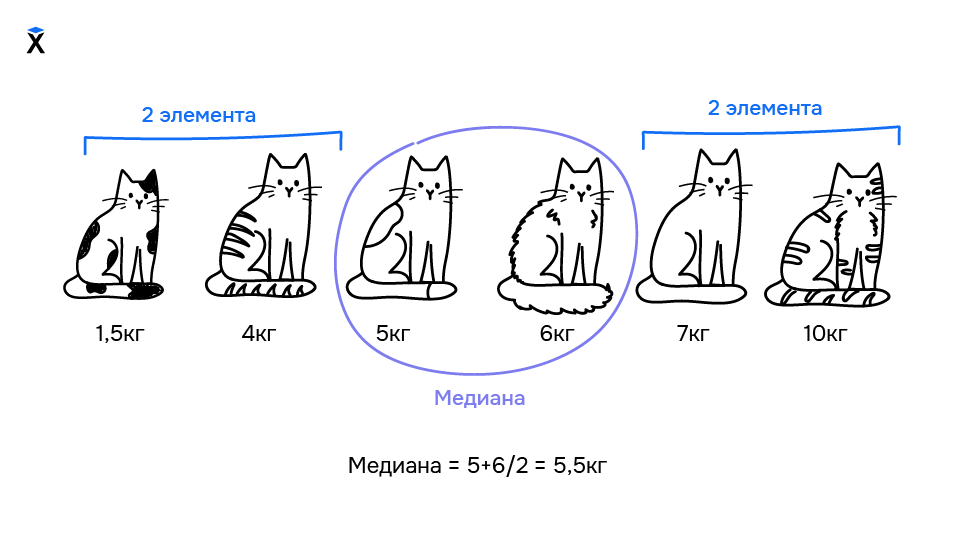
- Возьмем выборку
4, 6, 1, 9, 12, 8 - Упорядочим числа по возрастанию —
1, 4, 6, 8, 9, 12 - Найдем два элемента посередине —
6, 8 - Вычислим среднее между ними и получим число
7, это и есть медиана
В отличие от среднего значения, медиана не чувствительна к выбросам — экстремально высоким или низким значениям. Она не изменится, если добавить выбросы, которые могут исказить среднее значение. Еще медиана определяет центр распределения, потому что она является точкой, которая делит распределение пополам.
Мода
Мода — это самое частое значение в наборе чисел. В отличие от среднего значения или медианы, мода может быть не единственным значением в наборе данных. Например, если автосалон продал одинаковое количество автомобилей двух разных марок, то модой будут обе марки.
При этом мода не всегда репрезентативна:
- При очень маленькой выборке модой может быть значение, которое встретилось всего один раз
- При большом объеме выбросов модой могут быть значения, которые встречаются не так часто
- При небольшой разнице между значениями модой может стать несколько значений
Как выбрать метрику
Выбор статистического показателя зависит от того, какую информацию вы хотите получить. Среднее арифметическое помогает определить средний уровень, а медиана — типичный. Чтобы правильно выбрать метрику нужно определить, насколько однородны или разнородны числа в наборе. В этом помогают дисперсия и стандартное отклонение.
Возьмем для примера средний доход обычной семьи и Илона Маска за год. Допустим, что средний доход семьи составляет 50,000, а зарплата Илона Маска —22,500,000. Если мы возьмем среднее арифметическое от этих двух величин, то получим завышенное число для семьи и заниженное для Маска. Это число бесполезно, потому что оно не показывает реальный доход в обоих случаях.
Эффект длинных хвостов
Эффект длинных хвостов — это стратегия продаж, в которой много непопулярных продуктов приносят прибыль, сопоставимую с продажами популярных товаров.
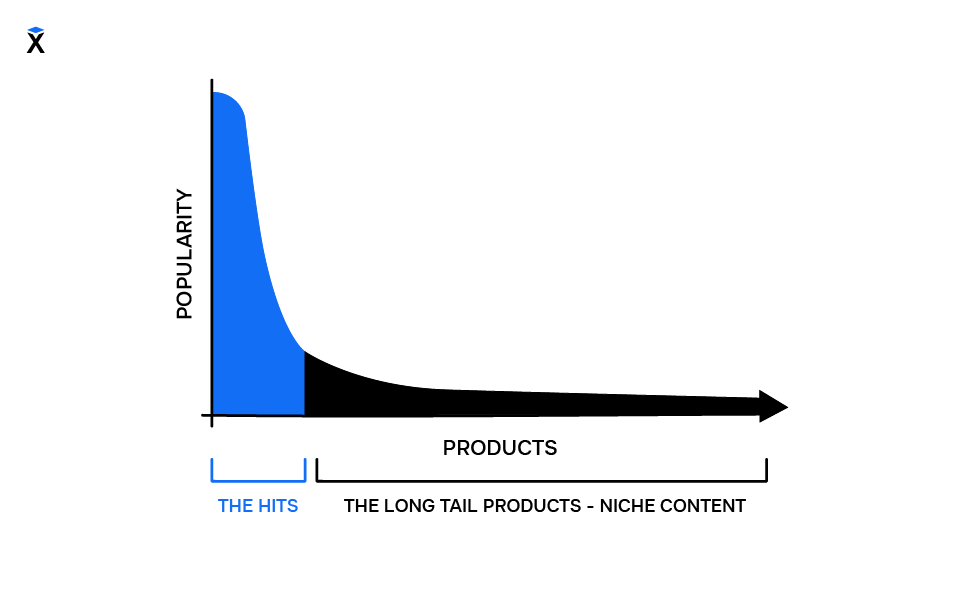
Другими словами, хвост из десятков нишевых товаров может приносить бизнесу столько же денег, сколько приносит хит — один популярный товар. Хиты и хвост различаются по популярности, поэтому их удобно сравнивать медианой объема продаж.
Выводы
Повторим ключевые выводы урока:
- Среднее арифметическое хорошо описывает наиболее типичное значение в наборе данных
- При этом оно не может достоверно описать данные, если в них есть выбросы
- Если в данных есть выбросы, лучше описывать набор данных при помощи медианы
Дополнительные материалы
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
