Точки — Python: Составные данные

В этом уроке мы начнем проектирование библиотек для работы с графическими примитивами (точками, отрезками), а также фигурами (кругами, прямоугольниками). Естественно, проще всего начать с основы — библиотеки для работы с точками. Для этого давайте вспомним координатную плоскость и то, как определяются на ней точки.

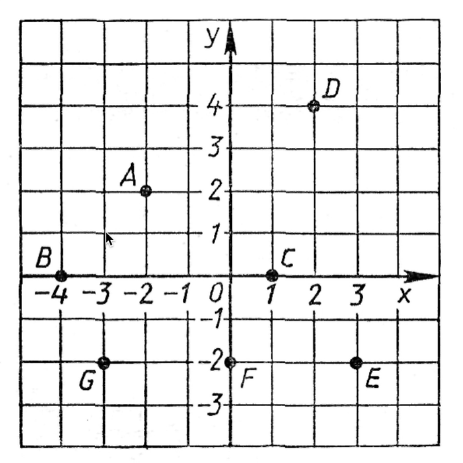
В этом примере мы видим плоскость, на которой расположены две оси (ось абсцисс X и ось ординат Y) и точки. При этом обычно точка описывается двумя параметрами: первым указывается координата x (абсцисса), вторым — координата y (ордината). Например, точка D описывается как (2, 4), точка C — (1, 0) и так далее. Координаты могут быть отрицательными. Оси делят плоскость на четыре части, которые называются квадрантами. На рисунке точка D лежит в первом квадранте, точки A, G, E — во втором, в третьем и в четвертом квадрантах соответственно.

Когда мы говорим о точках, мы на самом деле имеем в виду так называемые абстрактные данные. Это означает, что мы не делаем никаких предположений (кроме самых необходимых) для того, чтобы рассуждать в терминах этих данных (в нашем случае — точек).

Вспомним любой раздел школьной математики. Когда мы оперируем какими-то понятиями, мы вообще не думаем, как они должны быть представлены — мы мыслим в них на абстрактном уровне. Это позволяет нам строить законы, делать выводы и предположения о том, как будут вести себя данные, как они друг с другом комбинируются. При этом нам не нужна никакая реализация, не нужен ни язык программирования, ни компьютер. Более того, нам вообще необязательно графически изображать эти данные — мы можем представлять это в голове и при этом делать выводы, имеющие практическое значение.

При этом конкретные данные определяются условиями прикладного использования — например, особенностями разных языков программирования. Зачастую библиотеки снаружи выглядят одинаково и оперируют одними и теми же понятиями, но внутри устроены совершенно по-разному. Естественно, при манипуляциях с такими библиотеками необходимо оставаться в рамках понятийного аппарата тех абстрактных данных, с которыми мы работаем. Клеем между абстрактными данными и конкретными данными выступает интерфейс — это набор функций, обычно разделяемых на конструкторы и селекторы. Конструкторы позволяют из набора данных строить составной объект, а с помощью селекторов из составного объекта извлекают его части. В нашем случае, если говорить о точках, селекторы позволяют извлекать координаты x и y. Вот как выглядит интерфейс нашей библиотеки:

x = 5
y = -7

# Конструктор
point = make_point(x, y)

# Селекторы
get_x(point)
get_y(point)

to_string(point)  # (5, -7)

В коде выше видно, что мы определили функцию make_point(), которая принимает на вход два числа (x и y) и возвращает точку с такими координатами. Кроме этого, есть два основных селектора get_x() и get_y(), которые возвращают соответствующие координаты из точки. При проектировании библиотеки мы используем стратегию «мечтать не вредно», потому что еще не знаем, как она будет устроена внутри. Это, по большому счету, не имеет значения, потому что мы пользуемся абстрактными данными и оперируем терминами нашей предметной области, а не конкретной реализации. Поэтому мы можем сосредоточиться на сути, отложив принятие решения о деталях.

Кроме основных селекторов, нами определена функция to_string(), которая возвращает текстовое представление точки и может быть использована для отладки.

Давайте посмотрим, какие манипуляции можно производить над точками, имея базовый интерфейс:

def symmetrical_point(point):
    return make_point(get_x(point), -get_y(point))

point = make_point(10, 10)

symmetrical_point(point)  # (10, -10)

В примере выше определена функция symmetrical_point(), которая возвращает точку, симметричную заданной относительно оси X. Например, для точки c координатами (10, 10) функция вернет точку с координатами (10, -10). Функция устроена следующим образом: с помощью селекторов мы извлекаем координаты, инвертируем координату Y и создаем новую точку с помощью конструктора make_point(). Большинство операций с точками состоят в том, чтобы извлечь координаты, произвести с ними необходимые изменения и создать новые точки. С помощью этого нехитрого алгоритма можно реализовать массу других функций, например:

point = make_point(3, 4)
point2 = make_point(0, 0)

get_quadrant(point)  # 1
get_distance(point, point2)  # 5

Функция get_quadrant() определяет квадрант, в котором расположена точка, а функция get_distance() вычисляет расстояние между заданными точками. При этом мы оперируем понятием "точки", а обращение к составным частям этих точек происходит внутри и скрыто от наших глаз.

Подведем итог:

Абстрактными данными у нас является точка, которая характеризуется двумя значениями (координатами) x и y.

Конкретные данные: на текущий момент мы не знаем, как реализованы точки (что не мешает нам пользоваться библиотекой в рамках нашей предметной области).

Интерфейс:

# Конструктор
make_point(<x>, <y>)

# Селекторы
get_x(<point>)
get_y(<point>)

Внутренняя реализация

point = make_point(4, 5)

print(get_x(point))
print(get_y(point))

print(point) # don't do it
print(to_string(point))
print(get_quadrant(point))

Если вас мучает вопрос, что находится внутри переменной point, скажу сразу — мы ответим на него в следующих уроках. Для работы с точками не нужно знать их устройство. Когда мы решаем геометрические задачи, то легко оперируем понятием отрезка, круга и других фигур. С помощью формул мы можем находить площадь, рассчитывать расстояние между точками, проводить касательные и делать многое другое.

Каждое из перечисленных выше понятий абстрактно, не имеет прямого воплощения в реальной жизни и может применяться как к описанию детских игрушек (круглый мяч), так и египетских пирамид. Причем в каждом конкретном случае нас будут интересовать разные детали. В одних случаях важны только размеры, в других — расположение относительно некоей системы координат, в третьих — цвет фигуры.

В некоторых задачах при работе с точками могут отсутствовать координаты, но имеются цвет или скорость мерцания. Тогда набор функций для работы с подобными точками будет кардинально отличаться от нашего набора.

Точки, которые мы рассматриваем в этом курсе, интересны для нас только как место на координатной плоскости, задаваемое парой чисел — координат. Важно, что любая пара чисел однозначно определяет точку на этой плоскости, и существование двух разных точек с одинаковыми координатами невозможно.

Точки — это всего лишь один из примеров того, как мы пытаемся выразить в коде нашу предметную область, в данном случае — геометрию. Подобная абстракция используется в исходном коде графических редакторов. В финансовых приложениях используется понятие "деньги". Деньги можно выразить просто числом, но этого наверняка будет недостаточно, потому что помимо численного значения, для выражения денежной суммы необходимо как минимум указать еще и валюту.

Можно сказать, что в коде выше создан свой собственный, пользовательский тип данных. В отличие от примитивных типов данных, таких как числа и строки, наш новый тип является составным — отсюда и понятие составные данные. Внутри себя он хранит набор значений, но мы оперируем им как единым целым.

Реальные прикладные приложения, по большей части, оперируют именно такими данными. Например, в Хекслете это уроки, курсы, практики, пользователи, наставники, топики в комьюнити, счета и сотни других понятий. Все они гораздо более сложные, чем те же точки. В одном пользователе могут находиться десятки параметров.

Невозможно заранее определить типы данных для представления всего сущего на земле. Все, что требуется от языка — предоставить возможность определять свои собственные типы и операции над ними. И об этом мы поговорим в следующем уроке.

Дополнительные материалы

1. Система координат

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты