Создание абстракции — Python: Абстракция с помощью данных

• Полярная система координат
• Скрываем внутреннюю структуру
• Выводы

Декартова система координат — не единственный способ графического описания. Другой способ — полярная система. В этом уроке мы познакомимся с ней и узнаем, чем она полезна. Также разберем, как скрывать внутреннюю структуру.

Полярная система координат

Полярная система координат — это способ представления точек на плоскости с помощью двух чисел: расстояния и угла. В отличие от декартовой системы координат, где используется пара чисел (x, y) для описания положения точки, в полярной системе используется радиус (r) и угол (φ):

• Радиус (r) — это расстояние от начала координат до точки. Значение радиуса всегда неотрицательное, так как это расстояние
• Угол (φ) — это угол между положительным направлением оси Х и линией, которая соединяет начало координат и точку. Угол измеряется в градусах (от 0 до 360) или радианах (от 0 до 2π)

Рассмотрим пример точки P на полярной системе координат:

Чтобы описать точку P в полярной системе координат, необходимо знать ее радиус и угол. Чтобы найти радиус, мы считаем расстояние от начала координат до нашей точки P — в нашем случае это радиус r равен 5.

Далее построим линию от центра координат до нашей точки P и найдем угол между положительным направлением оси Х и данной линией. В нашем случае угол φ равен 60°. Готовый результат записывается как P(5:60°).

Полярная система координат особенно удобна при решении задач, связанных с кругами, спиралями или симметрией относительно центра. В некоторых случаях она может упростить вычисления и формулы.

Например, точка с полярными координатами (r, φ) может быть представлена в декартовой системе координат с помощью следующих формул:

x = r * cos(φ)

y = r * sin(φ)

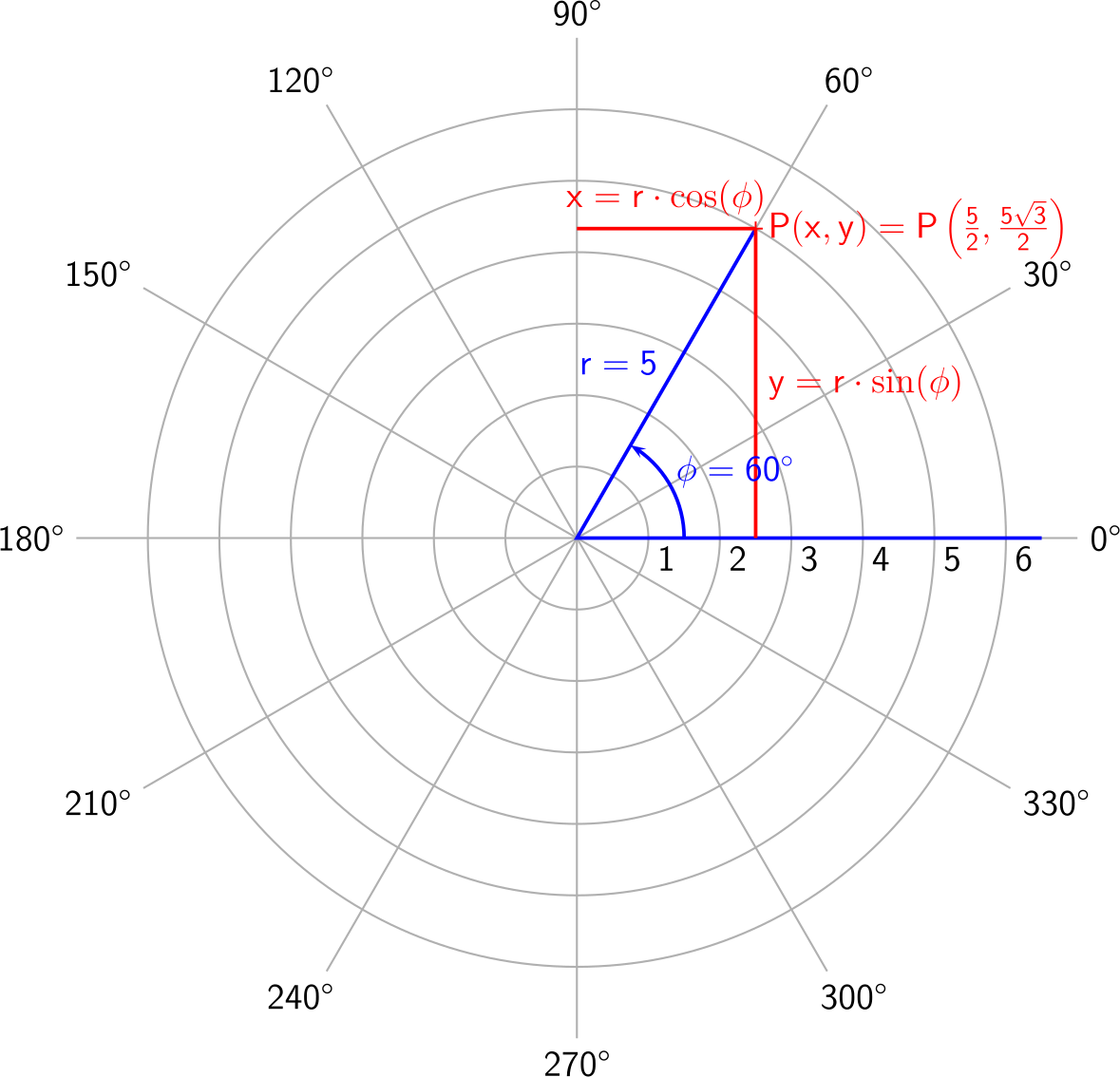
Если рассматривать наш предыдущий пример, то координаты точки P(5:60*°) в декартовой системе координат будут рассчитываться как P(5 * cos(60°), 5 * sin(60°*)).

Представим, что мы разрабатываем графический редактор по типу Photoshop. Библиотека для работы с графическими примитивами построена на базе декартовой системы координат. Мы понимаем, что переход на полярную систему поможет сделать работу проще и быстрее. Но для этого придется переписать практически весь код:

point = {"x": 2, "y": 3}
symmetrical_point = {
    "x": -point["x"],
    "y": point["y"],
}

Связано это с тем, что наша библиотека не скрывает внутреннюю структуру. Любой код, который использует точки или отрезки, знает о том, как они устроены внутри. Это относится как к коду, который создает новые примитивы, так и к коду, извлекающему из них составные части.

Скрываем внутреннюю структуру

Изменить ситуацию и спрятать реализацию можно с помощью функции:

point = make_point(3, 4)
symmetrical_point = make_point(-get_x(point), get_y(point))

В примере мы видим три функции: make_point(), get_x() и get_y():

• make_point() называется конструктором, потому что она создает новый примитив
• get_x и get_y называются селекторами или selector — от слова select. Это в переводе означает «извлекать» или «выбирать»

Такое небольшое изменение приведет к долгосрочным последствиям. Главное, что в прикладном коде, который использует библиотеку, нет работы со структурой напрямую:

# То есть мы работаем не так
point = [1, 4] # мы знаем, что это список
print(point[1]) # прямое обращение к списку

# А так
point = make_point(3, 4) # мы не знаем как устроена точка
print(get_y(point)) # мы получаем доступ к частям только через селекторы

Если посмотреть на этот код, нельзя сказать, что представляет точка изнутри, и какими конструкциями языка она представлена. Так мы построили абстракцию данных.

Суть абстракции заключается в том, что мы скрываем внутреннюю реализацию. То есть создание абстракции с помощью данных скрывает эти данные от внешнего кода.

Посмотрим на один из способов реализовать абстракцию для работы с точкой:

def make_point(x, y):
    return {"x": x, "y": y}

def get_x(point):
    return point["x"]

def get_y(point):
    return point["y"]

Теперь мы можем менять реализацию и не переписывать весь код. При этом иногда придется переписывать отдельные части кода.

В этом примере мы используем функцию make_point(), которая создает точку на основе декартовой системы координат. Она принимает на вход координаты x и y. При этом внутри она может представляться в полярной системе координат. Получается, что во время конструирования один формат транслируется в другой:

import math

def make_point(x, y):
    # конвертация
    return {
        "angle": math.atan2(y, x),
        "radius": math.sqrt(x ** 2 + y ** 2)
    }

Выводы

В этом уроке мы познакомились с полярной системой координат и узнали, чем она полезна. Также разобрали, как скрывать внутреннюю структуру.

Важно понимать, что после начала работы через абстракцию данных пути назад нет. Придерживайтесь всегда тех функций, которые вы создали сами. Либо тех, которые вам предоставляет используемая библиотека.

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты

Об обучении на Хекслете

• Статья «Как учиться и справляться с негативными мыслями»
• Статья «Ловушки обучения»
• Статья «Сложные простые задачи по программированию»
• Вебинар «Как самостоятельно учиться»