Представление последовательностей — JS: Последовательности

• Пары
• Способы соединить 1, 2, 3 и 4
• Что такое множество
• Замыкание (абстрактная алгебра)
• Последовательности
• Интерфейс
• Повышаем уровень абстракции

Пары

Наше погружение в последовательности мы начнём с того, что проработаем уровень абстракции для работы со списками. Давайте вспомним, как работают пары. С помощью пар, а конкретно функции-конструктора cons, мы можем соединять, например, числа:

import { cons, toString } from 'hexlet-pairs';

cons(5, 8);

const pair = cons(5, cons(2, 9));

Также можем соединять любые объекты данных, включая те же пары. В данном примере мы соединяем 5 как число и другую пару. Если мы распечатаем, то увидим, что у пары такое представление:

toString(pair); // (5, (2, 9))

https://repl.it/@hexlet/js-sequences-list-cons

Способы соединить 1, 2, 3 и 4

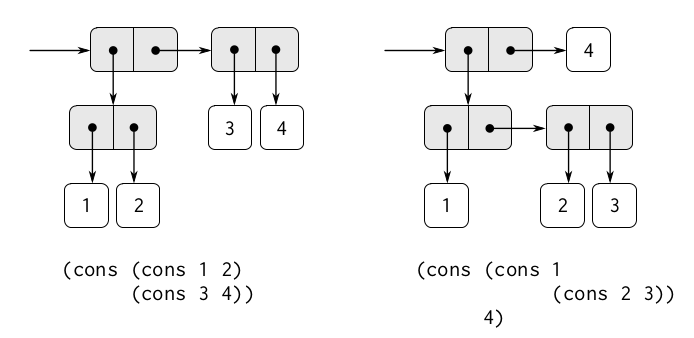
Существует более одного способа соединять различные числа, т.е. представлять их разными структурами данных. Например, числа 1, 2, 3, 4 можно соединить в единую иерархическую конструкцию, как на примере слева на так называемой стрелочной диаграмме. Мы видим, что в паре на самом верху левый элемент является парой, правый — тоже пара и в каждой из этих пар элементы представлены конкретными числами.

При этом может быть и совершенно другой вариант, в котором левый элемент является парой, а правый, например, является числом 4. Левый элемент в свою очередь делится на элемент, в котором есть число и элемент, являющийся парой и т.д. Мы можем это делать бесконечно много раз.

Под диаграммами описано представление в виде кода с помощью вложенных cons. Причём слева симметричное вложение, а справа немного сдвинутое.

То, что мы получили, называется — иерархической структурой. Её создание обеспечивается возможностью, которая называется — свойство замыкания (множества). Чтобы понять, что это обозначает, давайте познакомимся с понятием множества.

Что такое множество

Множество — это довольно интуитивное понятие. Для математики оно является одним из ключевых. Через множество определено большое количество вещей. Определение чистых математических функций, с которыми мы работаем, полностью построено на теоретико-множественном подходе. Так вот, что такое множество? Множество — это какой-то набор. Мы можем сказать, что это совокупность объектов данных. Например, в данном случае мы видим, что это различные типы чисел. При этом множества вложены друг в друга, т.е. у множеств есть отношения друг с другом. Существуют операции над множествами, например: пересечение, объединение и т.д. Причём это не просто какая-то математическая теория. Множества очень активно используются в практике программирования. Те же самые базы данных SQL основаны на реляционной алгебре, которая очень тесно связанна с теорией множеств. Например, "джойны", которые используются в SQL следует воспринимать и анализировать именно на основе понимания теории множеств.

Поскольку мы говорим о парах, мы можем себе представить некоторое множество — множество всех пар. Далее нам это понадобится.

Замыкание (абстрактная алгебра)

Это не то замыкание, про которое мы уже говорили, связанное с запоминанием контекста. Это замыкание из математики, из абстрактной алгебры и звучит оно примерно так:

Множество замкнуто относительно операции, если применение операции к элементам этого множества даёт результат, который также является элементом этого множества.

Возможно, это слишком формальное определение, которое звучит очень абстрактно. На самом деле оно крайне простое. Всё, что оно означает: используя функцию cons, множество всех пар замкнуто относительно функции cons. Почему? Потому что когда вы с помощью функции cons что-либо объединяете, вы снова получаете пару. Если полученную пару объединить функцией cons в ещё одну пару, получится, опять же, пара. Но как мы помним, множество всех пар включает все возможные виды пар. Какую бы пару вы ни создали, она будет туда включена, таким образом функция cons всегда порождает пару. Если бы в какой-то момент она порождала что-то другое, то не существовало бы замкнутости. Замкнутость присутствует именно потому, что применение этой функции к абсолютно любым элементам данного множества порождает элемент этого же множества. А свойство замыкания является ключевым фактором в возможности построения иерархических структур.

Иерархические структуры — это такие структуры, части которых содержат в себе ещё более элементарные части, которые в свою очередь содержат ещё более элементарные части.

cons(cons(3, 5), cons(2, 9));

В примере выше cons соединяет не элементарные части. Она соединяет пары, которые в свою очередь состоят из частей и так далее. Это может происходить бесконечно, благодаря свойству замыкания.

Последовательности

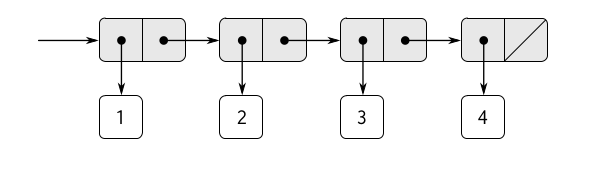
Как же всё-таки проще всего представить последовательности? Мы используем стрелочную диаграмму, которая показывает самый простой, но не единственный способ представления последовательностей. На верхнем уровне у нас находится пара, первый элемент которой объект данных, например, число, второй элемент — это ссылка на другую пару, в которой опять же первый элемент — объект данных и дальше опять ссылка на следующую пару. И так далее до самой последней вложенной пары, где первый элемент — данные, а второй элемент - специальный маркер, который обозначает, что список закончился, и дальше смотреть не нужно.

Как это записывается кодом? По сути — это последовательность cons'ов, которые вложены друг в друга.

cons(1,
  cons(2,
    cons(3,
      cons(4, null))));

Мы приняли за аксиоматический факт, что у последнего элемента маркер окончания списка это null. Если мы его встречаем значит дальше можно не смотреть, список закончился.

Интерфейс

import {
l, cons, head, tail, isEmpty, toString
} from 'hexlet-pairs-data';

// cons(1, cons(2, cons(3, cons(4, null))));
const list = l(1, 2, 3, 4);

cons(10, list); // (10, 1, 2, 3, 4)
toString(list); // (1, 2, 3, 4)

head(list); // 1
tail(list); // l(2, 3, 4)

// list === null
isEmpty(l(4)); // false
isEmpty(l()); // true

https://repl.it/@hexlet/js-sequences-list-interface

Давайте рассмотрим интерфейс работы со списками. Начиная с текущего момента и на протяжении всего курса, мы будем постоянно с ними работать, строить поверх них абстракции. Поэтому нам нужно научиться выполнять какие-то базовые операции со списками и построить данный слой абстракции поверх пар.

Если бы мы действовали в лоб, то создание списка выглядело бы так:

cons(1, cons(2, cons(3, cons(4, null))));

Но как видите, это довольно громоздкая запись, здесь слишком много "шума" и сложно увидеть реальную структуру списка, а ведь список состоит всего из четырёх чисел. Поэтому мы сделали функцию-конструктор для создания списков:

const list = l(1, 2, 3, 4);

Эта функция принимает на вход числа через запятую и возвращает список. Т.е. внутри она делает то же самое, что описывает код выше. Функция l работает с переменным числом аргументов (оно не задано жёстко и вы можете передавать любое количество). Внутри она имеет кое-какие особенности, с которыми мы ещё не знакомы и чтобы понять её устройство нужно продвинуться вперёд гораздо дальше. Поэтому просто используйте данную функцию, как чёрный ящик, представляя, что вызывая конструктор l(1, ...) вы получаете запись cons(1, ...).

Почему мы сделали именно так и назвали конструктор l одной буквой? Всё очень просто. Потому что мы часто будем строить вложенные списки и это очень просто делать, если у вас короткое название функции. Кстати, если бы оно было длинное, то вложенные функции банально привели бы к распуханию этой структуры. При этом для добавления элемента в список мы используем функцию cons. Но эта функция будет определена уже в списках, т.е. она не является функцией пар, так как это другой слой абстракции. Если мы посмотрим на внутреннюю структуру, то увидим следующее:

cons(10, list); // (10, 1, 2, 3, 4)

Если распечатать список, то можно увидеть, что десятки здесь уже нет:

toString(list); // (1, 2, 3, 4)

Это означает, что у нас присутствует неизменяемость. Добавление в список, как это было с парами, не изменяет его, а возвращает новый список. Поэтому, если вы хотите его использовать, то необходимо создать константу, например, list2.

И ещё несколько базовых операций, которые обязательно будут нужны для работы со списками. Они очень похожи на car и cdr. Первая из них — это head, так называемая голова. Данная функция берёт из списка первый элемент. Когда идёт работа со списками, существует понятийный аппарат, в котором есть и данное определение.

Первый элемент списка (т.е. последний добавленный) называется "голова", а всё остальное — это хвост. Соответственно, head — это взять голову, tail — это взять хвост. Хвост — это список минус первый элемент. Мы говорим первый, так как он находится всегда слева, но по сути это то, что добавляется в список последним. В данном случае tail(list), учитывая, что наш список был l(1, 2, 3, 4), это список l(2, 3, 4). Если мы будем применять к списку tail много раз, то постепенно будем получать список меньшего размера, пока в конце концов не получим null.

Ещё одна функция — это isEmpty. Она проверяет пустой ли список, т.е. внутри она делает такую проверку:

// list === null
isEmpty(l(4)); // false
isEmpty(l()); // true

Видно, что если мы передаём просто конструктор, вызванный без параметров, то isEmpty считает, что это пустой список. Если хотя бы один параметр был передан, то список уже не пустой.

Почему мы не делаем такую проверку list === null, а вводим новую функцию? Думаю вам уже должно быть понятно. Мы ведь всё время говорим о том, что необходимо использовать абстракцию. То, что внутри используется null — это всего лишь особенность реализации. Сегодня null, завтра что-то ещё. И если вы используете те функции, которые предоставляет библиотека, вам не придётся в будущем переписывать весь код.

Повышаем уровень абстракции

В этом уроке мы реализовали абстрактный тип данных Список на основе ранее пройденных пар. Ключевой особенностью списка является его интерфейс, а именно функции, реализующие такие операции, как "получить голову" (возвращает первый элемент списка), "получить хвост" (возвращает новый список, полученный из исходного списка отсечением у него первого элемента), "добавить новую голову" (добавление элемента в начало списка). И здесь следует обратить внимание на несколько вещей.

Во-первых, не стоит отождествлять между собой пары и списки. Пары в данном случае были использованы как подходящий инструмент для создания списка. Абстрактный список (см. первый абзац) может быть реализован в конкретных структурах данных. В нашем случае это односвязный список. Важной характеристикой этой структуры данных является то, что каждый элемент списка, помимо определённого хранимого значения (число, строка, дата, адрес, имя и любая другая информация), содержит ссылку на другой такой же по структуре элемент. Таким образом, между элементами списка существует связь, и мы можем последовательно "путешествовать" (перемещаться) от текущего элемента к следующему, от начала списка к его концу.

И, как видим, пары вполне позволяют реализовать особенности списка как структуры данных. Ведь пара, помимо основного значения, может содержать ещё другую пару аналогичной структуры (значение + ссылка на другую пару) — и такая последовательность может длиться бесконечно.

cons(1, cons(2, cons(3, cons(4, cons(5, ...
cons('one', cons('two', cons('three', cons('four', cons('five', ...

Однако, надо понимать, что сделать это можно не только с помощью пар. Cписки можно представить на основе массивов, а также некоторых других типов данных. Поэтому, если мы пользуемся списком, то к нему нельзя напрямую применять функции по работе с парами даже если мы знаем, что данный конкретный список состоит из пар. Для этого вводятся специальные функции для работы со списками, учитывающие его внутреннюю реализацию, которая может изменяться.

Во-вторых, коль скоро мы реализовали список именно на основе пар, то следует понимать, что не каждая пара, с которой мы имеем дело, какой бы «сложной» она ни была, является списком. У списка есть начало и конец, и мы должны иметь возможность последовательно перемещаться от одного элемента к другому. Для того, чтобы понять, что мы достигли последнего элемента списка и перемещаться дальше уже нет смысла, мы вводим специальный маркер конца списка — пустую пару l(). По предварительному соглашению в роли маркера могут также выступать другие подходящие значения, например, null. Как только мы встречаем очередную пару, в cdr которой находится пустая пара, это означает, что очередное значение списка, лежащее в car пары, является последним элементом списка. Отметим также, что у пустого списка (списка, в котором нет ни одного элемента) не может быть ни головы, ни хвоста. Поэтому соответствующие операции, примененные к пустому списку (взятие head или tail), приводят к возникновению ошибки. Чтобы её избежать, вводят функцию для проверки списка на «пустоту» (например, isEmpty), а далее берут голову или хвост у списка, предварительно убедившись, что он не является пустым.

Ниже приведены примеры пар, которые нельзя назвать списками. Они не реализуют требования, предъявляемые к односвязным спискам: в них отсутствует последовательная связь между элементами и/или нет маркера конца списка:

cons(1, cons(cons(3, null), 2));
cons(1, cons(2, cons(3, 4)));
cons(cons(1, 2), cons(3, cons(4, null)));

Теперь покажем пары, которыми мы можем смело пользоваться как списками:

cons(1, cons(2, cons(3, null)));
cons('This', cons('is', cons('a', cons('list', null))));

В уроке мы отметили, что следующие две записи, конструирующие список, являются эквивалентными:

cons(1, cons(2, cons(3, cons(4, cons(5, null))))); // (1, 2, 3, 4, 5)
l(1, 2, 3, 4, 5); // (1, 2, 3, 4, 5)

Для генерации списка мы создали функцию l, несмотря на то, что у нас уже есть конструктор cons. Это необходимо по нескольким причинам. Отметим наиболее важные из них:

• Выделив код создания списка в отдельную функцию и дав ей имя l (сокращ. от list), мы ввели отдельную и понятную абстракцию, отвечающую за создание списков (и ничего другого!). Выше говорилось, что списки могут быть реализованы не только на парах, но и на массивах, а также других типах данных. Так вот, наша абстракция l позволяет отвлечься от внутреннего устройства списка. Тот, кто будет пользоваться этой функцией, не обязан знать, какими способами она конструирует список, а в случае необходимости может изменить его внутреннее устройство "незаметно и безболезненно" для пользователей l.
• Хорошая абстракция делает код более понятным и повышает его читабельность. Теперь, видя в коде l, мы однозначно понимаем, что здесь происходит. Тогда как в ином случае, цепляясь глазом за множественные, разбросанные среди строк cons, мы каждый раз должны будем определять, что же делает данная конкретная пара: то ли создаёт список, то ли хранит временные данные, то ли печёт пирожки ?! ;)

Посмотрите на «безликие» нагромождения пар, создающие разные сущности, которые мы проходили в прошлых курсах. Только комментарии помогают понять, что здесь происходит.

cons(5, cons(2, cons(7, cons(11, cons(6, cons(14, null)))))); // создание списка
cons(3, 17); // создание точки
cons(8, 17); // создание рационального числа
cons(cons(3, 33), cons(-2, -22)); // создание отрезка
const rectangle = cons(cons(-2, 23), cons(5, 11)); // создание прямоугольника
2 * (car(cdr(rectangle)) + cdr(cdr(rectangle))); // вычисление периметра прямоугольника

А вот как выглядит код с введёнными абстракциями. Комментарии здесь уже не нужны:

list(5, 2, 7, 11, 6, 14);
makePoint(3, 17);
makeRational(8, 17);
makeSegment(makePoint(3, 33), makePoint(-2, -22));
const point = makePoint(-2, 23);
const rectangle = makeRectangle(point, 5, 11);
perimeter(rectangle);

Естественно, введение функции устраняет дублирование кода. Каждый раз писать при создании списка такое нагромождение кода в виде вложенных cons, демонстрируя при этом все внутренности создаваемой конструкции, — не лучший стиль написания кода.

const { l, head, tail } = require('@hexlet/pairs-data');

const list = l(5, 3, 9);
console.log(head(tail(list))); // => 3

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты