Алгоритм Дейкстры

Алгоритм Дейкстры - это алгоритм для нахождения кратчайших путей в графе с положительными весами рёбер.

Алгоритм Дейкстры может использоваться для решения различных задач, связанных с оптимизацией маршрутов, распределением ресурсов и другими проблемами, которые можно представить в виде графа. Например, его можно использовать для определения оптимального маршрута между двумя точками в сети, планирования маршрутов доставки, оптимизации загрузки серверов и многих других задач.

Алгоритм Дейкстры — это алгоритм, который находит кратчайшие пути от одной заданной вершины до всех остальных вершин во взвешенном графе

Граф — это набор вершин и ребер. Вершины описывают объекты, ребра — связи между ними. У каждого ребра есть вес. Вес задает стоимость перехода: расстояние, время, цену, расход энергии. Алгоритм применим только тогда, когда все веса ребер неотрицательные. При отрицательных весах результат может быть неверным.

Алгоритм вычисляет не один маршрут «из A в B», а минимальные расстояния от источника ко всем достижимым вершинам. При сохранении предшественников можно восстановить сами пути.

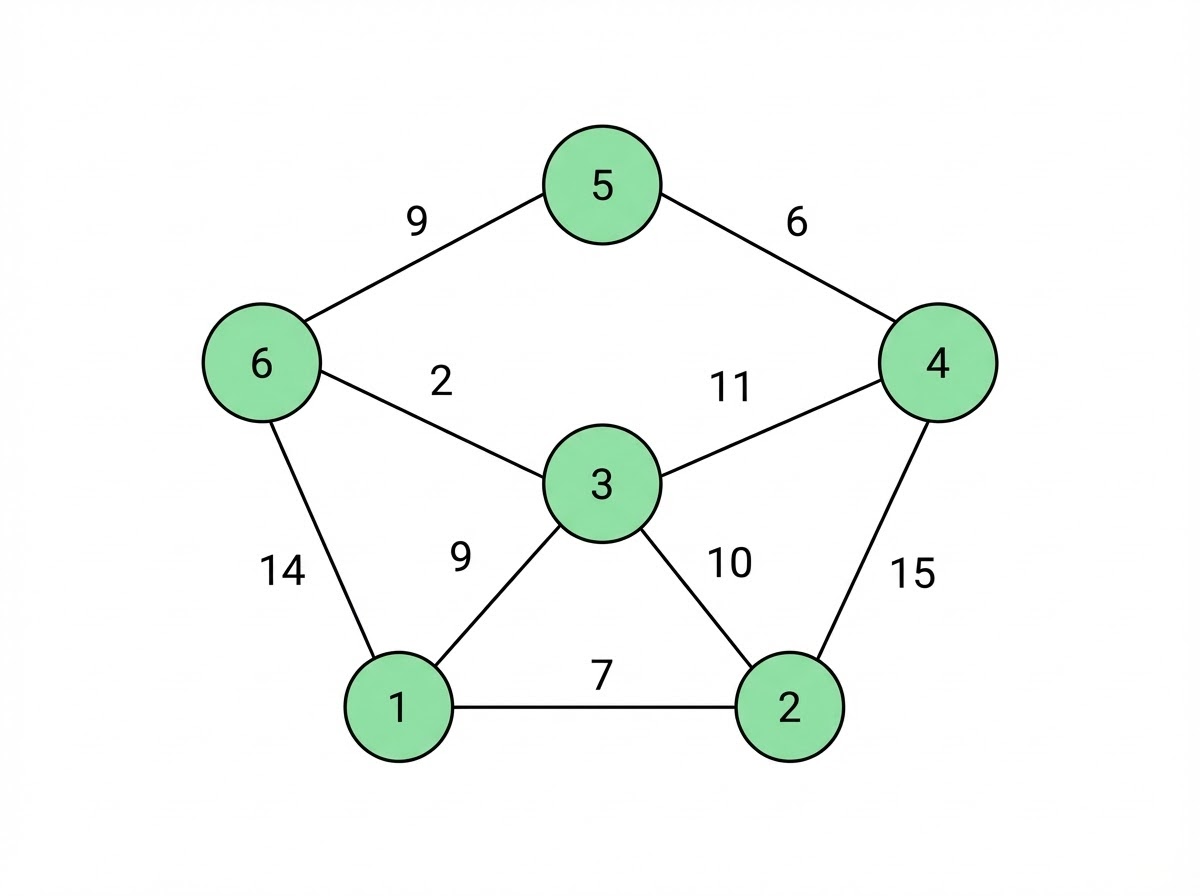
Где используют алгоритм

Алгоритм подходит для задач, где систему удобно представить графом, а цель — минимизировать суммарную стоимость:

• построение маршрутов на картах и в навигации;

• выбор оптимальных пересадок в транспортных сервисах;

• маршрутизация в сетях передачи данных;

• планирование движения роботов и автономных устройств;

• поиск пути и принятие решений в игровом ИИ;

• анализ потоков в инженерных моделях и схемах.

В каждом случае меняется смысл веса, но правило одно: суммируется стоимость пройденных ребер.

Как работает алгоритм

Алгоритм выполняется шаг за шагом. Он поддерживает текущие оценки расстояний от источника и постепенно «закрепляет» вершины с уже найденным минимальным расстоянием.

Состояния, которые используются в процессе:

• метка расстояния для каждой вершины (лучшее найденное значение);

• признак обработанности вершины;

• при необходимости — массив предшественников для восстановления маршрута.

Шаги выполнения

1. Инициализация

   Источнику присваивается 0. Остальным вершинам присваивается бесконечность. Все вершины считаются необработанными.

2. Выбор вершины

   Среди необработанных выбирается вершина с минимальной меткой расстояния. Она становится текущей.

3. Релаксация ребер

   Для каждого соседа текущей вершины считается новая длина пути:

   dist[current] + weight(current, neighbor)

   Если новое значение меньше текущей метки соседа, метка обновляется. При восстановлении пути также обновляется предшественник.

4. Фиксация

   Текущая вершина помечается обработанной. Ее метка больше не изменяется.

   Цикл повторяется, пока есть необработанные вершины с конечной меткой. Если вершина остается с бесконечностью, она недостижима из источника.

Что получается на выходе

Результат работы — минимальные расстояния от источника:

• до каждой достижимой вершины есть численное значение стоимости пути;

• при хранении предшественников можно восстановить конкретный маршрут.

Слово «расстояние» условное. В роли веса часто используют:

• время прохождения;

• стоимость;

• задержку в сети;

• расход энергии;

• штраф или риск.

Ограничения и важные условия

Алгоритм Дейкстры требует неотрицательных весов. При наличии отрицательных ребер нужно применять другие методы. Точность результата зависит не от данных, а от соблюдения условия по весам. Эффективность реализации зависит от структуры графа и выбранных структур данных, поэтому для больших графов используют приоритетные очереди.