АВЛ-дерево

АВЛ-дерево — это бинарное дерево поиска, которое автоматически сохраняет баланс: у каждого узла разница высот левого и правого поддеревьев не превышает 1. За счет этого поиск, добавление и удаление элементов выполняются за время порядка log(n).

Название структуры образовано от фамилий ее авторов — Адельсона-Вельского и Ландиса. По сути, это классическое BST, в котором добавлен строгий контроль высоты ветвей, чтобы дерево не становилось слишком «вытянутым».

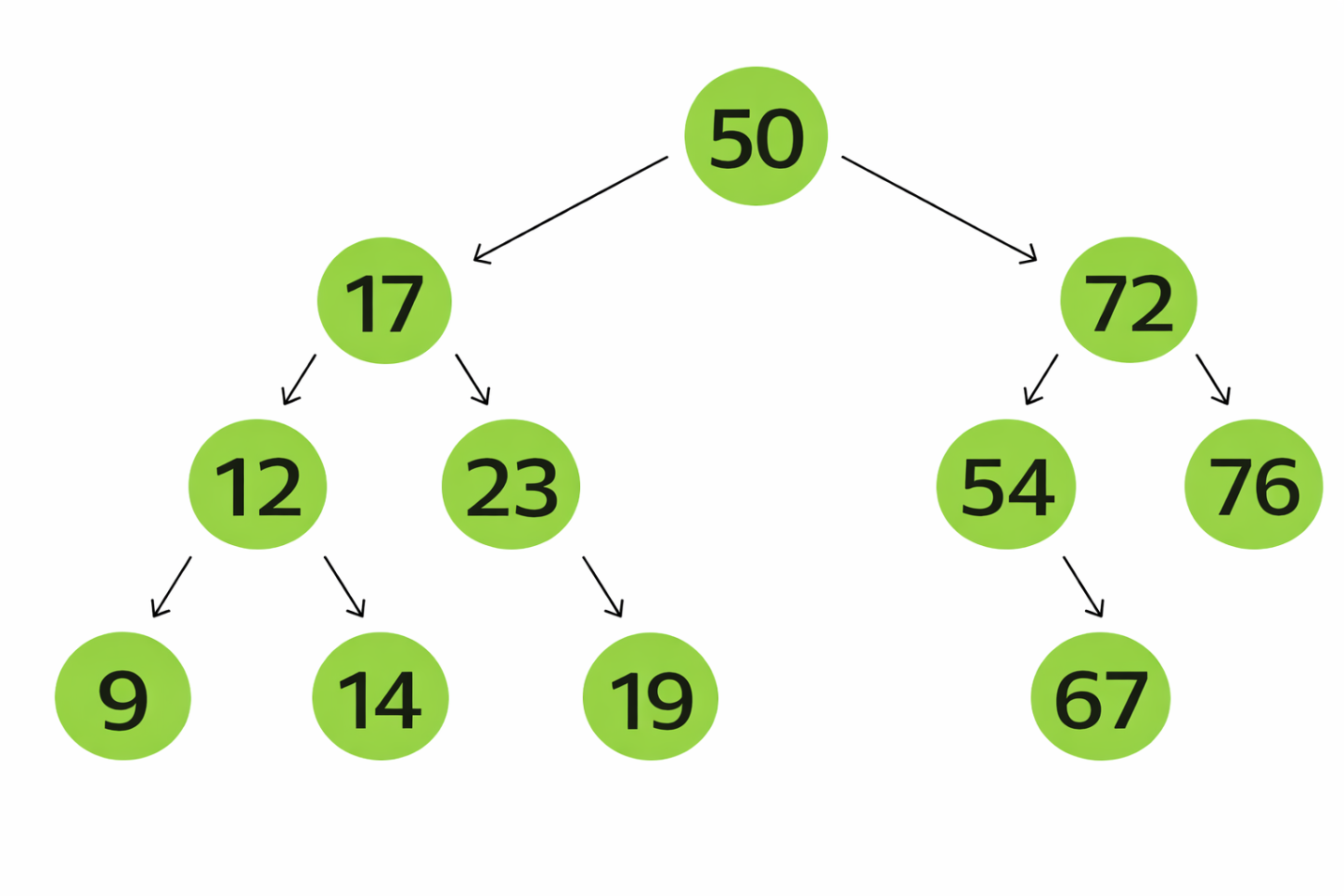
Что такое бинарное дерево поиска

Это иерархическая структура из узлов, где у каждого может быть до двух потомков: левый и правый.

Бинарное дерево поиска отличается от обычного бинарного дерева правилами размещения значений:

• значения в левом поддереве меньше значения узла;

• значения в правом поддереве больше или равны значению узла;

• правило выполняется для каждого узла и его поддеревьев.

Эти свойства позволяют выполнять поиск без полного перебора элементов.

Проблема вырождения дерева

Обычное бинарное дерево поиска не гарантирует хорошую форму. При неудачной последовательности вставок дерево может стать несбалансированным. В крайнем случае возникает вырождение: каждый узел имеет только одного потомка. Структура превращается в цепочку.

Последствия вырождения:

• поиск становится линейным по времени;

• вставка и удаление также переходят к линейной сложности;

• эффективность структуры падает до уровня связанного списка.

АВЛ-дерево создано для предотвращения такого сценария.

Для чего используют АВЛ-деревья

АВЛ-деревья применяются там, где нужно хранить множество элементов и быстро работать с ними по ключу. Их используют в программных системах, которые требуют предсказуемого времени операций.

Основные задачи, где полезна структура:

• хранение отсортированных данных в памяти;

• быстрый поиск по ключу;

• проверка существования элемента;

• вставка и удаление без деградации производительности;

• построение более сложных структур данных.

АВЛ-дерево подходит, если важна стабильность скорости операций, а не только средняя производительность.

Кто работает с АВЛ-деревьями

Структура встречается в разных областях разработки и анализа данных. С ней работают специалисты, которые проектируют алгоритмы и внутренние механизмы программ.

Типичные пользователи структуры:

• разработчики, реализующие алгоритмы поиска и сортировки;

• инженеры, работающие с индексами и структурами хранения;

• аналитики данных, которым требуется быстрый доступ к элементам по значению;

• специалисты по дискретной математике и теории графов.

Знание принципов работы АВЛ-дерева часто проверяют на технических собеседованиях.

Чем АВЛ-дерево отличается от обычного BST

АВЛ-дерево сохраняет правила бинарного дерева поиска, но добавляет ограничение по высоте. Главное отличие — контроль баланса.

Ключевые отличия АВЛ-дерева:

• баланс поддерживается строго по высоте;

• разница высот поддеревьев у узла ограничена значениями -1, 0 или 1;

• после вставки и удаления возможна перестройка дерева;

• логарифмическая сложность операций гарантирована.

Обычное BST может работать быстро только при хорошем распределении данных. АВЛ-дерево обеспечивает скорость независимо от порядка вставок.

Баланс и высота

Высота узла — это длина пути от узла до самого глубокого листа в его поддереве. Баланс вычисляется как разница высот:

balance = height(left) − height(right)

Допустимые значения баланса в АВЛ-дереве:

• -1

• 0

• 1

Если баланс становится равен 2 или -2, узел считается несбалансированным. Требуется восстановление структуры.

Что такое балансировка

Балансировка — это операция перестройки связей между узлами, которая возвращает дереву допустимую разницу высот. Она выполняется через повороты.

Цель балансировки:

• уменьшить высоту перегруженной ветви;

• перераспределить узлы без нарушения правил BST;

• сохранить логарифмическую высоту дерева.

Балансировка запускается не по расписанию, а только при нарушении ограничения по высоте.

Повороты в АВЛ-дереве

Поворот — это локальное изменение связей между узлами. Он меняет структуру поддерева, но сохраняет упорядоченность значений.

Повороты бывают двух типов:

• простой поворот;

• двойной поворот.

Простой поворот затрагивает два узла. Двойной поворот затрагивает три узла и выполняется как два простых подряд.

Простой правый поворот

Правый поворот применяется при дисбалансе вида «лево-лево». Он уменьшает высоту левого поддерева.

Краткая логика:

• левый потомок становится новым корнем поддерева;

• исходный узел уходит вправо;

• правое поддерево левого потомка переносится влево к старому узлу.

Простой левый поворот

Левый поворот применяется при дисбалансе вида «право-право».

Краткая логика:

• правый потомок становится новым корнем поддерева;

• исходный узел уходит влево;

• левое поддерево правого потомка переносится вправо к старому узлу.

Двойные повороты

Двойные повороты нужны, когда простой поворот не исправляет ситуацию. Они встречаются при «ломаной» структуре ветвей.

Два варианта:

• левый-правый поворот (LR);

• правый-левый поворот (RL).

LR применяется, если узел перегружен влево, но его левый потомок перегружен вправо. RL — зеркальная ситуация.

Вставка узла

Вставка выполняется как в стандартном бинарном дереве поиска. Новый элемент размещается по ключу, проходом от корня вниз.

Порядок действий при вставке:

• сравнить ключ с текущим узлом;

• уйти влево, если ключ меньше;

• уйти вправо, если ключ больше или равен;

• вставить узел в позицию листа.

После вставки выполняется пересчет высот вверх по дереву. Затем проверяется баланс каждого узла на пути к корню. Если найден дисбаланс, выполняются повороты.

Особенности вставки в АВЛ-дереве:

• балансировка может сработать на нескольких уровнях;

• после поворота высоты пересчитываются заново;

• итоговая структура остается корректным BST.

Удаление узла

Удаление в АВЛ-дереве сложнее вставки. Сначала элемент удаляется по правилам BST, затем выполняется балансировка.

Основные случаи удаления:

• узел — лист: удаляется напрямую;

• у узла один потомок: узел заменяется потомком;

• у узла два потомка: выполняется замена на ближайший элемент по порядку.

Обычно используют минимальный узел из правого поддерева (in-order successor). Он гарантированно имеет не более одного потомка.

Алгоритм с заменой:

• найти удаляемый узел;

• найти минимальный элемент справа;

• заменить удаляемый узел найденным минимумом;

• восстановить связи поддеревьев;

• пересчитать высоты;

• выполнить балансировку.

После удаления баланс может нарушиться не только в одном месте. Балансировка часто идет вверх до корня, пока структура полностью не станет корректной.

Какие данные хранит узел

Узел АВЛ-дерева содержит ключ и ссылки на потомков. Также нужны данные для контроля высоты.

Минимальный набор полей:

• значение (ключ);

• ссылка на левого потомка;

• ссылка на правого потомка;

• высота узла или баланс-фактор.

Иногда вместо высоты хранят баланс. Но высота чаще удобнее, потому что баланс вычисляется по формуле.

Временная сложность операций

АВЛ-дерево сохраняет высоту порядка log(n), где n — число узлов. Это обеспечивает предсказуемое время работы.

Оценки по сложности:

• поиск: O(log n)

• вставка: O(log n)

• удаление: O(log n)

• обход дерева: O(n)

Балансировка добавляет небольшую постоянную нагрузку, но не меняет асимптотику.

Плюсы, ограничения

АВЛ-дерево дает стабильную производительность на любой последовательности данных. Это важно для систем, где нельзя допускать ухудшение скорости.

Преимущества:

• гарантированная логарифмическая высота;

• быстрый поиск, проверка наличия;

• устойчивость к вырождению;

• подходит для динамических данных с частыми изменениями.

Недостатки:

• сложнее реализация, чем у обычного BST;

• вставка и удаление требуют поворотов и пересчета высот;

• на практике может быть медленнее простых структур при малом объеме данных.

АВЛ-дерево выбирают, когда важна гарантия скорости и структура должна поддерживать упорядоченность в любой момент времени.

Где АВЛ-дерево особенно полезно

Структура эффективна в задачах, где нужно одновременно:

• поддерживать сортировку;

• выполнять много запросов поиска;

• часто вставлять, удалять элементы.

Примеры сценариев:

• хранение набора уникальных ключей;

• поддержка индексов в памяти;

• реализация ассоциативных контейнеров;

• проверка пересечений или существования значений.

АВЛ-дерево — это инструмент для работы с данными, который обеспечивает строгий баланс и стабильную скорость операций даже при неблагоприятном порядке изменений.

АВЛ-дерево - это структура данных, которая представляет собой бинарное дерево, обладающее следующими свойствами:

– Все листья дерева находятся на одной высоте. – Для каждого узла высота его левого поддерева отличается от высоты правого поддерева не более чем на 1. – Веса рёбер в АВЛ-дереве всегда различны.

АВЛ-деревья используются для хранения данных в упорядоченном виде и для быстрого поиска элементов. Они также применяются в алгоритмах сортировки и при решении задач на графы.