Числа Фибоначчи

Числа Фибоначчи — это последовательность целых чисел, в которой каждое последующее число равно сумме двух предыдущих:

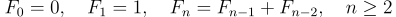
Эта простая формула породила одну из самых узнаваемых закономерностей в математике и науке. Последовательность используется в моделировании, теории чисел, информатике, визуализации данных и даже в криптографии.

Математические основы

Математические основы — это фундаментальная часть изучения чисел Фибоначчи. Здесь рассматриваются ключевые методы вычисления, аналитические формулы и теоретические закономерности. Понимание этих принципов позволяет использовать последовательность не только как математический объект, но и как инструмент анализа, моделирования и оптимизации в ИТ-задачах.

Формула Бине и ее вывод

Формула Бине выражает Fn в замкнутом виде:

Fn = (φⁿ − ψⁿ) / (φ − ψ)

где

φ = (1 + √5) / 2
ψ = (1 − √5) / 2

Эта запись получается из решения характеристического уравнения x² = x + 1. Решение приводит к двум корням — φ и ψ. Подставив их в общую форму линейной рекуррентной последовательности и применив начальные условия, получаем компактную формулу для любого n.

Формула Бине позволяет оценить порядок роста чисел без итераций и рекурсии, что особенно полезно в анализе алгоритмов и оценке вычислительной сложности.

Асимптотика роста

Рост последовательности Фибоначчи описывается приближением:

F(n) ≈ φⁿ / √5

где φ (фи) — золотое сечение, φ = (1 + √5) / 2 ≈ 1.61803.

Это выражение показывает, что последовательность растет экспоненциально: каждое следующее число примерно в 1.618 раза больше предыдущего. Уже при n = 10 значение F(n) = 55, а при n = 20 — 6765.

Во второй части формулы (ψⁿ / √5, где ψ = (1 − √5) / 2 ≈ −0.618) добавляется очень малая величина. Поскольку |ψ| < 1, её вклад быстро исчезает, и можно считать, что:

F(n) ≈ (1 / √5) × φⁿ

Ошибка такого приближения меньше 0.5 даже при малых n.

Отношение соседних членов стремится к золотому сечению:

F(n + 1) / F(n) → φ

Чем больше n, тем ближе отношение F(n + 1) / F(n) к постоянному пределу φ. Это делает золотое сечение естественным пределом последовательности и объясняет, почему оно так часто встречается в биологических, архитектурных и вычислительных системах.

Матричный способ вычисления

Последовательность Фибоначчи можно получить не только рекурсией, но и с помощью матричного возведения в степень. Если представить базовую рекуррентную зависимость в виде матрицы 2×2:

| 1  1 |
| 1  0 |

то при возведении её в степень n получается:

| 1  1 |ⁿ = | F(n+1)  F(n)   |
| 1  0 |  = | F(n)    F(n−1) |

Эта форма записи позволяет вычислять F(n) за логарифмическое время, то есть за O(log n). Метод основан на быстром возведении матрицы в степень и широко используется в вычислительных библиотеках.

Например, если n = 5:

| 1  1 |⁵ = | 8  5 |
| 1  0 |  = | 5  3 |

что соответствует значениям F(6) = 8, F(5) = 5 и F(4) = 3.

Числа Фибоначчи по модулю и период Пизано

Если рассматривать последовательность F(n) по модулю m, она становится периодической. Длина этого периода называется периодом Пизано и обозначается π(m).

Примеры:

π(2) = 3 → 0, 1, 1, 0, 1, 1, …
π(10) = 60 → 0, 1, 1, 2, 3, 5, 8, … (повтор через 60 элементов)
π(100) = 300

Периодичность по модулю важна в практических вычислениях — в генераторах случайных чисел, тестах на простоту и криптографии.

Свойства чисел Фибоначчи

1. Делимость: F(k) делит F(n) тогда и только тогда, когда k делит n.
2. Наибольший общий делитель: gcd(F(m), F(n)) = F(gcd(m, n)).
3. Четность: повторяется циклом длиной 3 — 0, 1, 1, 0, 1, 1, …
4. Фибоначчиевы простые: F(3)=2, F(4)=3, F(5)=5, F(11)=89, F(13)=233.

Обобщения и вариации

Последовательность Лукаса

L(0)=2, L(1)=1, L(n)=L(n−1)+L(n−2)

Связь с рядом Фибоначчи: L(n)=F(n−1)+F(n+1)

Трибоначчи, Тетрабоначчи и другие обобщения

T(n)=T(n−1)+T(n−2)+T(n−3)

Q(n)=Q(n−1)+Q(n−2)+Q(n−3)+Q(n−4)

X(n)=X(n−1)+X(n−2)+…+X(n−k)

Фибоначчиевы слова и квазипериодические последовательности

S(0)="0"

S(1)="01"

S(n)=S(n−1)+S(n−2)

Примеры: "0", "01", "010", "01001", "01001010", …

Числа Фибоначчи в алгоритмах и структурах данных

Фибоначчиева куча

• вставка и уменьшение ключа — O(1)
• извлечение минимума — O(log n)

Используется в алгоритмах Дейкстры и Прима.

Фибоначчи и динамическое программирование

F(0)=0, F(1)=1 для n≥2: F(n)=F(n−1)+F(n−2)

Пример: F(2)=1, F(3)=2, F(4)=3, F(5)=5

Разложение по Фибоначчи (код Зека)

Любое число N можно представить как сумму непоследовательных чисел Фибоначчи:

N = F(i₁) + F(i₂) + ... + F(iₖ)

Например: 100 = 89 + 8 + 3 = F(11) + F(6) + F(4)

Числа Фибоначчи и теория чисел

Диофантовы уравнения

x² − 5y² = ±4 Решения: x = F(2n+1), y = F(2n)

Фибоначчиевы простые

F(3)=2, F(5)=5, F(11)=89, F(23)=28657 Редкие и сложные для вычисления, применяются в тестах простоты и криптографии.

Фибоначчи и визуализация

Графические представления

• столбчатая диаграмма
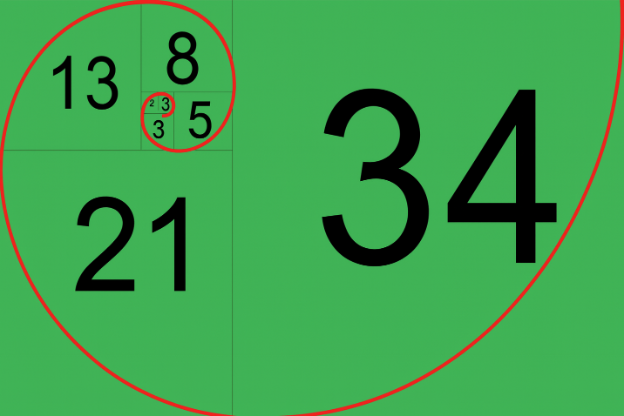
• спираль из квадратов со сторонами F(1), F(2), F(3), …
• фрактальные деревья

Золотая спираль

Последовательное построение квадратов с дугами, где стороны равны F(1), F(2), F(3), … Приближается к золотому сечению (φ ≈ 1.618).

Фракталы и визуальные паттерны

Используются в распределении точек, 3D-графике и архитектуре.

Современные технологические применения

Криптография и генераторы случайных чисел

Xₙ = (Xₙ₋ₚ + Xₙ₋ₛ) mod m

Применяется в криптографии и моделировании.

Машинное обучение и оптимизация

Фибоначчиев поиск используется для нахождения минимума функции одной переменной.

Сжатие данных и кодирование

Фибоначчиев код (код Зека) обеспечивает компактное и однозначное кодирование.

Блокчейн и генерация ключей

Применяются фибоначчиевы рекуррентные схемы для генерации ключей с нелинейной структурой.

Фибоначчи в культуре и философии

Числа Фибоначчи встречаются:

• в кино («Пи», «Код да Винчи»),
• в архитектуре (Палладио, Ле Корбюзье),
• в дизайне и интерфейсах.

Поп-культура и псевдонаука

Популярные источники придают золотому сечению излишнюю универсальность, хотя в природе формы лишь приближенно ему соответствуют.

Математика Фибоначчи остается мощным инструментом анализа, но не универсальным законом мироздания.

Числа Фибоначчи (или последовательность Фибоначчи) - это такая бесконечная числовая последовательность, в которой первые два числа равны 0 и 1, а далее, начиная с третьего, каждое число равно сумме двух предыдущих:

То есть, мы видим, что:

и так далее.