Линейная регрессия

Линейная регрессия — это математическая модель, описывающая зависимость одной количественной переменной от одной или нескольких других переменных с помощью линейной функции. Метод относится к статистическому анализу, применяется для прогнозирования и анализа данных, используется в аналитике, экономике, инженерии и машинном обучении.

Назначение

Линейная регрессия решает задачу предсказания числового значения целевой переменной на основе известных признаков. Цель — выявить и формализовать связь между входными данными и результатом в виде уравнения.

Основные задачи:

• прогнозирование значений;

• анализ влияния факторов;

• выявление закономерностей в данных;

• аппроксимация зависимостей.

В машинном обучении регрессия относится к задачам обучения с учителем, где известны входные данные и правильные ответы.

Формальная постановка задачи

Задача линейной регрессии заключается в предсказании переменной Y на основе набора признаков X. Каждое наблюдение описывается набором параметров, а модель подбирает такие коэффициенты, при которых ошибка прогноза минимальна.

Если используется один признак, модель называется простой линейной регрессией. При использовании нескольких признаков — множественной.

Простая линейная регрессия

Описывается уравнением:

f(x) = b + m·x

где:

• x — независимая переменная;

• m — коэффициент наклона;

• b — свободный член;

• f(x) — прогнозируемое значение.

Коэффициент m определяет, как сильно изменяется результат при изменении признака. Коэффициент b задает смещение линии относительно оси значений.

Изменение параметров влияет на модель следующим образом:

• увеличение m усиливает наклон линии;

• изменение b сдвигает линию вверх или вниз.

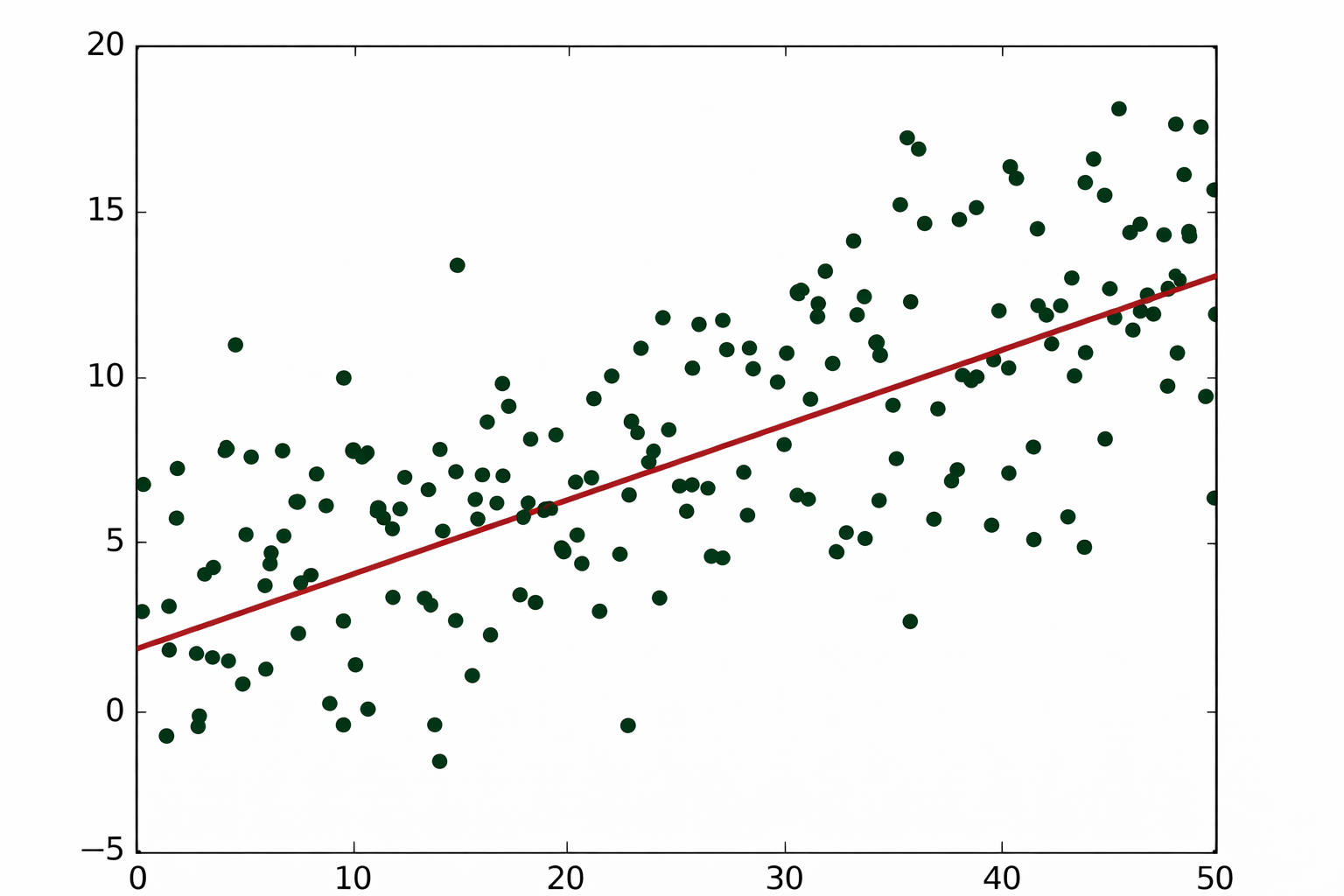
Геометрическая интерпретация

При визуализации данных линейная регрессия представляется в виде прямой линии, проведенной через множество точек. Идеальное совпадение невозможно, если данные содержат шум или неравномерно распределены. Задача модели — найти такое положение прямой, при котором суммарное отклонение точек от нее минимально. Эти отклонения называются остатками.

Функция потерь

Для оценки качества модели используется функция потерь. Она измеряет, насколько сильно прогнозируемые значения отличаются от реальных.

Наиболее распространенная функция потерь — среднеквадратичная ошибка (MSE):

• вычисляет квадрат разницы между прогнозом и фактическим значением;

• суммирует ошибки по всем наблюдениям;

• усредняет результат.

Чем меньше значение MSE, тем точнее модель описывает данные.

Оптимизация модели

Коэффициенты регрессии подбираются таким образом, чтобы минимизировать функцию потерь. Для этого используются аналитические методы или численные алгоритмы оптимизации.

Процесс оптимизации включает:

• инициализацию коэффициентов;

• вычисление ошибки;

• корректировку параметров;

• повторение шагов до сходимости.

Результатом является набор коэффициентов, обеспечивающий наилучшее приближение.

Применение в анализе данных

Типичные примеры:

• зависимость цены недвижимости от площади;

• связь выручки с объемом инвестиций;

• прогноз спроса по историческим данным;

• оценка влияния параметров на результат.

Модель позволяет не только прогнозировать значения, но и интерпретировать вклад каждого фактора.

Реализация в Python

Для построения регрессии используются стандартные библиотеки анализа данных. Типовой процесс включает:

• загрузку данных;

• выбор признаков и целевой переменной;

• обучение модели;

• оценку качества;

• визуализацию результатов.

Чаще всего применяются:

• pandas для работы с таблицами;

• matplotlib для графиков;

• scikit-learn для реализации модели.

Модель обучается на исторических данных и затем используется для прогнозов.

Множественная линейная регрессия

В реальных задачах результат зависит от нескольких факторов. В этом случае используется множественная линейная регрессия.

Общее уравнение имеет вид:

f(x) = b + m₁·x₁ + m₂·x₂ + … + mₙ·xₙ, где каждый коэффициент соответствует отдельному признаку.

Особенности:

• учитывает вклад каждого параметра;

• позволяет анализировать значимость признаков;

• чувствительна к корреляции между переменными.

Интерпретация коэффициентов позволяет понять, какие факторы оказывают наибольшее влияние.

Ограничения метода

Линейная регрессия эффективна не во всех случаях. Метод имеет ряд ограничений:

• предполагает линейную зависимость;

• чувствителен к выбросам;

• плохо работает с нелинейными процессами;

• требует нормального распределения ошибок.

При нарушении предположений точность модели снижается.

Линейная регрессия - это метод статистического анализа, который используется для предсказания значения зависимой переменной на основе одной или нескольких независимых переменных. Линейная регрессия строится на предположении, что между зависимой и независимыми переменными существует линейная связь.