Вектор

Вектор — это математический объект, задающий одновременно величину и направление. В отличие от скалярной величины, у которой есть только одно числовое значение, вектор описывает ориентированную «стрелку» в пространстве и задается набором координат. В математике вектором представляют скорость, ускорение, силу, перемещение. В информатике вектор понимают как упорядоченный набор чисел, который можно хранить в памяти и обрабатывать алгоритмами.

Свойства и характеристики векторов

Вектор в линейной алгебре — элемент векторного пространства. Для него определены операции сложения и умножения на число, а также длина и направление. В прикладных задачах важны способы задания вектора и интерпретация его компонент.

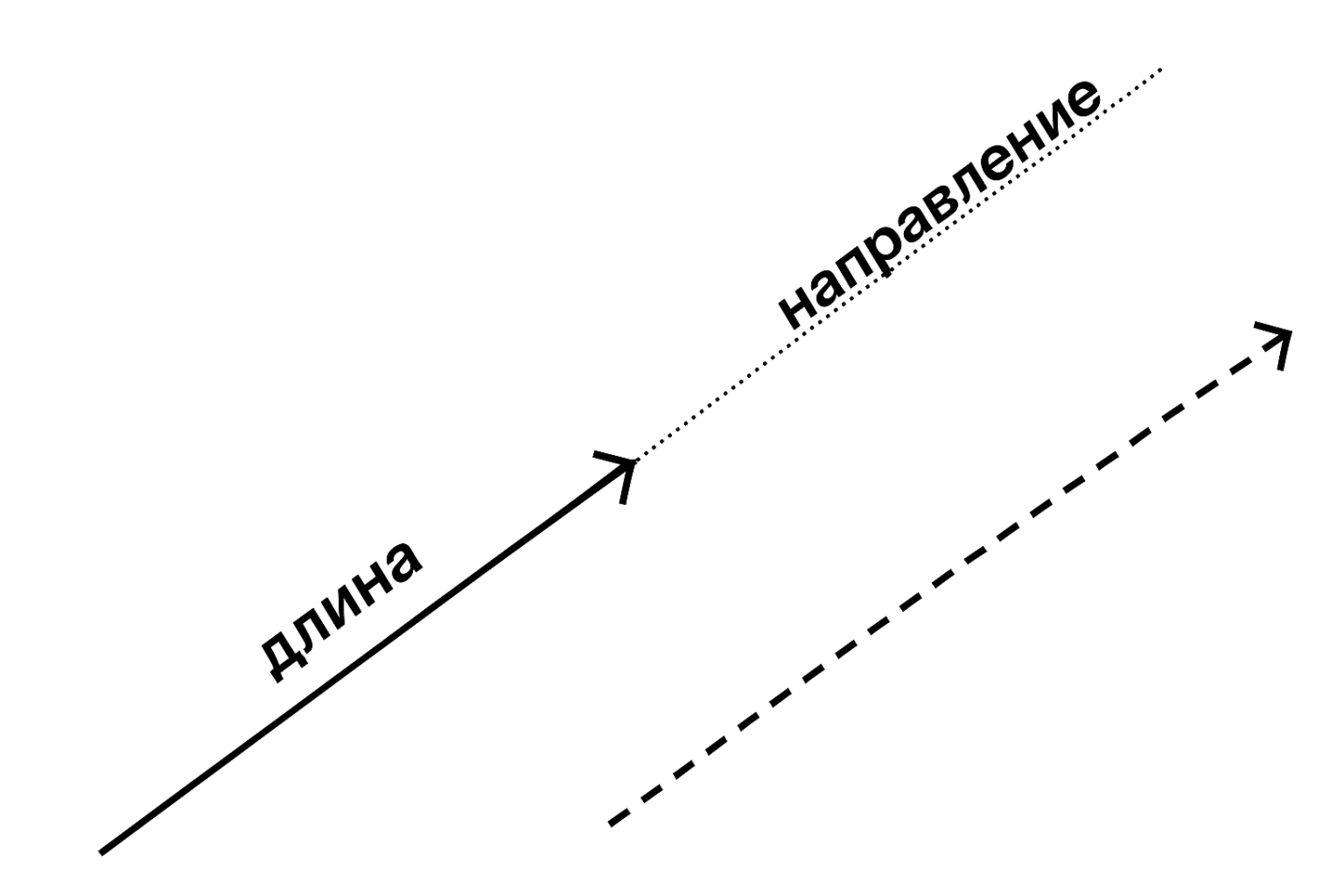
Длина и направление

Длину вектора называют модулем. Для вектора в декартовой системе координат длина вычисляется как корень из суммы квадратов компонент. Направление задается точкой, в которую «смотрит» стрелка, или нормированным вектором единичной длины. В задачах навигации длина соответствует, например, пройденному пути, а направление — курсу движения.

Способы задания векторов

Вектор можно задать несколькими способами:

• набором координат в выбранной системе;

• точками начала и конца, из которых координаты выводятся;

• длиной и направлением относительно базисных осей;

• как строку или столбец чисел в виде матрицы.

В вычислительной технике чаще используют представление вектора как массива чисел фиксированной или переменной длины. Тип компонент зависит от задачи: целые числа, вещественные, комплексные значения.

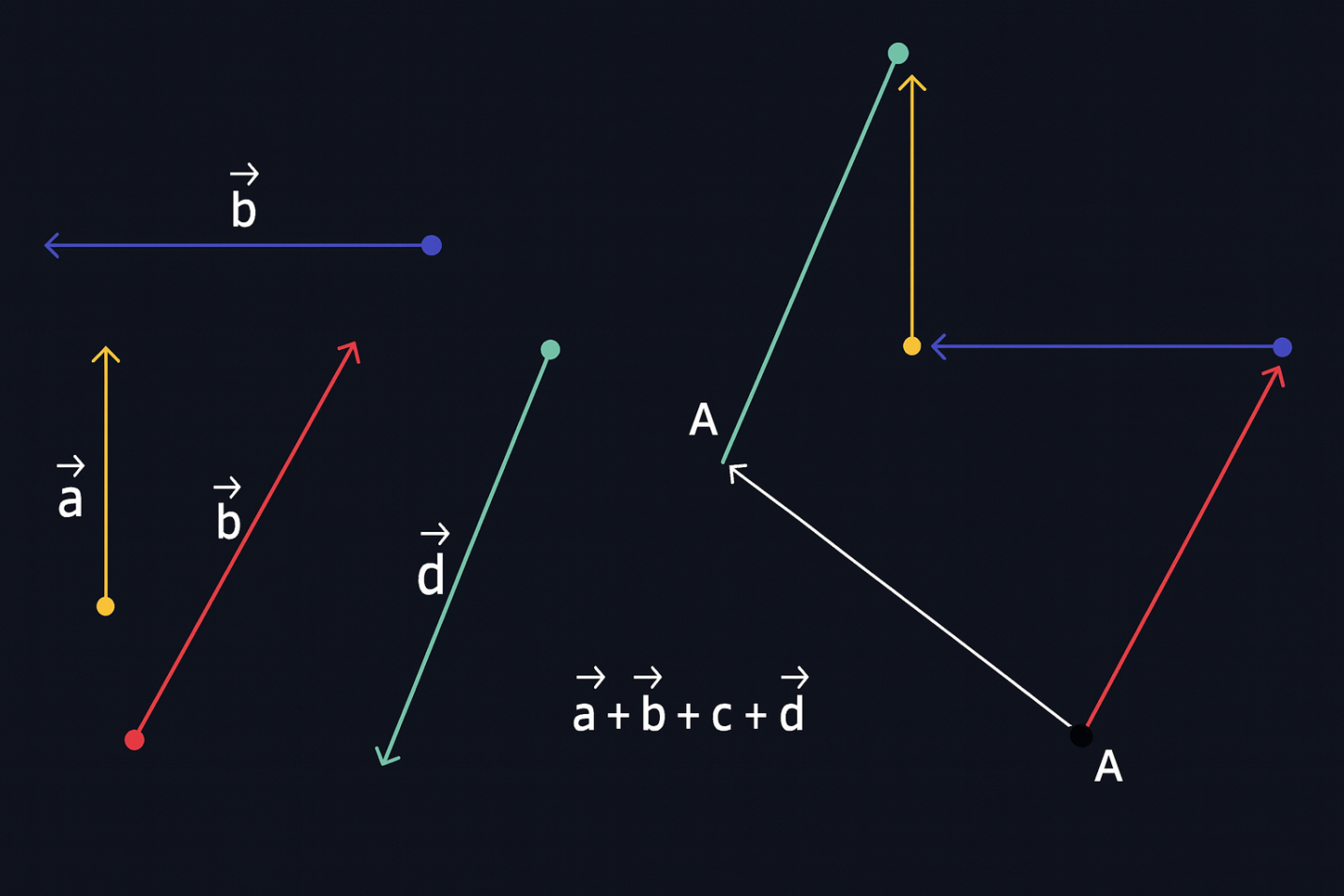
Операции над векторами

Над векторами выполняют алгебраические и геометрические операции. Они лежат в основе вычислительной геометрии, компьютерной графики, физического моделирования.

Базовые алгебраические операции

К ключевым операциям относятся:

• сложение векторов — поэлементное суммирование компонент;

• вычитание — поэлементная разность компонент;

• умножение вектора на число — масштабирование длины без изменения направления;

• покомпонентное умножение — используется в отдельных алгоритмах обработки сигналов и изображений.

Результат каждой операции также является вектором и может участвовать в дальнейших вычислениях.

Скалярное и векторное произведение

Скалярное произведение двух векторов возвращает число. Оно равно произведению их длин и косинуса угла между ними. В координатной форме это сумма произведений соответствующих компонент. Скалярное произведение применяют для:

• вычисления угла между направлениями;

• проверки ортогональности;

• оценки близости объектов в задачах поиска и рекомендаций;

• вычисления работы силы в физике.

Векторное произведение определено для трехмерных векторов. Результат — новый вектор, перпендикулярный плоскости исходных. Его длина пропорциональна площади параллелограмма, построенного на исходных векторах. Операция используется при вычислении нормалей к поверхностям, момента сил, ориентации объектов в 3D. В графических движках векторное произведение применяют при расчете освещения и обработке столкновений.

Применение векторов в программировании

Вектор в программировании — удобная структура данных для хранения последовательностей чисел, параметров или ссылок на объекты.

Структуры данных и массивы

Во многих языках термин «вектор» соответствует динамическому массиву. Такая структура:

• хранит упорядоченный набор элементов;

• позволяет обращаться к элементу по индексу за константное время;

• поддерживает операции вставки и удаления;

• может автоматически расширять внутренний буфер.

На уровне алгоритмов такой вектор интерпретируют как точку в многомерном пространстве признаков или как набор параметров модели. Для высокопроизводительных систем важны локальность доступа к памяти и компактное хранение компонент, поэтому векторы часто реализуются как непрерывные участки памяти без разрывов.

Графика и физические симуляции

В компьютерной графике векторами представляют:

• положение точек и вершин;

• направление и интенсивность освещения;

• нормали к поверхностям;

• скорости и ускорения объектов;

• ориентацию камер и источников света.

В физических движках вектора описывают силы, импульсы, перемещения. Численный интегратор шаг за шагом обновляет вектор состояния системы: координаты, скорости, ориентации. Это позволяет воспроизводить реалистичное движение тел и взаимодействие объектов в реальном времени. Точность таких симуляций зависит от корректной реализации операций над векторами и выбора шага интегрирования.

Векторы в задачах анализа данных

В анализе данных вектор — базовое представление объекта. Каждому объекту сопоставляется набор признаков, и этот набор записывается как вектор в пространстве признаков. Все последующие операции машинного обучения и статистики работают именно с такими векторами.

Векторные представления в машинном обучении

Примеры векторного представления:

• пользователь онлайн-сервиса описывается вектором из чисел, отражающих активность и интересы;

• текст переводится в вектор через мешок слов, TF-IDF или распределенные представления;

• изображение кодируется вектором признаков, извлеченных нейронной сетью;

• временной ряд представляется как вектор значений в скользящем окне.

На векторах выполняются:

• нормализация и стандартизация;

• вычисление расстояний и метрик близости;

• проекции на подпространства и понижение размерности;

• кластеризация и классификация;

• обучение регрессионных и нейросетевых моделей.

Качество векторного представления напрямую влияет на точность моделей.

Рекомендательные системы и поиск

Векторные представления лежат в основе современных рекомендательных систем. Система строит векторы пользователей и объектов, затем сравнивает их по косинусному расстоянию или другим метрикам. Близкие векторы интерпретируются как похожие интересы или свойства. Такой подход применяется:

• в рекомендациях товаров и контента;

• в персонализированных новостных лентах;

• в поиске по семантической близости текстов и изображений;

• в задачах ранжирования и таргетинга рекламы.

В системах поиска векторные индексы позволяют выполнять запросы по смыслу, а не только по точному совпадению слов. Для этого используют структуры данных, оптимизированные под хранение и сравнение больших наборов векторных представлений.

Графическая визуализация векторов

Визуализация помогает контролировать корректность вычислений и анализировать поведение моделей. Для векторов используют двумерные и трехмерные графики, поля стрелок, диаграммы.

Подходы к визуализации

Основные варианты представления:

• отдельные векторы на координатной плоскости или в пространстве;

• поля векторов для отображения распределений скоростей и сил;

• траектории, построенные по последовательности векторов;

• тепловые карты, отображающие величины компонентов;

• анимации, показывающие изменение векторных величин во времени.

В простых случаях достаточно библиотек построения графиков, которые умеют рисовать стрелки и поверхности. Для сложных сцен применяются графические движки и специализированные инструменты визуализации научных данных.

Ресурсы для практического освоения

Для работы с векторами в ИТ важно сочетать теорию и практику. Требуется базовая математическая подготовка и навыки программирования.

Литература, IDE и библиотеки

Пригодятся следующие типы ресурсов:

• учебники по линейной алгебре и аналитической геометрии;

• книги по численным методам и компьютерной графике;

• документация языков программирования и стандартных библиотек;

• справочные материалы по статистике и машинному обучению.

Для практических экспериментов используют:

• интегрированные среды разработки с поддержкой отладки численных вычислений;

• библиотеки линейной алгебры и работы с массивами;

• инструменты визуализации графиков и 3D-сцен;

• тестовые проекты, в которых реализованы базовые операции с векторами и простые модели.

Освоение векторов как математического и программного объекта упрощает проектирование ИТ-систем, повышает качество моделей и делает работу с данными более предсказуемой и контролируемой.

Вектор - это математический объект, который имеет величину и направление. Он может быть использован для описания скорости, ускорения, силы и других физических величин. Векторы можно складывать, вычитать, умножать на числа и на другие векторы, а также скалярно умножать.

Вектор может означать направление развития компании или продукта, стратегию продвижения, план действий для достижения цели. Также вектором может называться последовательность шагов, которые нужно выполнить для достижения определенной цели или решения задачи.