Корреляция

Корреляция — это статистическая мера, показывающая степень связи между двумя или более переменными. Она описывает, насколько согласованно изменяются величины: если рост одной сопровождается ростом другой, связь положительная; если одна увеличивается, а вторая уменьшается — отрицательная. Отсутствие корреляции означает, что изменения одной переменной не сопровождаются предсказуемыми изменениями другой. В отличие от зависимости, корреляция не утверждает причинно-следственную связь: совпадение в динамике может быть результатом влияния третьего фактора или просто случайным пересечением данных.

В повседневной жизни корреляцию можно заметить в самых разных контекстах. Продажи мороженого растут летом вместе с количеством пожаров — не потому, что одно вызывает другое, а потому что обе величины связаны с температурой. Аналогично, повышение конверсии и рост рекламного бюджета могут совпадать во времени, но истинная причина может лежать в сезонном интересе к продукту.

Виды и формы корреляции

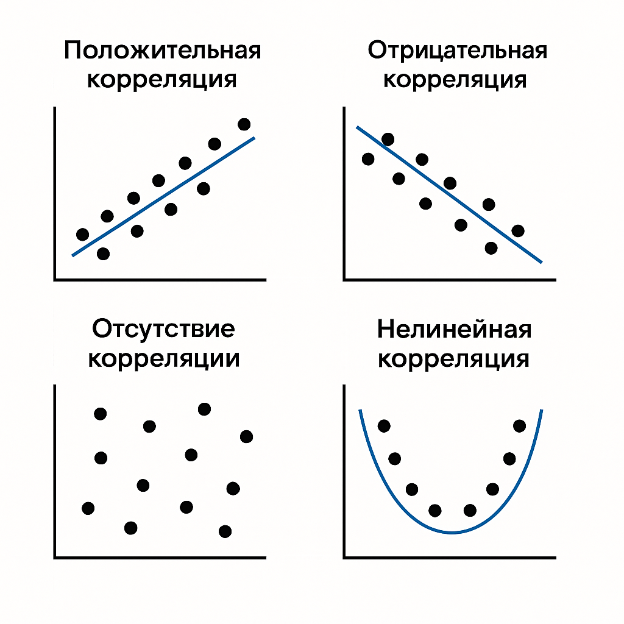
Корреляция бывает разной по направлению и характеру зависимости между переменными. Прежде всего различают положительную, отрицательную и нулевую корреляцию — в зависимости от того, как изменяются значения относительно друг друга.

• Положительная корреляция означает, что увеличение одной переменной сопровождается увеличением другой. Чем выше значение первой, тем выше в среднем значение второй. Такой тип связи наблюдается, например, между временем обучения и результатами тестов: больше часов подготовки — выше оценка.

• Отрицательная корреляция отражает обратную зависимость: при росте одной переменной другая уменьшается. Примером может служить связь между пробегом автомобиля и его остаточной стоимостью — чем больше пробег, тем ниже цена.

• Отсутствие корреляции (нулевая корреляция) фиксируется, когда изменения одной переменной не оказывают систематического влияния на другую. Например, рост количества выпитого кофе не влияет на результаты лотерейных розыгрышей — переменные независимы.

По форме зависимости различают линейную и нелинейную корреляцию.

• Линейная связь проявляется, когда зависимость между переменными можно описать прямой линией. На диаграмме рассеяния точки располагаются вдоль наклонной оси: чем плотнее они группируются вокруг линии, тем выше коэффициент корреляции по модулю. Например, при прямом увеличении цены и спроса на ограниченный товар наблюдается линейная положительная корреляция.

• Нелинейная корреляция возникает, если зависимость имеет более сложную форму — кривую, параболу или другую нелинейную траекторию. При такой связи коэффициент Пирсона может показывать слабое или нулевое значение, хотя зависимость очевидна визуально. Типичный пример — зависимость продуктивности от уровня стресса: при низком стрессе эффективность растет, затем достигает пика, а при чрезмерной нагрузке снова падает. График в этом случае напоминает перевернутую букву U.

Математическая суть

Чаще всего для количественной оценки используется коэффициент корреляции Пирсона. Он вычисляется по формуле:

r = cov(X, Y) / (σX * σY)

где cov(X, Y) — ковариация переменных X и Y, а σX и σY — их стандартные отклонения. Ковариация отражает направление совместных изменений, стандартное отклонение характеризует разброс значений. Коэффициент r принимает значения от −1 до 1. Чем ближе r к 1, тем сильнее положительная связь; чем ближе к −1 — тем сильнее отрицательная; около нуля — зависимость отсутствует или носит нелинейный характер.

Простой пример: если X = [1, 2, 3], а Y = [2, 4, 6], то коэффициент r ≈ 1, что указывает на почти идеальную прямую связь. При Y = [6, 4, 2] значение r ≈ −1 — сильная обратная зависимость. Если r близко к нулю, линейной связи нет, хотя переменные все же могут быть связаны сложнее, чем линейно.

Интерпретация значений

Корреляция не только вычисляется, но и интерпретируется с учетом контекста. Принято считать, что |r| < 0.3 означает слабую связь, 0.3–0.7 — умеренную, а значения выше 0.7 — сильную. Однако строгих границ нет: сила корреляции зависит от объема выборки и природы данных.

Нулевое значение не гарантирует отсутствие связи. Например, если зависимость между переменными имеет форму параболы, линейный коэффициент Пирсона даст r ≈ 0, хотя взаимосвязь очевидна визуально. Выбросы также искажают оценку: одна экстремальная точка способна радикально изменить величину коэффициента. Поэтому интерпретация всегда требует проверки распределения данных и визуального анализа диаграммы рассеяния.

Корреляция и причинность

Одно из ключевых заблуждений — считать корреляцию доказательством причинности. Даже сильная статистическая связь не означает, что изменение одной переменной вызывает изменение другой. Влияние может оказывать третья, скрытая переменная — confounding variable. Классический пример: рост числа утоплений и увеличение продаж мороженого совпадают из-за жары, а не из-за прямой зависимости.

Такие ложные совпадения называют spurious correlation — мнимыми корреляциями. Они могут возникать при большом числе наблюдений и разнообразии факторов. Поэтому профессиональный анализ всегда предполагает проверку гипотез и построение моделей, которые подтверждают или опровергают наличие причинно-следственной связи.

Коэффициенты корреляции

Разные типы данных требуют разных способов измерения связи. Универсального коэффициента не существует: выбор зависит от природы переменных — количественных, ранговых или категориальных.

Классические коэффициенты

• Коэффициент Пирсона (r) используется для количественных данных, имеющих нормальное распределение. Он измеряет силу и направление линейной связи между двумя переменными. Значение r варьируется от −1 до 1, где крайние значения указывают на идеальную прямую зависимость, а ноль — на отсутствие линейной связи.
• Коэффициент Спирмена (ρ) применяют для ранговых данных, где значения можно упорядочить, но интервалы между ними неравномерны. Он основан на корреляции рангов, устойчив к выбросам и подходит, если распределение данных не является нормальным.
• Коэффициент Кендалла (τ) также оценивает связь между ранговыми или порядковыми переменными. Он учитывает количество согласованных и несогласованных пар наблюдений. Этот метод более консервативен, чем Спирмена, и используется для небольших выборок.

Специальные коэффициенты

• Фи-корреляция (φ) применяется для бинарных переменных — когда данные представлены в виде «да/нет», «0/1». Она измеряет степень связи между двумя дихотомическими признаками.
• Коэффициент Крамера (V) используется для номинальных переменных, не имеющих порядка (например, тип продукта, категория клиента). Он основан на статистике χ² и показывает силу связи между категориальными признаками.
• Корреляционное отношение (η) оценивает степень нелинейной зависимости между переменными. Оно измеряет, насколько вариация одной переменной объясняется изменением другой, не предполагая линейной формы.

Выбор коэффициента по типу данных

Проверка значимости

Корреляция, рассчитанная по выборке, может быть результатом случайности. Чтобы подтвердить ее достоверность, применяют статистическую проверку гипотез.

Нулевая гипотеза формулируется как H₀: r = 0 — между переменными нет связи. Альтернативная гипотеза H₁ утверждает, что связь существует. Для оценки используют p-value: если p < 0.05, корреляция считается статистически значимой.

Размер выборки напрямую влияет на надежность результата. При малом объеме даже сильная корреляция может оказаться ложной, а при большой выборке — наоборот, незначительные зависимости могут оказаться статистически значимыми.

Дополнительно используют доверительные интервалы, которые показывают диапазон возможных значений истинного коэффициента. Чем уже интервал, тем стабильнее оценка.

Визуализация корреляции

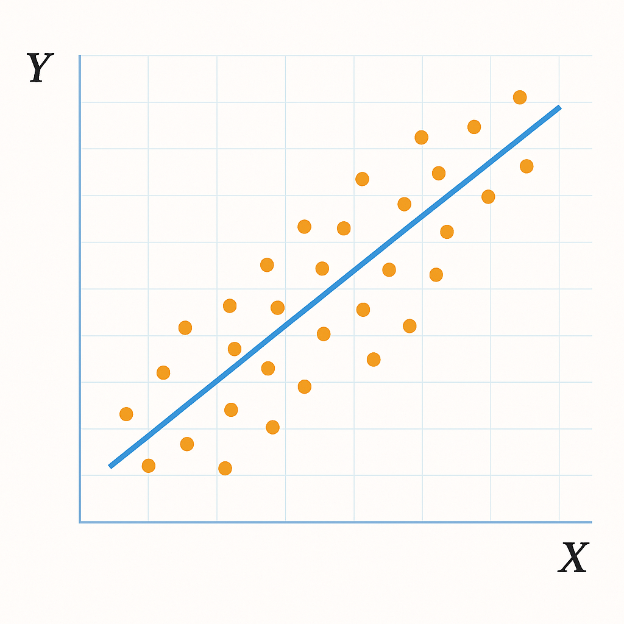
Корреляцию удобно представлять графически. Наиболее распространенный способ — диаграмма рассеяния. Каждая точка отображает пару значений, а направление облака точек указывает на характер зависимости. Если точки выстраиваются вдоль восходящей линии, связь положительная; если вдоль нисходящей — отрицательная.

Добавление линии регрессии помогает визуализировать общий тренд и оценить, насколько данные близки к линейной зависимости. При сильной корреляции линия хорошо описывает данные, при слабой — точки распределены шире.

Для множественных переменных применяют тепловые карты — матрицы корреляций. Каждая ячейка показывает значение коэффициента между парами переменных, а цвет передает направление и силу связи. Тепловые карты позволяют быстро выявить взаимозависимые признаки в больших массивах данных, что особенно полезно при анализе фичей в машинном обучении.

Где используется корреляция

Корреляционный анализ является универсальным инструментом и применяется в разных областях.

• В статистике и научных исследованиях он помогает выявлять взаимосвязи между показателями, формулировать гипотезы и подтверждать закономерности.
• В машинном обучении корреляция используется при фичевой инженерии — для отбора и фильтрации признаков. Высокая взаимная корреляция между фичами указывает на избыточность данных, которую нужно устранить для повышения устойчивости модели.
• В бизнес-аналитике корреляция помогает понять, какие факторы влияют на доход, спрос или удержание клиентов. Аналитики оценивают связь между маркетинговыми активностями, временем отклика, конверсией и другими показателями.
• В маркетинге метод используется для анализа поведения потребителей: например, насколько рост кликов по рекламе связан с количеством покупок.
• В журналистике данных корреляция помогает находить скрытые взаимосвязи между социальными и экономическими явлениями, визуализировать их и представлять в наглядной форме.

Инструменты и способы расчета

Корреляцию можно вычислить вручную, в электронных таблицах или с помощью языков программирования.

При ручных расчетах используют формулу коэффициента Пирсона:

r = cov(X, Y) / (σX * σY)

Метод подходит для обучения, но не для больших выборок.

В Excel и Google Sheets встроена функция CORREL, которая возвращает коэффициент Пирсона. Для визуализации доступны диаграммы рассеяния и линейные тренды.

В Python анализ проводят с помощью библиотек numpy (функция corrcoef), pandas (метод DataFrame.corr) и seaborn, который строит тепловые карты корреляционных матриц.

В R используются функции cor() и corrplot(), обеспечивающие широкий спектр визуализаций и методов оценки. Онлайн-калькуляторы подходят для учебных задач и быстрой проверки, но не дают возможности автоматизировать анализ.

Выбор инструмента зависит от задачи: для научных расчетов предпочтителен R, для аналитики и ИТ — Python, для офисной работы — электронные таблицы.

Ошибки и подводные камни

Анализ корреляции требует осторожности. Частые ошибки включают:

• малый объем выборки, при котором результаты нестабильны;
• выбросы, способные исказить значение коэффициента;
• мультиколлинеарность, когда переменные сильно коррелируют между собой, что нарушает интерпретацию регрессионных моделей;
• неверный выбор коэффициента для типа данных;
• ошибочную интерпретацию корреляции как причины.

Для надежного анализа необходимо проверять качество данных, использовать визуализацию и подтверждать выводы дополнительными статистическими тестами.

История и происхождение

Термин «корреляция» предложил Фрэнсис Гальтон в конце XIX века при изучении наследственных признаков. Он впервые заметил, что статистические зависимости между ростом родителей и детей можно выразить количественно.

Карл Пирсон, развивая идеи Гальтона, предложил формулу коэффициента корреляции и создал математический аппарат, который стал основой современной статистики. С тех пор корреляционный анализ используется во всех научных дисциплинах, от биологии до машинного обучения.

Использовать корреляцию следует тогда, когда требуется измерить степень связи и оценить направление влияния, но окончательные выводы нужно подтверждать экспериментами или моделированием. В современной аналитике, экономике и ИТ-контексте корреляционный анализ — ключ к интерпретации сложных систем и принятию обоснованных решений.