Основы статистического распределения — Математика для аналитиков

• Распределение
• Нормальное распределение
• Равномерное распределение
• Биномиальное распределение
• Доверительный интервал
• Нормальное и t-распределение
• Центральная предельная теорема
• Выводы

В этом уроке мы изучим распределение. Этот инструмент помогает построить график и с его помощью посмотреть на все значения, которые принимает изучаемая величина. Таким образом мы можем понять, какие значения в целом принимает переменная. График с распределением помогает идентифицировать выбросы, и в итоге оценивать точность прогнозов.

Также мы изучим центральную предельную теорему, которая помогает создавать более точные и надежные алгоритмы кластеризации и классификации данных. Например, с ее помощью мы можем изучить свойства котиков в нашей лаборатории и сделать выводы обо всех котиках на Земле.

Распределение

Распределение данных – это таблица, которая показывает, какова вероятность встретить то или иное значение переменной X. Еще такая таблица называется «рядом распределения» или «законом дискретной случайной величины».

Также распределение можно представить в виде графика или математической модели. Его можно построить в таблице, в Excel, с помощью Python и многими другими способами. Подробнее об этом можно почитать, перейдя по ссылкам в конце урока.

Есть множество разных типов распределений данных, вот самые распространенные:

1. Нормальное распределение
2. Равномерное распределение
3. Биномиальное распределение
4. Геометрическое распределение
5. Распределение Пуассона

В этом уроке мы поговорим о первых трех типах распределения.

Нормальное распределение

Нормальное распределение имеет такие особенности:

• График имеет форму колокола
• Среднее и медиана равны и расположены в центре распределения
• Около 68% данных находятся в пределах одного стандартного отклонения от среднего
• Около 95% данных находятся в пределах двух стандартных отклонений от среднего
• Около 99,7% данных находятся в пределах трех стандартных отклонений от среднего значения

Последние три пункта известны как эмпирическое правило (правило 68-95-99,7).

Для примера рассмотрим такую задачу:

Рост мальчиков распределен нормально со средним значением μ = 70 дюймов и стандартным отклонением σ = 2 дюйма. Какой процент мальчиков в этой школе выше 74 дюймов?

По этому условию мы можем сделать такие выводы:

• Среднее значение 70 дюймов находится посередине
• Каждое стандартное отклонение равно расстоянию в 2 дюйма
• Рост в 74 дюйма на два стандартных отклонения выше среднего: 2.2%

Нарисуем кривую с нормальным распределением данных из этой задачи:

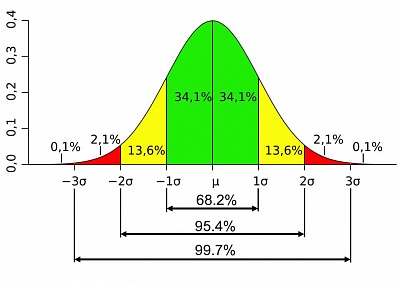
На практике, правильно использовать калькулятор или таблицу нормального распределения для решения подобных задач.

Решим эту задачу с помощью таблицы нормального распределения. В таблице распределения указаны значения вероятности, площади под кривой для разных значений стандартного отклонения. По вертикали указаны целые и десятые значения для величины отклонения, а по горизонтали - сотые.

Найдем в таблице значение для двух отклонений, z = 2, и увидим, что это .0228.

Равномерное распределение

Равномерное распределение — это такое распределение вероятностей, при котором каждое значение в интервале от a до b равновероятно. Например, у шестигранного кубика вероятность выпадения любой грани всегда одинакова — это 1/6.

Для примера представим, что случайная величина X подчиняется равномерному распределению. Нам нужно найти вероятность того, что X примет значение между x₁ и x₂. Чтобы это сделать, воспользуемся такой формулой:

P(x₁ < X < x₂) = (x₂ - x₁) / (b - a)

В формуле выше:

• x₁ — меньшее процентное значение
• x₂ — верхнее процентное значение
• a — минимально возможное значение
• b — максимально возможное значение

Так будет выглядеть график:

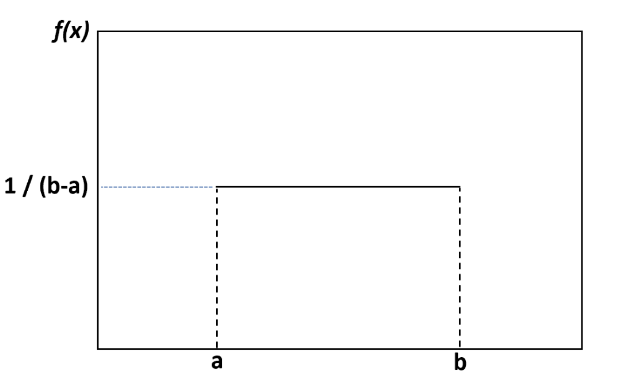
Перечислим свойства равномерного распределения:

• Среднее значение (математическое ожидание): μ = (a + b) / 2
• Дисперсия: σ ^2=(b - a)^2/12
• Стандартное отклонение: σ = (b-a)/√(12)
• Равномерное распределение не имеет моды

Биномиальное распределение

Биноминальным распределением описывается вероятность достижения k успехов в n биномиальных экспериментах. Представим, что мы подбрасываем монету пять раз. Здесь количество появлений орла — это случайная величина X, распределенная по биномиальному закону. Орел обязательно выпадет какое-то количество раз:

• x₀ = 0 раз
• или x₁ = 1 раз
• или x₂ = 2 раза
• или x₃ = 3 раза
• или x₄ = 4 раза
• или x₅ = 5 раз

Соответствующие вероятности определяются формулой Бернулли. На следующей диаграмме показано распределение вероятностей при n = 200 и p = 0,5:

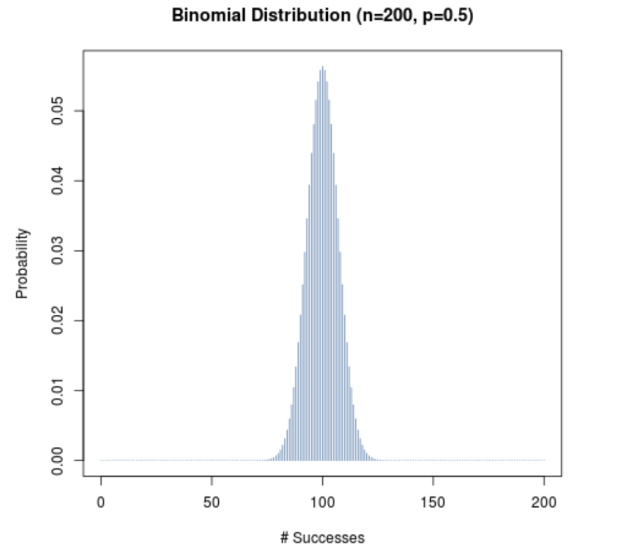
Доверительный интервал

Доверительный интервал выражает диапазон значений, в котором с определенной вероятностью находится истинное значение параметра генеральной совокупности. Например, если мы хотим оценить средний рост всех людей в генеральной совокупности, мы можем провести исследование на выборке из 1000 человек и получить средний рост 170 см в этой выборке. В таком случае доверительный интервал может быть равен 165-175 см. Другими словами, с вероятностью 95% истинное среднее значение лежит в этом диапазоне.

Чтобы посчитать доверительный интервал, нужно:

• Определить выборочную среднюю x̄ и стандартное отклонение (s) для этой выборки
• Выбрать нужный уровень доверия (обычно используют 95% или 99%)
• Найти стандартную ошибку среднего — поделить стандартное отклонение (s) на квадратный корень из числа наблюдений (n)
• Найти границы доверительного интервала по формуле x+-(значение t-распределения со степенью свободы n-1 и уровнем доверия α/2) * (стандартная ошибка среднего)

Нормальное и t-распределение

Нормальное распределение используется на практике чаще всего, но нередко его нужно заменить на t-распределение. Мы используем критические значения из таблицы t вместо таблицы z, когда выполняется одно из следующих условий:

• Мы не знаем стандартного отклонения случайной величины
• Размер выборки меньше или равен 30

Центральная предельная теорема

Центральная предельная теорема (ЦПТ) утверждает, что сумма большого числа случайных независимых величин приближается к нормальному распределению. Если взять большую выборку из исходных данных, рассчитать ее среднее значение и построить распределение ее средних значений, то оно будет приближаться к нормальному. При этом не важно, были ли исходные данные нормально распределенными.

ЦПТ играет важную роль в статистике, потому что она помогает выяснить, насколько точным будет среднее значение выборки для оценки всей генеральной совокупности.

Допустим, мы собрали данные о росте всех жителей города и хотим узнать их средний рост. Можно не использовать весь набор данных, а взять из него случайную выборку из 100 человек и вычислить их средний рост. Этот процесс можно повторить много раз для разных выборок и вычислить среднее из всех этих примеров по формуле среднего для нормального распределения.

Выводы

Повторим ключевые выводы урока:

• Распределение – это связка между значением переменной и вероятностью встретить это значение
• Самые распространенные виды распределений – это нормальное, равномерное и биномиальное
• Центральная предельная теорема утверждает, что сумма большого числа случайных независимых величин приближается к нормальному распределению

Дополнительные материалы

1. Нормально разбираемся в нормальном распределении
2. Равномерное распределение непрерывной случайной величины
3. Биномиальное распределение вероятностей
4. Таблица нормального распределения