Теория множеств — JS: Массивы

Теория множеств – крайне важная математическая концепция для любых разработчиков. Данные, с которыми работают программы, часто представляются как множества — значит, к ним применимы правила теории множеств. В первую очередь это касается различных операций над множествами, например, пересечения или объединения.

Это не значит, что нужно знать эту теорию от и до. Напротив, достаточно изучить ее основные понятия и некоторые операции. Этого хватит для эффективного решения подавляющего числа задач. Сама теория множеств относится к интуитивно понятным концепциям. Она хорошо ложится на здравый смысл и понятна людям даже без особой математической подготовки.

Краткая терминология

Основное понятие теории множеств, как ни удивительно — множество. Множеством обозначают набор объектов произвольной природы, который рассматривается как единое целое. Простейший пример — цифры. Множество всех цифр включает в себя 10 элементов (от 0 до 9).

Но не каждый набор объектов можно назвать множеством. Существует важное условие – все элементы множества должны быть уникальными. Например, числа 1, 1 и 3 не могут называться множеством, а 1, 3, 5 могут.

Множества между собой могут находиться в определенных отношениях. Например, множество натуральных чисел является подмножеством целых чисел, которые в свою очередь являются подмножеством рациональных чисел и так далее. Понятие «подмножество» означает, что все элементы одного множества также входят в другое множество, называемое надмножеством.

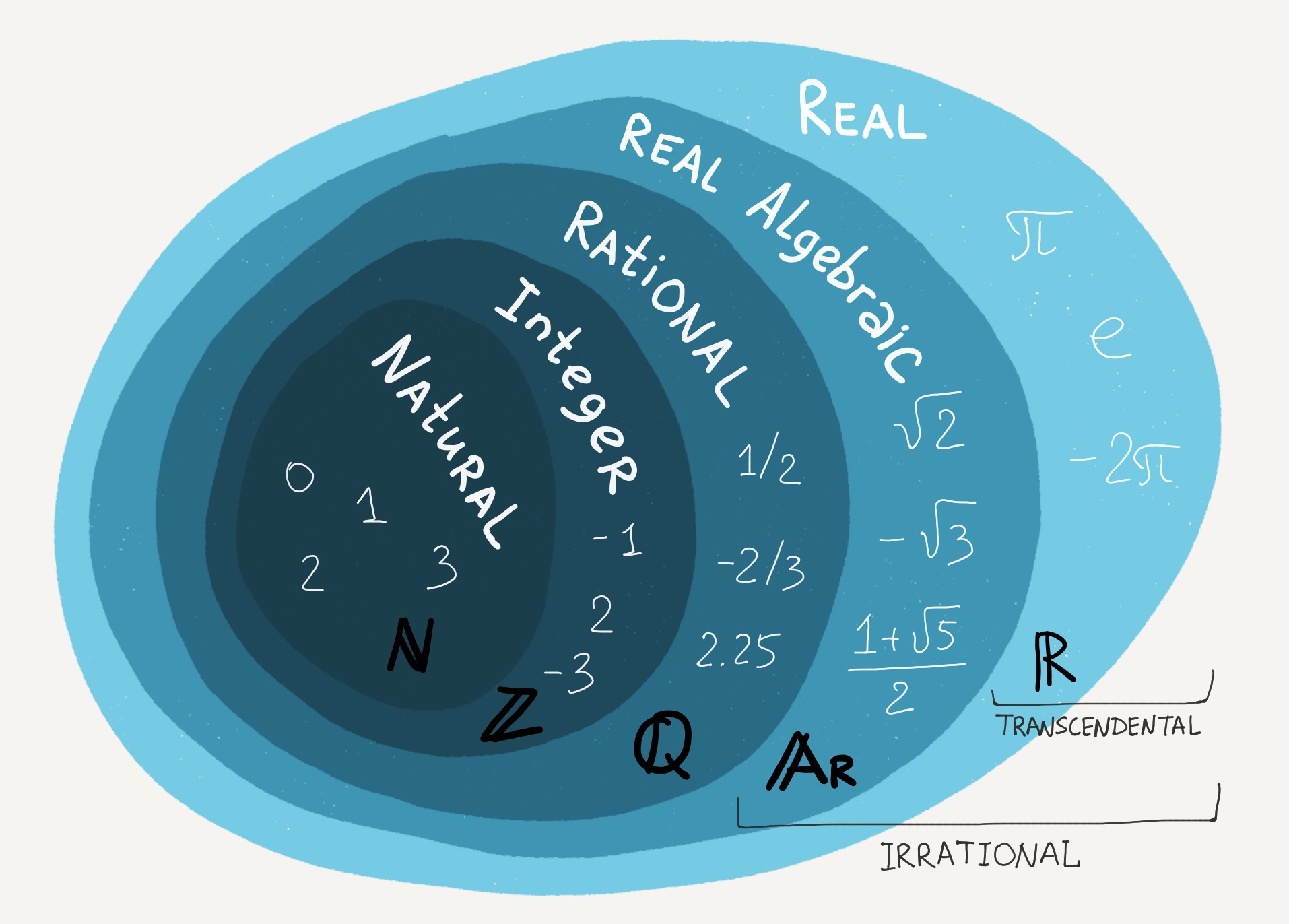
Представление множеств кружками довольно удобно. Можно быстро оценить как друг с другом соотносятся разные множества.

Но математические объекты, такие как числа, не единственные возможные объекты множеств. Множеством можно назвать группу людей, стоящих на остановке в ожидании своего автобуса, или жильцов квартир одного дома, города или страны.

В программировании в качестве множеств могут выступать массивы и таблицы в базе данных. В JavaScript для представления множеств есть встроенный механизм Set. Но для работы с ним нужно немного понимать объектно-ориентированные возможности, которые рассматриваются в более поздних курсах.

Операции над множествами

На практике представление данных в виде множеств полезно тогда, когда мы хотим что-то сделать с ними. Простой пример. Когда в Фейсбуке вы заходите на страницу другого человека, то Фейсбук показывает вам блок с общими друзьями. Если принять, что ваши друзья и друзья вашего друга — два множества, то общие друзья — множество, полученное как пересечение исходных множеств друзей.

Пересечение — один из ярких примеров операции над множествами, которая в программировании встречается повсеместно. То же самое можно сказать и о некоторых других операциях. Важно, что результатом всех этих операций являются множества, а значит они подчиняются тем же правилам, что и исходные множества. Например, сохраняется уникальность элементов.

Пересечение

Пересечением множеств называется множество, в которое входят элементы, встречающиеся во всех данных множествах одновременно.

Пример с общими друзьями:

// Друзья одного человека
const friends1 = ['vasya', 'kolya', 'petya'];

// Друзья другого человека
const friends2 = ['igor', 'petya', 'sergey', 'vasya', 'sasha'];

// Общие друзья
// Эта функция принимает любое количество массивов.
// То есть вы можете находить пересечение любого количества массивов за один вызов.
_.intersection(friends1, friends2); // ['vasya', 'petya']

Объединение

Объединением множеств называется множество, в которое входят элементы всех данных множеств.

const friends1 = ['vasya', 'kolya', 'petya'];
const friends2 = ['igor', 'petya', 'sergey', 'vasya', 'sasha'];

_.union(friends1, friends2); // ['vasya', 'kolya', 'petya', 'igor', 'sergey', 'sasha']

Каждый друг в объединении встречается ровно один раз.

Дополнение (разность)

Разностью двух множеств называется множество, в которое входят элементы первого множества, не входящие во второе. В программировании такая операция часто называется diff (разница).

const friends1 = ['vasya', 'kolya', 'petya'];
const friends2 = ['igor', 'petya', 'sergey', 'vasya', 'sasha'];

_.difference(friends1, friends2); // ['kolya']

Принадлежность множеству

Проверку принадлежности элемента множеству можно выполнить с помощью встроенного метода includes():

const terribleNumbers = [4, 13];

if (terribleNumbers.includes(10)) {
  console.log('woah!');
}

Дополнительные материалы

1. Рассказы о множествах (pdf)
2. Встроенный метод includes
3. Функция intersection из библиотеки Lodash
4. Функция union из библиотеки Lodash
5. Функция difference из библиотеки Lodash

---

Остались вопросы? Задайте их в разделе «Обсуждение»

Вам ответят команда поддержки Хекслета или другие студенты

Об обучении на Хекслете

• Статья «Как учиться и справляться с негативными мыслями»
• Статья «Ловушки обучения»
• Статья «Сложные простые задачи по программированию»
• Урок «Как эффективно учиться на Хекслете»
• Вебинар «Как самостоятельно учиться»